Фотоприемные устройства и ПЗС. Обнаружение слабых оптических сигналов
ОПТИМАЛЬНЫЙ ФИЛЬТР (АНАЛИЗ В ЧАСТОТНОЙ ФОРМЕ)
Целевая функция разработчика ФПУ определена — это максимизация отношения сигнал-шум Ыс/т на выходе канала {усилителя). Запишем выражение для отношения №с/т на выходе усилителя и будем искать его максимум по всем входящим в него параметрам.
Расчет отношения сигнал-шум на выходе усилителя. Сигнал и шум на входе усилителя были описаны генераторами токов (2.10), (2.11), (2.137):
/с(/)=5£с0-=5£сд2?'*Єо(О, (3.25)
(3.26)
Зная эти входные спектры, частотную характеристику коэффициента передачи усилителя К21 (/) (§ 1.3), можно рассчитать спектры сигнала и шума на выходе усилителя:
|
(3.27) (3.28) |
![]() У«(/)-Х.5£оа27,с4(/)єо(0,
У«(/)-Х.5£оа27,с4(/)єо(0,
Здесь ввели относительную частотную характеристику усилителя пронормировав коэффициент КгЛ!) к его максимальному значению (значение в области плато) К0г так что К21 {!) —К0к(1). Отметим, что коэффициент кЦ) безразмерен, а коэффициент /Со имеет размерность сопротивления, так как на входе усилителя оперируем токами, а на его выходе — напряжениями. Однако в ряде случаев удобней регистрировать на выходе линейного тракта и другие электрические величины: например, в накопителе удобней рассматривать заряд и размерность коэффициента должна уточняться (§ 4.5).
Нас интересует значение сигнала в тот момент времени, когда он достигает максимума; складывая все гармоники, получаем
|
00
ХС05(©*мЧ-^ + ^)**/. |
Здесь “фс, 1ру— фазочастотные характеристики сигнала и усилителя соответственно. Из этого выражения видно, что сигнал достигает максимума, когда все гармоники действуют в фазе и их амплитуды складываются. Следовательно, в момент /м к0* синусоиды под интегралом достигают своего максимального значения (единицы); следовательно, должно выполняться условие
Первое слагаемое —<»£м появляется в спектре тогда, когда импульс сдвинут по оси времени на величину гм (§ 2.1). Для радиотехники такое преобразование сигнала является стандартным: в усилитель может быть встроена линия задержки с произвольным временем задержки /м, она не изменяет ни формы сигнала, ни его амплитуды и не может повлиять на искомое отношение Л^с/ш. Принципиальное значение имеет второй член —11)0'- при импульсе несимметричной формы, когда (см> § 2.1), усилитель обязан скомпенсировать фазовое рассогласование гармоник сигнала, тогда они в момент £м дружно складываются и именно тогда сигнал достигает своего максимально возможного значения:
Со
Иск=К^ЕсА2Т^к(/)ес(/)4/. (3.31)
О
Выборки выходного шума во все моменты времени одинаковы и равны среднеквадратичному значению
|
|
= у К#2Ч1Ш у АЧЛ ® (/) <*/■ (3.32)
О
И для отношения сигнал-шум в момент получаем
2ГС 1 *(/) «с (/)<*/
И* V2?/ш, Л?
* о
Постановка задачи оптимальной фильтрации. Нет нужды комментировать очевидную зависимость отношения Ыс/Ш от таких параметров ФП и ФПУ, как чувствительность 5 и плотность шума 2ц1т. Само собой разумеется, что надо повышать 5 и снижать 1Ш. Достижимые значения 5, /ш подробно рассматривались в § 1.2, 2.5. Было показано, что в современных ФПУ эти значения близки к предельным. Нет I ,жды анализировать зависимость Мс/т от амплитуды /?са*. как в любой линейной системе, выходной сигнал и отношение Л^с/Ш линейно растут с ростом входного. Естественно, задача разработчика ФПУ — получить требуемое значение Л/сдп при минимально возможной амплитуде оптического сигнала Еса. Другие параметры сигнала, входящие в (3.32), — его длительность Тс и спектр ес{!) — задаются разработчику ФПУ. В нашем распоряжении остается
только одна степень свободы — выбор относительной частотной характеристики усилителя £(/)• Перепишем выражение для отношения сигнал'шум (3.33) в следующем виде:
|
О |
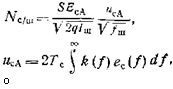 (3.34)
(3.34)
|
Со О |
![]() (3.35)
(3.35)
(3.36)
Здесь исА — относительная амплитуда выходного сигнала; /ш — эффективная полоса входного шума. Физический смысл введенных параметров понятен из их определения (3.35), (3.36). Так, относительная амплитуда исА определяется инерционностью усилителя: если он широкополосный, &(/) = 1, то спектр сигнала не искажается:
Со
|
(3.37) |
![]() ЙсА = 2ТС 5 е, (/) а/ = 2Т с - I.
ЙсА = 2ТС 5 е, (/) а/ = 2Т с - I.
О
Напомним, что интеграл здесь определяет эффективную полосу спектра сигнала (2.15). Если же полоса усилителя сопоставима с полосой спектра сигнала, то надо учитывать частотную зависимость усиления к ([)<.! и, как следует из (3.35), амплитуда выходного сигнала «заваливается» из-за инерционности усилителя (ЫСА<1).
Полоса /ш уже использовалась нами при расчете частоты ложных тревог (см. § 3.1). Напомним, что при белом шуме (0=1) формула (3.36) является общепринятым определением эффективной шумовой полосы усилителя. При таком пояснении^ становится ПОНЯТНЫМ физический СМЫСЛ множителя Мел/ ШЫ В (3.34): это отношение относительной амплитуды к квадратному корню из эффективной шумовой полосы. При очень широкой полосе усилителя, когда £(/) = 1, растет сигнал (Мса“*-!)» но увеличивается и шумовая полоса /ш, и, следовательно, шум. При узкой полосе усилителя выходные шумы падают, но падает и г^одной сигнал (Мса<С1). Можно ожидать (и это будет понятно ниже), что отношение N а/щ достигает максимума при некоторой оптимальной полосе усилителя, точнее, при оптимальной частотной характеристике &(/).
Таким образом, максимизация Ыс/Ш свелась к выбору оптимальной функции к(1). Приходим к основной задаче теории обнаружения— задаче оптимальной фильтрации. Термин «фильтрация» точно отражает поставленную задачу: надо выбрать именно фильтр, его относительную частотную характеристику
К О) Сама абсолютная величина коэффициента передачи' Ко для обнаружения не имеет значения и в формулу для Агс/ш не входит: с ростом Ко в равной степени увеличивается и сигнал, и шум, так что их отношение остается постоянным. Конечно, величина Ко должна быть достаточно большой, такой, чтобы не влияли помехи на выходе и обеспечивался необходимый уровень сигнала для срабатывания порогового устройства.
Отметим, что сопротивление и емкость входа ФПУ одновременно влияют и на шум /ш, и на частотную характеристику £(/). Параметры входной цепи надо выбирать прежде всего из условия минимального шума (§ 2.5), а требуемую характеристику формировать последующими каскадами, при необходимости используя частотную коррекцию, в том числе и обратные
Связи (см. § 1.3).
Оптимальный фильтр в случае белого шума. Найдем частотную характеристику оптимального фильтра по методике «от простого — к сложному». Начнем с простейших спектров сигнала и шума, переходя постепенно к более сложным, вплоть до произвольно заданных. Простейший случай представлен на рис. 3.5: спектр шума белый, сигнал гармонический частоты /ь точнее, почти гармонический — с постоянной спектральной плотностью в узкой полосе (Д/с<СА)- Естественно, усиление должно быть на частоте сигнала /1. Если полоса усилителя узкая, Д/у-СД/с (рис. 3.5, а, в), то получим
Д/,<д/с, ЛГСШ)~<*>”УЩ - (3.38)
Т /ш V *1 Д/у
Поскольку сигнал на выходе фильтра растет пропорционально Д/у, а шум —пропорционально у д/у, то их отношение увеличивается как УД/у до тех пор, пока полоса усилителя не превысит полосу сигнала. При Д/У>Д/С сигнал уже не растет с ростом полосы усилителя, а возрастает только шум, поэтому отношение Л7С/Ш уменьшается. Отсюда следует, что полосы надо выбирать равными, Д/У=Д/С (рис. 3.5, г, д).
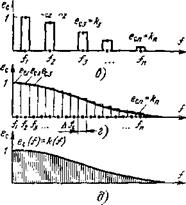
Усложним задачу; дополним спектр сигнала второй часто - т°й /2, так что он теперь состоит из двух узких — пусть равных — полос Д/с на частотах /1 и /2 разной спектральной плотности есЬ ес2 (рис. 3.6, а, б). Рассуждая по аналогии с первым случаем, находим, что полоса усиления должна соответствовать полосе сигнала Д/У = Д/С. Обозначая коэффициенты усиления на частотах и /2 соответственно к и £2, получаем
А 1^01 А/у "Ь ^2^С2 А/У 1+&г£с2
У-м2гд/у УШ?
Так как &([) и ес(/)—относительные характеристики, то для простоты расчетов их значения на частоте /1 выбраны единич-
|
/ ь |
|
І? С/ - к; У, |
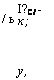 |
|
|
|
|
|
|
|
|
|
|
|
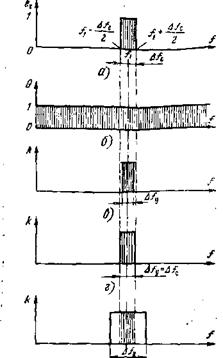
А—спектр почти гармонического сигнала; , б—спектр белого шума; в — узкая поло
Ва усилителя; е — оптимальная полоса усилителя; д — широкая полоса усилителя
Ными, &1 = 1, ес1=1. Найдем производную от полученного отношения (ее числитель):
|
(3.40) |
Ёкг Єс2 У 1 + &22 — (1 + &2ЄС2)
Простой подстановкой нетрудно проверить, что производная *ДОс/ш/<&2 обращается в нуль при к%=ес2. Таким образом,
^1 = еС1 = 1, к2 = еС2. (3.41)
|
І |
![]() Эта простая выкладка позволяет сделать важный вывод: оптимальный фильтр — такой, при котором отношение Л^с/ш минимизируется — существует. Усиление на частоте такого оптимального фильтра пропорционально спектральной плотности сигнала еС2 на этой частоте.
Эта простая выкладка позволяет сделать важный вывод: оптимальный фильтр — такой, при котором отношение Л^с/ш минимизируется — существует. Усиление на частоте такого оптимального фильтра пропорционально спектральной плотности сигнала еС2 на этой частоте.
И опять усложним задачу — рассмотрим спектр сигнала, который содержит не две, а п узких равных полос Д^с на частотах /ь 12, Н’ • ■ • ' ^п со спектральными плотностями еси е? с2,
£сз> • • • > (рис. 3.6, в). По аналогии с (3.41) можно ожидать,
Что усиление на каждой частоте должно быть пропорционально спектральной плотности сигнала:
= £С], ^2 = &3~ ^сЗ> ■ ■ * 1 К — 6сп - (3.42)
И действительно, обобщив уравнение (3.39) на рассматриваемый случай:
|
«а^са "г Л'зесз т ^оч А, ь а 5 fc~. ' —г"----- ’ (3-43) |
![]() ^ "I - ^г^са "Ь ^з^сз
^ "I - ^г^са "Ь ^з^сз
У & “Г А а2 — . . . кп
|
DNc |
![]() И найдя частные производные
И найдя частные производные
|
I ш |
![]() ^Et„Vk^+k^ + k^+.. . kj -
^Et„Vk^+k^ + k^+.. . kj -
Dkn
— (^l^cl 4'^2^с2Ч_^З^сзЧ_ • • •
У. kn - —. (3.44)
У kS + k^ + k* + .,.kn>
Видим, что они обращаются в нуль при выполнении условия (3.42).
Выражения (3.42) практически уже представляют собой, частотную характеристику оптимального фильтра для сигнала произвольной формы. Пусть задан произвольный спектр ec(f). Его можно аппроксимировать рассмотренным «полосатым» спектром, состоящим из п полос (рис. 3.6,г). При n-*-оо, Afc->-О «полосатый» спектр в пределе совпадает с заданным спектром ec(f) (рис, 3.6, д), так что формулы (3.42) в пределе (при п^оо и Л/с-^0) приводят к выражению
K(f) = ec(f). (3.45)
Полученная теорема относится к числу основных теорем теории обнаружения. Она удивительно проста: при белом шуме относительная амплитудно-частотная х а р а к ' теристика оптимального фильтра полностью повторяет относительный амплитудный спектр сигнала. Действительно, зачем усиливать на тех частотах, где нет сигнала, ведь здесь можно усилить только шум, поэтому в этой области частот £(П=ес(/)=0. На частотах, где больше спектральная плотность сигнала, должно быть и выше усиление. Теорема представляется совершенно очевидной. Но такое понимание пришло после публикации в 1943 г. Нортом работы по оптимальной фильтрации [77]. В те годы теория оптимальной фильтрации интенсивно развивалась применительно к задачам радиолокации. Позднее она была использована и для обнаружения оптических сигналов.
/И/-!-
|
Kn - |
![]()
|
Ve |
![]() &Г ~
&Г ~
VW
|
Ve |
![]() Et(/) —
Et(/) —
|
0(f) |
![]() 8kf~1
8kf~1
Рис. 3.7, К выводу частотной характеристики оптимального фильтра при произвольном спектре шума
Оптимальный фильтр в случае небелого шума. Полученная теорема легко обобщается для небелого шума. Для этого было предложено использовать такой остроумный прием — разделить усилитель на два последовательных каскада с усилением kj и Ап соответственно (рис. 3.7). Затем коэффициент усиления первого каскада fei подбирается так, чтобы «выбелить» шум на его выходе. Для этого надо положить Аг= 1/у Щ/)~, тогда ©(/) k = . Теперь на выходе первого каскада имеем белый шум и спектр сигнала ec(f)k (/)^ec(/)/V ©(/) • Но при белом шуме правило выбора оптимального фильтра нами только что получено. Пусть таким фильтром будет второй каскад — его частотная характеристика должна в точности повторять спектр сигнала на его входе, кц = ес(f)/V&(f) Обш, ее усиление двух каскадов
K(f) = kkn^- ,-L___ (3.46)
V 0(0 veto
Таким образом, получен коэффициент передачи оптимального фильтра при произвольных спектрах сигнала и шума. Физическая интерпретация модифицированной формулы для оптимального фильтра также проста: на тех частотах, где шумы
Больше, их надо подавлять, понижая усиление, хотя бы и за счет снижения сигнала.
Часто для коэффициента передачи используют запись в комплексной форме. С учетом полученных выражений для модуля (3.46) и фазы (3.30) можно записать [78]
К2] = ДГ21 ехр Уфу -|- /Со exp ( — /(цtu — Уфс) —
= /Со ехр ( — ехр (— Уфс),
К2]~ес* (/)/©(/). (3.47)
Последнее выражение говорит о том, что комплексная частотная характеристика оптимального фильтра с точностью Д° постоянного множителя (постоянного по модулю) равна комплексно-сопряженному спектру сигнала, деленному на спектр шума.
Подведем итог. Существует такая частотная характерИстика УСН-,ИТ01Я__ оптимального фильтра, при которой отношение сигна^щ максимально При белом шуме частотная характеристика оптимального <Ь ностью до множителя повторяет спектр сигнала (при неси им Т^а с т°ч" ле указанные характеристики комплексно-сопряжены) МетРичном сигна - спектре шума 0(/) частотная характеристика оптималнього^фи^ь011380^1101* нительно уменьшается на каждой частоте обратно пропорционально*©^'.