КОСМИЧЕСКИЙ КОРАБЛЬ ЧТО НАДО ПРЕОДОЛЕТЬ
|
З |
Емля — одна из девяти больших планет солнечной системы. С огромной скоростью мчится она в безвоздушном пространстве по своей почти круговой орбите вокруг Солнца на расстоянии около 150 миллионов километров от него. Это расстояние принимают за одну астрономическую единицу.
Приблизительно в плоскости этой же орбиты движутся и остальные восемь больших планет, а также большое количество малых планет—астероидов.
Межпланетное пространство ограничивается орбитой самой отдалённой планеты — Плутона, находящейся от Солнца на расстоянии около шести миллиардов километров. В этом безбрежном пространстве, преодолевая или используя могучее солнечное притяжение, минуя блуждающие метеорные тела и рои астероидов, и должны будут проложить свои пути межпланетные корабли.
Что мешает нам осуществить полёт в мировое пространство?
Прежде всего сила тяготения. Всё, находящееся на Земле, притягивается к её центру. Но не только Земля, а любое тело — мельчайшая песчинка и звезда-гигант — обладает этим свойством материи, которое мы называем силой тяготения. Все окружающие нас предметы притягивают друг друга, хотя мы этого не замечаем из-за ничтожной величины притягивающих сил. Сила же притяжения земного шара постоянно нами ощущается.
Если бы не было силы тяготения, все предметы улетели бы с Земли в мировое пространство, Земля удалилась бы бесконечно далеко от Солнца, а Луна от Земли. Сила притяжения затрудняет и космический полёт.
Может ли ракета оторваться от Земли и больше не упасть на её поверхность?
Да,, может. Представьте себе, что на горе, достигающей такой высоты, где воздух уже не препятствует движению ракеты, сооружена горизонтальная пусковая площадка (рис. 1). С этой площадки с определённой скоростью стартует ракета. Описав крутую дугу, она упадёт на некотором расстоянии от горы. Увеличим скорость и дальность полёта вдвое — траектория, по которой полетит ракета, окажется более пологой. Наконец, ракете можно сообщить и такую скорость, при которой кривизна
|
Рис. 1. С увеличением скорости увеличивается дальность полета ракеты и уменьшается кривизна её пути. Достигнув круговой скорости ^верхняя орбита), ракета летит параллельно поверхности Земли и становится её спутником. |
Её траектории будет равна кривизне поверхности Земли. В этом случае ракета облетит Землю кругом и вновь отправится в полёт вокруг неё. Подобно Луне, она станет спутником нашей планеты и никогда не упадёт на её поверхность.
Наименьшая скорость, при которой тело начнёт двигаться вокруг Земли, не падая на её поверхность, называется первой астронавтической или круговой скоростью.
Почему же при такой скорости тело не падает на Землю?
Когда самолёт облетает Землю по экватору или меридиану, то на него действует центробежная сила, которая тем больше, чем выше скорость. Эта сила направлена обратно силе тяжести, она стремится оторвать самолёт от Земли. При небольших скоростях центробежная сила почти незаметна, но при скорости 7Г9 километра в секунду она становится рамой силе тяжести и уравновешивает её. Это и есть первая астронавтическая скорость. Если бы не было сопротивления воздуха, то самолёт, достигший такой скорости, вращался бы беспрерывно вокруг Земли при выключенном двигателе. Он превратился бы в искусственный спутник Земли.
А какой скоростью должно обладать тело, чтобы преодолеть земное притяжение и улететь в мировое пространство?
|
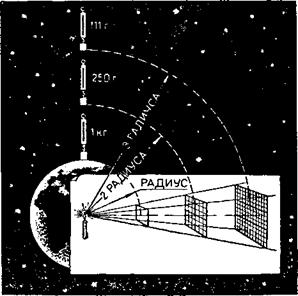
Рис. 2. Притяжение Земли уменьшается с расстоянием так же, как освещённость предметов по мере их удаления от источника света. |
Чтобы ответить на этот вопрос, мы должны ближе познакомиться с действием силы тяготения.
Сила притяжения Земли, как и других небесных тел, по мере удаления от её центра уменьшается. Она ослабевает так же быстро, как освещённость предмета по мере удаления источника света, то есть обратно пропорционально квадрату расстояния (рис. 2). Другими словами, на расстоянии, вдвое большем от центра Земли, сила притяжения в четыре раза меньше, на расстоянии, в три раза большем, она в девять раз меньше и т. д.
Чтобы освободить тело от притяжения планеты, необходимо выполнить такую же работу, как для его подъёма на высоту, равную радиусу планеты, если допустить, что сила тяжести не меняется по мере удаления тела от центра планеты. Это количество энергии можно сообщить телу, придав ему определённую скорость вблизи поверхности Земли. Обладая такой скоростью, тело двигалось бы по ветви параболы (рис. 3). Отсюда — название этой скорости: параболическая с к о -
Р о с т ь, или вторая астронавтическая скорость; часто её называют ещё «скоростьюусколь - з а н и я». На поверхности Земли эта скорость равна
11,2 километра в секунду.
Если телу сообщить скорость больше круговой, но меньше параболической, то оно начнёт двигаться по эллиптической орбите. Если же скорость больше параболической, то тело будет двигаться по ветви гиперболы (рис. 3).
Для простоты мы считали, что тело находится под действием силы притяжения одной Земли. В действительности на него действует сила притяжения Солнца. Расчёты показывают, что для того, чтобы одновременно освободить тело от притяжения Земли и Солнца, следует сообщить ему скорость не меньше чем 16,7 километра в секунду. Это — третья астронавтическая скорость.
Достигнуть первой, второй и третьей астронавтических скоростей — задача астронавтики.