Переходные процессы электропривода с линейной механической характеристикой при Мс=f(w)
В случае линейной М от w, т. е. при Мс=кw дифференциальное уравнение, определяющее переходный процесс, имеет вид
, где
Wy - скорость установившегося режима при Мс=Мy,
Dwy - падение скорости при установившемся режиме.
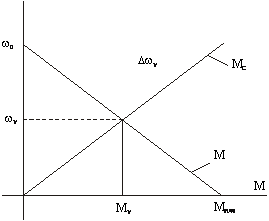Учитывая, что wy+Dwy=w0 и умножая обе части уравнения на 
, получим
Откуда 
,где 
Решение этого уравнения относительно w и М дает законы изменения w, М и I
; 
Длительность переходного процесса 
Т`м - это время, за которое электропривод разгонится из неподвижного состояния до wy при постоянном Мпуск.
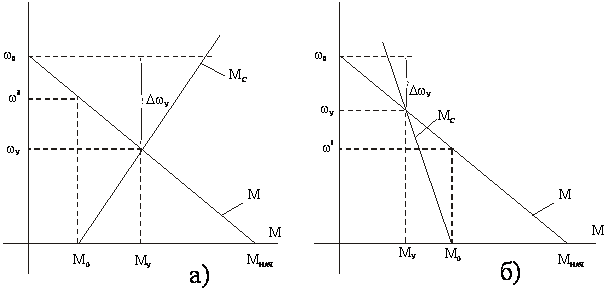
При Мс=М0+К1w (рис.”a”) и Мс=М0-К1w (рис.”б”) переходный процесс описывается этими же уравнениями, что и при Мс=Кw, но в них 
При вентиляторном моменте сопротивления дифференциальное уравнение, отражающее переходный процесс, имеет вид
Хотя это уравнение решить можно, однако конечные результаты мало пригодны для практического использования. Поэтому на практике чаще используются графические и графоаналитические методы. Естественно, что такие методы дают лишь приближенные результаты, однако, при тщательном выполнении их точность достаточна для решения практических задач. Правда, такие методы имеют и такой недостаток: они не дают возможности получить общие выводы. Решение может быть найдено лишь для отдельных частных случаев, когда значения всех параметров электропривода известны. Рассмотрим некоторые из них.
