ПРОМЫШЛЕННАЯ ТЕПЛОПЕРЕДАЧА ТЕОРИЯ И ЕЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ. ОСНОВНЫЕ ЧИСЛОВЫЕ ПРИМЕРЫ

Теплоотдача в насадке регенератора 0

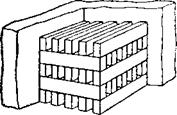
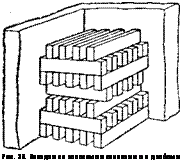
В насадке регенераторов различают шахматное и коридорное расположение кирпичей (рис. 35). При коридорном расположе­нии (гладкая канальная усадка) образуются каналы, проходя­
щие сверху вниз и в горизонтальной плоскости. В двойной шах­матной насадке, напротив, не существует сквозных каналов: кирпичи. положены «на просвет», так что газ, как и в трубном пучке с шахматным расположением, после прохода между двумя кирпичами каждый раз встречает на своем пути другой кирпич.

Теплоотдача в шахматной и коридорной насадках (шахматная и коридорная решетчатая уклад­ка) и тепловые потоки в кирпиче были исследованы Г. Кистнером [116] и К. Шумахером [117],[118]. В соот­ветствии с этими исследованиями коэффициент теплоотдачи кон­векцией от воздуха и отходящего газа к коридорной насадке

А = 7,5 —— ккал/м2 • час • °С.

У7

(354)

Опыты показали, что коэффици­ент теплоотдачи в двойной шах­матной насадке на 16% выше, чем в коридорной. Следователь­но, коэффициент теплоотдачи кон­векцией в двойной шахматной на­садке

А = 8,6 —— —— ккал/м2 • час • °С.

(355)

Эта зависимость от скорости сохраняется также и в области, где поток характеризуется значениями Яе ниже критических, т. е. при (нестабилизированном) ламинарном движении.

В этой формуле не отражено влияние температуры газа. При­чина в том, что в опытах не было очень больших изменений тем­пературы и, ка<к известно, влияние температуры на коэффициент теплоотдачи конвекцией было не очень велико. Средняя темпе­ратура газа и воздуха держалась на уровне 700° С, т. е. при­мерно 1000° К. Так как изменение коэффициента теплоотдачи

Происходит примерно пропорционально корню четвертой степени из абсолютной температуры, то в уравнения (354) и (355) необ-

4 Г Т

Ходимо ввести фактор [119]І/ В случае Т = 1000° этот фактор

Равен 1, следовательно, уравнения (354) и (355) дают правиль­ные значения. Таким образом, скорректированная формула для коэффициента теплоотдачи конвекцией от воздуха и отходящего газа к насадке с решеткой со сквозными каналами примет вид

Ос = 7,5- —— і / —-— ккал/м2 • час • °С (354а)

Yd 1000

И для шахматной укладки решетки

А = 8,6 • w°.......... і / —— ккал/м2 • час • °С. (355а)

У 1000

Чтобы рассчитать теплоотдачу для других, отличных от воз­духа и дымовых газов, целесообразно пользоваться коэффици­ентами сравнения, которые даны в среднем столбце табл. 12 на стр. 196 в расчете для трубного пучка (числовой пример см. на стр. 465).

Г. Теплоотдача от перегретого пара в трубе

Общее уравнение для теплоотдачи в трубе [уравнение (260), стр. 151], судя по его выводу, справедливо и для перегретого пара.

В то время как более ранние измерения теплоотдачи от водя­ного пара не вполне удовлетворительны, известные на сегодня новые исследования дают возможность дополнительной провер­ки формулы опытом. В. Г. Мак Адамс, В - Е. Кеннель и Дж. Н. Аддомс * исследовали теплоотдачу конвекцией в коль­цевом пространстве, которое было образовано двумя концен - трично расположенными трубами. Наружный диаметр внутрен­ней трубы составлял 6,4 мм, а внутренний диаметр наружной трубы 9,7 мм, так что кольцевое пространство имело зазор в 1,6 мм. Длина измерительного участка составляла 3,1 м. Следо­вательно, речь идет об исследованиях, проводимых при очень маленьком гидравлическом диаметре. При определении такого

Малого поперечного сечения кольца путем вычитания двух диа­метров неизбежно должны получаться неточности, особенна, если в расчете указано, что внешняя яеобогреваемая стенка также принимает некоторое участие в теплообмене вследствие луче­испускания. Но при этом изменяется гидравлический диаметр, так как он зависит от процесса теплообмена (см. определение гидравлического диаметра на стр. 177).

С учетом этой маленькой оговорки ниже анализируются ре­зультаты работы, которая, наконец, дала возможность измерить коэффициент теплоотдачи конвекцией при очень высоких давле­ниях и скоростях.

Применяемые давления доходили до 246 ага, скорости (0° С, 760 мм рт. ст.) — от 92,5 до 300 м/сек, температура пара — до 540° С и температура стенки — до 700° С.

Конечная формула имеет вид:

А = - у • 0,0214 • ^1 + Re0’8 X

X Рг1/3 ккал/м2 • час • °С. (356)

В этом уравнении:

1 + 2,3 --- выражение, учитывающее влияние длины (см.

Стр. 167);

Re—число Рейнольдса (см. стр. 115);

Ё*- п

Рг— критерий Прандтля (3600- с-g - г])/А, (см. стр. 116) ; d — диаметр трубы в свету, м

Ь — длина трубы, по которой движется исток, м.

Формула заимствована из приложения к работе, которая бы­ла написана прежде, чем авторам 'стали известны результаты измерений коэффициента теплопроводности Кейеса и Санделла (см. стр - 153, 154, рис. 19 и 20). Вследствие этого оказалось необ­ходимым выведенную прежде формулу полностью перестроить и изменить не только постоянные перед формулой, но и показа­тели степени для критериев, т. е. для скорости и диаметра.

Однако коэффициенты теплопроводности, найденные Кейесом и Санделлем для экстраполированной температурной области, т. е. выше 350° С, нельзя рассматривать как окончательные. Они также отклоняются от значений, полученных Тимротом и Вар - гафтиком, нанесенных вместе с величинами Мак Адамса, Кен - нелля и Аддомса на рис. 9 (до соотношения 1 : 1,6 при 600° С), и имеют в некоторой степени диаметральф противоположную тенденцию изменения в зависимости от температуры, что не мо­жет свидетельствовать о надежности значений коэффициентов теплопроводности при температурах выше 300° С.

При этих обстоятельствах применение безразмерных Крите - ' риев для обобщения измеренных значений нужно считать не­удачным. Так как по этой причине непосредственно измеренные значения в этой полноценной работе не указываются, а даются лишь в пересчете с ненадежными коэффициентами теплопровод­ности, то на основе этого трудно вывести эмпирическую фор­мулу, которая в ранее приведенном виде дает коэффициент теп­лоотдачи пара как функцию скорости, диаметра, температуры и в известных условиях давления. На основе подобной эмпириче­ской формулы или измеренных значений можно было бы затем, пользуясь методом, указанным на стр. 142—151, вывести общую формулу теор™ подобия, если коэффициенты теплопроводности установлены окончательно.

Если теперь перейти к сравнению формулы (356) с уравне­нием (260), то прежде всего снова обнаруживается различие в показателях степени для члена ы)*у9 т. е. 0,8 или 0,75 (крите­рий Яе содержит хю-у или т0-уо (см. стр. 89), следовательно, Яе пропорционально (ДОо'Уо)71]* Однако более подробное рас­смотрение окончательной кривой в общем представлении ре­зультатов исследования на рис. 10 показывает, что результаты описываются лучше, если с соответствующим измененным коэф­фициентом вместо Яе0,8 взять Яе°'7Ь% Тогда видно, что кривая, характеризуемая Яе0,8, при высоких числах Рейнольдса (выше Яе = 25000) отчетливо лежит на верхней границе области до­вольно разбросанных точек измерения, в то время как по отно­шению к измененной кривой, характеризуемой Яе0,7*> эти точки ложатся лучше, а при малых значениях Яе — достаточно хорошо.

Следовательно, эти измерения говорят о том, что. показатель степени для скорости 0,75, найденный автором выше (см. стр. 142), правильнее, чем 0,8. Однако разница между этими по­казателями так мала, что она отчетливо выявляется лишь при значениях числа Рейнольдса, превышающих 30000.

Расчет некоторых числовых примеров по уравнениям (260) и (356) показывает, что расхождение между обеими формулами лежит в пределах погрешности, обусловленной точностью опре­деления физических параметров веществ. Величину вязкости, сильно влияющую на величину числа Рейнольдса, следует рас­считывать для широкой области по формуле Сутерланда, так как измеренных значений нет. 1

В качестве числового примера необходимо привести следую*« щий:

При гю0 = 100 м/сек - й = 0,03 м I = 400° С; а по (260) равен 366 ккал/м2:час*°С; а по (356) равен 320 ккал/м2*час>° С; при т0 = 40 м/сек (I = 0,02 м ^ = 300° С; .

А по (260) равен 192 ккал/м2 • час -°С; а по (356) равен 186 ккал/м2 • час *°С.

Для значений а из уравнения (356) и рис. 9 обсуждаемой здесь работы легко можно определить значения коэффициентов теплопроводности, которые приводят к точному совпадению обо­их уравнений. Следовательно, уравнение (267) пока что спра­ведливо и для водяного пара:

( І юп’75

А = I 3,8 + 0,26---------- 1---------- ккал/м?1 • час • °С.

I Юо а°’25

Так как это уравнение выведено из уравнения (260), то косвен - но можно доказать, что уравнение (260)

0У°’75

А =19,3 • с2’81 • X0,91 —----- --- ккал/м2 • час - °С

*0.25

Справедливо не только для всех газов, что уже доказано, но и для всех перегретых паров.

Как известно, законы для газов с достаточной точностью при­менимы и к перегретому пару, следовательно, по газовым зако­нам можно рассчитать скорость гю0 при нормальных условиях (0°С, 760 мм рт. ст.). Естественно, для пара при температуре 0° это носит условный характер. Если известны истинная ско­рость пара т м/сек, давление р кг/см2 и температура /°С, то скорость пара при нормальных условиях

Су0 = су • —64 -- р - м/сек. (357)

273 + * 4 '

Еще проще определить скорость т по количеству пара й кг/сек, которое протекает по трубе за секунду. Если поперечное сече­ние трубы в свету ж2, то справедливо соотношение

В = Т7 • иу0 • То к?/сек.

При у ==: 0,804 искомая скорость

А»0 = 1,24------ м/сек (358)

Г

Или, относя к диаметру,

И»0= 1,58 ----- м/сек. (358а)

Й*

Изложенное в этом разделе относится лишь к случаю, когда

Температура стенки выше температуры насыщения пара. Если

Температура стенки ниже этой температуры, то он конденси­руется на стенке, что вызывает значительное повышение тепло­передачи. По опытам Якоба и Эрка теплоотдача от конденси­рующегося перегротого пара в общем превышает теплоотдачу от конденсирующегося насыщенного пара одинакового давле­ния.