ШИНЫ. НЕКОТОРЫЕ ПРОБЛЕМЫ ЭКСПЛУАТАЦИИ И ПРОИЗВОДСТВА
Методы разработки новых конструкций шин
Вот уже на протяжении многих десятилетий наиболее полно и систематически вопросами разработки новых конструк
Ций шин занимались и занимаются ведущие специалисты НИ - ИШПа: Бидерман В. П., Бухин Б. П., Соколов С. Д., Басс Ю. П. и др.
Вначале проектирования разработчик должен поставить и ответить на следующие вопросы [486]: 1) какие характеристики должна иметь сконструированная шина; 2) как будут изменяться эти характеристики, если изменить ее конструкцию, материалы, условия нагружения и т. д.; 3) какие эксплуатационные свойства будет иметь машина с конкретными шинами; 4) какие характеристики должна иметь шина, чтобы машина имела требуемые эксплуатационные свойства; 5) какими должны быть конструкция и материалы шин, чтобы последняя обладала требуемыми эксплуатационными свойствами; 6) как создать оптимальную конструкцию.
Расчетно-экспериментальный метод разработки шин имеет следующую логическую цепочку: задание конструкции шины
- физическая модель (расчетная схема) - математическая модель
- решение и получение численных результатов - проверка адекватности - настройка модели - практическое опробование шины.
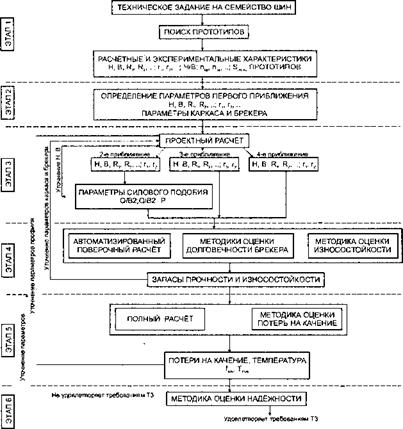
В наиболее подробном варианте схема разработки конструкции шины и оценки ее работоспособности приведена в [487], (рис. 60).
В данной схеме МКЭ обозначает «метод конечных элементов»; НДС - напряженно-деформированное состояние; РКК - резинокордный композит; ОКН - образец с косой нитью.
Данная схема в основных деталях повторяет вышеприведенную логическую цепочку и содержит следующие этапы: 1) выбор конструкции шины, материалов для ее изготовления, технологии изготовления и изготовление опытных образцов для расчетных данных; 2) определение НДС расчетными и экспериментальными методами; 3) определение режима вулканизации расчетными и экспериментальными методами; 4) испытания опытных шин в требуемых режимах нагружения; 5) про-
474
|
Тензометрический' |
![]()
|
Учет Влия Ния Дороги И Автомо Биля |

Выбор
Исходного
Варианта
Определение НДС изделия
Материалы
Технология
Конструкция
Расчетные
Методы
Нелинейные вязкоупругие свойства резин и РКК
Целевая
Функция
Изделия
Многослойные
Анизотропные
Оболочки
МКЭ
Эксперимен
Тальные
Методы
Определение режима вулканизации
Поляризационно
Оптическая
Расчеты тепловых потоков и температурных полей
Измерения температур в изделии при вулканизации
|
|
||
|
|||
|
|||
Квазиравновесные
|
Испытания Образцов |
![]()
|
Усталостные |
![]() Негармонические циклы
Негармонические циклы
Динамические
|
Сцепление, износ
|
Рис. 60. Схема оценки работоспособности шины.
Гнозирование ресурса шин с учетом условий эксплуатации и проверка принципа «равнопрочности»; 6) при необходимости корректировка пункта 1 и повторение цикла исследований.
Одним из главных элементов этой схемы является расчет механических характеристик шин, который включает почти все виды математического аппарата: системы линейных и нелинейных уравнений, векторный анализ, обыкновенные дифференциальные уравнения и уравнения с частными производными, краевые задачи, случайные процессы и математическая статистика, численные методы и т. п. Важным является то, что имея математическую модель можно проводить машинные эксперименты по оптимизации конструкции покрышки, по изучению влияния изменений исходных данных на характеристики шины и автомобиля. В результате расчетов можно получить следующие характеристики шины данной конструкции в зависимости от условий эксплуатации, механических и термических свойств конструкционных материалов: прочность и долговечность, сопротивление качению, выходные характеристики, материалоемкость, шум и другие экологические характеристики, ремонтопригодность.
Понятно, что "вручную" практически невозможно сделать все необходимые расчеты. По этой причине и у нас в России5и за рубежом созданы программы для расчетов на ЭВМ. С появлением мощных персональных ЭВМ в НИИШПе создан на языке "Фор - тран-77" ряд специализированных программ для компьютеров типа РС1ВМ, например, программа "АПР - ПЕРСОНАЛ" может быть использована в конструкторской практике как самостоятельно, так и в рамках разрабатываемых систем автоматизации проектирования пневматических шин - САПР - Ш. Как и предыдущие программы, данная программа с достаточной для практики точностью позволяет рассчитать основные механические характеристики шин радиальной конструкции:
1 - габариты накаченной шины;
2 - максимальные и минимальные значения напряжения в циклах нагружения корда каркаса и брекера и резины протектора;
3 - радиальный прогиб шин под нагрузкой;
4 - длину контакта с дорогой;
5 - боковую и угловую жесткости;
6 - усилия в бортовых кольцах от внутреннего давления и догрузку колец при обжатии;
7 - характеристики бокового увода;
8 - интенсивность работы трения в протекторе при качении с уводом.
В САПР - шина данная программа может быть использована в процедурах "Оптимизация напряженно-дсформированного состояния и внутреннего давления в шине", "Оценка влияния конструктивных характеристик на работу сил трения в контакте", "Оценка влияния конструктивных характеристик на боковую, угловую и крутильную жесткости", "Оценка влияния конструкции шины на характеристики бокового увода".
В рамках иерархической системы моделей шины, состоящей из 3-х этапов: определения динамической нагруженности, определения изменения геометрии и определения напряжений и деформаций элементов шины, данная программа применяется на втором этапе расчетов. Этот этап предусматривает вычисление перемещений и изменений кривизны поверхности шины, усилий в нитях корда, а также жесткостных характеристик и параметров контакта с опорной поверхностью.
САПР - шина успешно используется в НИИШПе для проектирования семейства шин [489], то есть нескольких подобных шин, образующих размерный ряд (10.00Р20, 11.00Р20, 12.00Р20). Структура САПР - шина представлена на рис. 61.
Внутри семейства должно обеспечиваться постоянство или подобие следующих параметров: рисунка протектора, типа
|
Рис. 61. Система автоматизированного проектирования шин (САПР - шина). |
|
Рис. 62. Схема проектирования семейства шин. Н - высота профиля шины; В - ширина профиля шины; - нормальная нагрузка на шину; Р - внутреннее давление в шине; пк, пбр, пбк - статические коэффициенты запаса прочности соответственно каркаса, брекера, боковых колец; 8)юл)1 - полный ресурс шины; Л,, БЦ - радиусы кривизны беговой дорожки соответственно по прессформе и по углу; г,, г2 - радиусы кривизны внутреннего профиля шины соответственно по короне и по углу. |
Шины, формы профиля, соотношений геометрически подобных профилей, конструкций каркаса и брекера, назначения по условиям эксплуатации.
Проектирование семейства шин состоит из шести этапов и начинается с разработки технического задания (рис. 62).
Дальнейший ход проектирования ясен из схемы. На 3-ем этапе в результате проектного расчёта выбранных прототипов семейства шин (третье или четвёртое приближение) уточняются параметры профиля за счёт чего улучшаются эксплуатационные характеристики шин: уменьшаются коэффициенты сопротивления качению, диапазон изменения температур (113-120 °С вместо 110-158 °С при скорости 70 км/ч и 166-177 °С вместо 161-195 °С при скорости 100-110 км/ч), суммарная удельная работа трения в зоне контакта. За счёт этого у спроектированных шин по сравнению с прототипами уменьшается интенсивность износа протектора шин и увеличивается ресурс шин по износу. Показатели прочности семейства спроектированных шин будут выше, чем у прототипов. В таблице 7.1 приведены показатели износостойкости спроектированного по предложенному методу семейства грузовых шин 10.00Р20 - 12.00Р20. В таблице 7.1 в скобках приведены аналогичные показатели для прототипов.
Если ещё раз обратиться к схеме оценки работоспособности шины, то можно увидеть, что расчётные методы можно проводить либо базируясь на представлении шины многослойной анизотропной оболочкой вращения сложной геометрии, либо разбивая шину на отдельные небольшие элементы, используя метод конечных элементов (МКЭ). Пожалуй, с появлением мощных расчётных средств, метод МКЭ можно признать более перспективным, однако возможности первого направления далеко не исчерпаны и примером этого может служить работа, проведённая конструкторским отделом ОАО "Нижнекамскшина" совместно с учёными НИИ КГШ [490] по установлению механических особенностей шин с регулируемым внутренним давлением.
Показатели износостойкости спроектированного семейства грузовых шин 10.00Р20 - 12.00Р20
|
Показатель |
10.00Р20 |
11.00Р20 |
12.00Р20 |
|
Радиальная нагрузка, Н |
26730 (26490-26730) |
26490 (28450) |
28450 (31820) |
|
Интенсивность работы трения при действии боковой нагрузки, Дж/м |
248 (246-288) |
258 (278-281) |
291 (278-288) |
|
Удельная работа трения при действии боковой нагрузки на единицу пути, кДж/м3 |
0,52 (0,6-0,51) |
0,5 (0,52-0,53) |
0,51 (0,49-0,51) |
|
Удельная работа трения при действии окружной силы на единицу пути, кДж/м3 |
1,79 (2,0-2,06) |
1,77 (2,14-2,2) |
1,8 (2,17-2,4) |
|
Суммарная удельная работа трения при действии окружной и боковой сил на единицу пути, кДж/м3 |
2,32 (2,51-2,66) |
2,27 (2,66-2,73) |
2,31 (2,66-2,91) |
|
Коэффициент сопротивления качению |
0,0041 (0,00466) |
0,0042 0,00435 (0,00449-0,0059) (0,0046-0,0053) |
|
|
Интенсивность износа в эксплуатации (дороги гр. А), мм/тыс. км |
0,08 (0,083-0,0096) |
0,1 (0,12) |
0,12 (0,14-0,16) |
|
Высота изнашиваемой части рисунка протектора, мм |
11,3 |
12,2 |
13,2 |
|
Условный ресурс шины по износу, тыс. км |
141,2 (117-136) |
122 (102) |
110 (83-94) |
Пневматические шины с регулируемым внутренним давлением эксплуатируются на многочисленных геолого-разведоч - ных, буровых и других транспортных средствах. Создание таких шин представляет собой сложную проблему, так как необходимо обеспечить высокую работоспособность и заданные выходные характеристики в широком диапазоне изменения нагрузок. Для исследования нагруженности элементов таких шин
была использована математическая модель шины, представляющая собой слоистую геометрически нелинейную моментную анизотропную оболочку подверженную одновременному действию внутреннего давления Р и внешних эксплуатационных нагрузок [491]. Расчёт напряжённо-деформированного состояния шины осуществлялся путём минимизации функционала полной энергии оболочки Э:
![]()
|
11 + ^12^12 + ^22^22 + ОГ,3Єіз + СУ23^2з) + |
![]()
|
(52) |
![]() + Эп - J (q^i + q2U2+ Яз^з) dFk, Ря
+ Эп - J (q^i + q2U2+ Яз^з) dFk, Ря
Где величины с индексами а, £, и, я - компоненты напряжений, деформаций, перемещений и интенсивности внешних нагрузок; Эп - энергия деформации протектора.
|
(53) |
![]() Э„ =~ I h„ [Е„є33 + Gn (Y! + Y2)]dFc,
Э„ =~ I h„ [Е„є33 + Gn (Y! + Y2)]dFc,
2 Fc
Где - Ь, Е, в - высота протектора, модуль упругости и сдвига материала протектора; Рк, РЧ ,РС - поверхность каркаса; площадка по которой действуют внешние нагрузки и поверхность контакта; у,, у2 - компоненты сдвиговых деформаций протекто-
Pa.
С помощью соотношений (52, 53) проанализировано напряжённо - деформированное состояние радиальной комбинированной шины диаметром 1260 мм и шириной профиля 425 мм, эксплуатирующейся при внутреннем давлении от 80 до 550 КПа и нагрузке Q, достигающей 30 КН.
При создании шины профиль её поперечного сечения был оптимизирован, а в качестве критерия оптимизации использован минимум коэффициента сопротивления качению f:
Где Р - сила сопротивления качению [492], К - гистерезис - ные потери материала; Л£т - амплитуда интенсивности деформаций, определяемая как разность интенсивностей деформаций элементов шины при нагружении внутренним давлением и внешней нагрузкой.
Д8Т= | £?- £ | (55)
Интенсивность деформации определяется по следующей зависимости
|
|
И может служить обобщённой характеристикой деформационного состояния. Оптимизация формы поперечного сечения осуществлялась методом последовательных приближений. В качестве первоначальной формы была принята классическая форма, определяемая по известным соотношениям [493], в дальнейших расчётах форма поперечного сечения корректировалась. Ниже в таблице 7.2 представлены результаты расчётов коэффициента сопротивления качению для классической и оптимальной форм профилей при нагрузке С? = 30 КН и внутреннем давлении в шине в диапазоне 80-550 КПа.
Таблица 7.2
Значения коэффициента сопротивления качению
|
Р, КПа |
80 |
120 |
200 |
450 |
550 |
|
Форма профиля: Классическая Оптимальная |
0,030 0,046 |
0,072 0,025 |
0,005 0,005 |
0,004 0,003 |
0,003 0,0025 |
Как видно из этой таблицы, классическая форма профиля имеет заметные преимущества при работе на пониженном давлении; при давлении выше 100 КПа предпочтение имеет оптимальный профиль, форма которого была близка к форме рекомендованного 11СОТ [494], однако в бортовой зоне она имела заметные отличия. Очевидно, что единой оптимальной формы профиля во всем диапазоне нагрузок быть не может, поэтому поиск её следует производить для основного режима нагружения, наиболее характерного для работы транспортного средства.
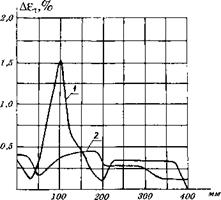
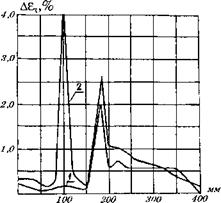
Для анализа деформационного состояния шины, на рис. 63- 66 приведены характер распределения амплитуды интенсивности деформации на наружной поверхности каркаса, а также изменения интенсивности деформации за оборот колеса для вершины шины. Кривая 1 на этих рисунках соответствует классическому профилю, а кривая 2 - оптимальному. Преимущества оптимального профиля при повышенных значениях внутреннего давления очевидны, также как и очевидно преимущество классического профиля при низком давлении. Анализируя напряжённо-деформированное состояние шины, обратим внимание на характер изменения интенсивности деформации за оборот колеса, который зависит от конструктивных факторов шины и режимов нагружения (рис. 65-66). Эти характеристики во многом определяют работоспособность шины. Дело в том, что гистерезисные потери в материале и усталостная долговечность определяются экспериментально и, как правило, при гармоническом режиме нагружения. Импульсный характер воздействия нагрузки, как видно из рис. 65-66, составляет ~ 1/6 от периода качения колеса. Известно, что величина потерь при гармоническом режиме в 1,5-2 раза меньше, чем при импульсном. К этому следует также добавить, что на величину гистерезисных потерь и на усталостную долговечность существенную роль оказывают деформации £тРо и £т°. Знание уровня напряженно-де - формированного состояния во всём диапазоне нагружений
|
Вершина Борт Рис. 63. Изменение амплитуды интенсивности деформации для наружной поверхности каркаса при давлении 550 кПа 1 - классический профиль 2- оптимальный профиль |
|
Вершина Борт Рис. 64. Изменение амплитуды интенсивности деформации для наружной поверхности каркаса при давлении 80 кПа 1 - классический профиль 2- оптимальный профиль |
|
Et,%
12 3 4 Радианы |
|
3,0 2,0 1,0 |
![]()
|
Рис. 65. Изменение интенсивности деформации за оборот колеса для вершины классического профиля шин. 1,2- внутреннее давление 80 и 550 кПА соотвественно |
|
Ет,% |
|
12 3 4 Радианы |
|
2,0 |
![]()
|
1,0 |
![]() Рис. 66. Изменение интенсивности деформации за оборот колеса для вершины оптимального профиля шин.
Рис. 66. Изменение интенсивности деформации за оборот колеса для вершины оптимального профиля шин.
1,2- внутреннее давление 80 и 550 кПА соотвественно
Шины позволяет либо сформулировать требования к создаваемым материалам, либо подобрать нужный материал, что в конечном счёте обеспечит высокую работоспособность конструкции в целом. Для демонстрации справедливости используемой математической модели на рис. 67-68 показаны расчётные и экспериментальные данные, демонстрирующие зависимость прогиба шины (рис. 67) и среднего контактного давления (рис. 68) от величины внутреннего давления в шине при постоянной нагрузке (5 = 30 КН. На этих рисунках кривая 1 соответствует эксперименту, а кривая 2 - расчёту. Совпадение данных вполне удовлетворительное, однако нужно всё же заметить, что сравниваемые величины являются интегральными характеристиками.