Двигатели стирлинга

ДВИГАТЕЛЬ С РАБОЧИМ И ВЫТЕСНИТЕЛЬНЫМ ПОРШНЯМИ (КОМПОНОВОЧНАЯ МОДИФИКАЦИЯ БЕТА)

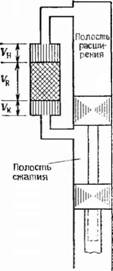
Если рабочий и вытесннтельный поршни движутся в одном цилиндре, то машину такого типа называют двигателем ком­поновочной модификации бета. Полость сжатия в подобном дви­гателе образована объемом, заключенным между нижней по­верхностью вытеснительного поршня и верхней поверхностью рабочего поршня. Можно учесть и остальной объем под рабо­чим поршнем, называемый буферным, но это уже будет по­правкой к основным соотношениям. Рабочий и вытесннтельный поршни могут находиться или не находиться в физическом кон­такте; основные соотношения для этих двух случаев будут не­сколько отличными. Случай, когда рабочий и вытесннтельный поршни вступают в физический контакт, называют отрицатель­ным перекрытием.

А.2.1. Анализ случая отрицательного перекрытия

Рассмотрим систему, схема которой изображена на рис. А.2. Следует иметь в виду, что шток вытеснительного поршня про­ходит через полость сжатия. Можно полагать, что объем, за­нимаемый этим штоком, мал по сравнению с объемом полости

Рис. А.2. Двигатель модификации бета с отрицательным перекрытием.

Сжатия, хотя на самом деле это зависит от размеров двига­теля. Если размеры двигателя известны, объемом штока не сле­дует пренебрегать. Однако в начале конструктивных проработок размеры двигателя не заданы с достаточной точностью, и по­этому в анализе этот объем не будет учитываться.

А.2.2. Изменение объема полости расширения VE

VE = (1 + cos Ф)- (A. 160)

A.2.3. Изменение объема полости сжатия Vc

Vc = (1 - cos Ф) + [1 + cos (ф - a)] + Vno. (A.161)

Для удобства можно ввести отношение вытесняемых объемов kp, определяемое формулой

KP = VSP/VSE■ (АЛ 62)

Чтобы найти объем отрицательного перекрытия VKО, необходи­мо рассмотреть последовательность контактов рабочего и вы­теснительного поршней. Если поршни вступают в контакт, то в этот момент Vc = 0, и с помощью этого условия можно рас­считать Vjvo следующим образом:

Vc =^f- {(1 - cos Ф) + kp [1 + cos (Ф - «)]} + VNO = (A. 163)

— —jp-(l — cos Ф + kp + kp cos Ф cos a kp sin Ф sin a) + VN0 = V

F- 1(1 + kP) + (% ~ 2 kp cos a + l)"2 cos (Ф - p)] + VNo,

(A.164)

Kp sin a

Из соотношения (A.164) следует, что Vc достигает минимума при cos (ф — Р) = —1, и при отрицательном перекрытии этот минимум равен нулю. Следовательно,

О = ^ [(1 + kp) - {k2p - 2Kp cos a + l),/2] + VNO,

И в таком случае

VNO = ^f-[(k2p-2kpcosa+ 1)1/2-(1 +kp), (А. 166)

Vc = ^§Ч(1- cos Ф) + kp [1 + cos (Ф - a)] - (1 + kp) - f

-f- {kp — 2kp cos a + l)'/2} = (A. 167)

= [Kp cos (Ф-А)- cos Ф + (k2p - 2Kp cos a + l)1/2].

(A. 168)

A.2.4. Изменение давления

Изменение давления можно найти таким же образом, как И для двухпоршневого двигателя:

Мт = МЕ + Мс + MD = const = (А.6)

= (1 + <*»*) + (!- cos Ф) + К [1 + cos (ф-а)] -

- (1 + kp) + (k2p - 2Kp cos a + l)"2 + - i^-} . (A. 169)

Преобразуем тригонометрические члены

|(1 + cos Ф) + (1 - cos Ф) + kp [1 + cos(Ф -«)] = = | + £ cos Ф + 1 — cos Ф-- kp cos Ф cos А + kp sin Ф sin а =

= В + (1 + kp)] + [kl + 2 (g - 1) kp cos « + (g - L)2]"2 cos (Ф - 9),

(A. 170)

Kp sin a

Где 0 = arcsin —--------------------------------------------- Kttjj- . (A.171)

kp + 2(| — 1) fep cos а + — 1) J '

Следовательно,

(1 +M + [Ap + 2g - 1) kp cos a + (g 1)2]1/2X X cos - 8) - (1 + kp) + (k2P - 2Kp cos a + 1 )1/2 + y^-} =

+ g^T + + 2 (I - 1) kP cosa + (g - l)2]"2 cos tf - 0)}.

(A.172)

Применяя такие же рассуждения, как и при анализе двигателя компоновочной модификации альфа, получаем

Ј- = [g+(ft2_2ftpcosa+l)1'2 + 1fL] +

+ kl + 2 (g - 1) kp cos a + (g - l)2]"2 cos (Ф - 0) Пусть fl = [$ + 2(|-l)Јpcosa + (g - 1)2]'/2, (A.173)

5 = g + (^-2Apcosa+ O'^ + yfr, (A-174)

6 = B/S. (A.24)

В итоге получились соотношения такой же функциональной формы, как и для двигателя модификации альфа, и, следова­тельно, применимы такие же выражения для изменения давле­ния и переноса энергии, но с другими значениями fi, S, 6 и 0.

А.2.5. Параметр работы

Выражение для суммарного рабочего объема Vsr отлично от соответствующего выражения для двигателя модификации

Альфа по форме, но не по существу:

= VSB + (IГsb + YSP ~ VN0) = (А.49)

Г l + (fep ~• cos a + l)"2 "I = VSE [(2 + Kp)-- ^ + —-- ^ J = (A.175)

= [(3 + kp) + (k2P - 2Kp cos a + l)"2], (A.176)

VT=vST + vD =

= 1(3 + kp) + {k2P - 2Kp cos a + l)"2 + 2X], (A. 177)

VCt = ■(1 + cos Ф) + (1 - cos Ф) + [ 1+cos (Ф-А)]+

+ -%[0p-2Јpcosa + l)"2-(l +fep)] + A'FsЈ= (A. 178)

= +2X+(&2-2fcpcosa+ l),/2-f ftpcos(<Ј-a)].

(A. 179) (A.180)

1 + 2X + (ft2 _ Cos a + l)1'2 - Kp

И в итоге

26(1 — L) Я sin 6(1 —6)1/2 WtS= (I + б)"2 [l + (l - 62)"2] [3 + 2X + Kp + (ft2 - 2Kp cos a + l)"2] '

(A. 182)

A.2.6. Массовые расходы

Массовый расход в полости расширения определяется таким же выражением, как и для двухпоршневого двигателя, но вхо­дящие в него параметры определяются по-другому

• _ Vsepmax 0 -6)j {6 [sin (Ф - 6) - Sin 6] - Sin Ф) ш Ме 2i?7"c [1+6 cos (Ф — б)]2 '

Где параметры 0 и б определяются соотношениями (А.171), (А.173), (А. 174) и (А.24).

А.2.7. Массовый расход в полости сжатия Мс

Величина Мс определяется выражением Мс = PVdRTc, И, применяя соотношения (А. 168) и (А.31), получаем

Мс= 2 [1 /ЬТо^Ф - б)] RTC kP COS(*-a)-COS Ф +

+ (/# — 2/epcosa+l)1/2]. (А.183)

Пусть GB=P™* {l~^VsE, Dj = (kp — 2kpcosa + L)1'2;

D ( ) sin Ф — Kp sin (Ф — a) [Kp cos (Ф — a) — cos a + Ds] 6 sin (Ф — 6) "rftfT^ 1 + 6 cos (Ф — 6) ' [1 +6 cos (Ф — 6)]2 ~ =

= 6 [kp sin (a — 6) + sin 9 + D5 sin (Ф — 9)] + [kp sin (А—Ф)+ sin Ф]. Следовательно,

^ = ^ OP sin - 0) + sin 6 +

-f (k2p — 2Kp cos a + 1)1/2 sin (Ф — 8)] + (kp sin (А-Ф) + sin Ф)}.

(A. 184)

A.2.8. Анализ случая положительного перекрытия

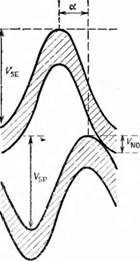
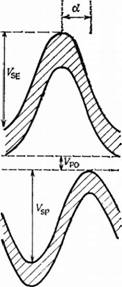
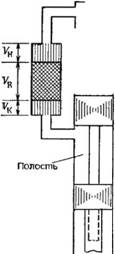
Изменения объемов в этом случае (рис. А. З) выражаются соотношениями

YB = -^L(l+cos Ф), (А. 160)

Vc = ■^f- (1 - cos Ф) + ^f- [ 1 + cos (Ф - A)] + Vp0- (A. 185)

Поскольку Vpo — постоянный объем в полости сжатия, можно предположить, что температура газа в нем равна температуре газа в холодной полости и что его можно включить в мертвый объем. Однако мы считаем, что если включить Vpo в мертвый объем, который практически равен объему теплообменников, то влияние перекрытия и влияние мертвого объема могут за­тушевываться. Поэтому мы предпочитаем рассматривать VPo как часть полости сжатия.

Рис. А. З. Двигатель модификации бета с положительным перекрытием. Изменения давления

Закон сохранения массы выражается соотношением МТ~МС + МЕ-- MD = const =

= Wf - (1 + Cos & + К [1 + Cos w - «)] +

+ (1-а»ф) + 2йЬ + - ррг}. (А-186)

Где ко = VPoIVSe = [(g + kp + 2k0+ +

-f cos фЦ + kp cos а — 1) -+ sin j> (kp sin a)] = = [0 + kp + 2k0 + + [k2p + 2 (| - 1) kp cos « +

+ (g-l)T2cos (ф — 6) j. (A. 187)

Параметры В, S, 0 и б можно определить по формулам

B = [k*p + 2(l - I) kp cosa + (£ — l)2]"2, (А. 188) 5 = § + kp + 2k, + АХШ + 1), (A. 189)

Б = B/S, sin Q = kp sin А/В. (A.24), (A.18)

В таком случае соотношения для переноса энергии будут такими же, как и для двигателя компоновочной модификации бета с отрицательным перекрытием или компоновочной моди­фикации альфа. Суммарный вытесняемый объем Vsr равен

VSr = FSE+Ksc= (А.48)

= VSE( 2 + kp). (A. 190)

Тогда VT = VsT + VD + VPO=VsE[(ko + kp) + (2 + X)], (A. 191)

X[l + cos (Ф — a)] + k{)VSE + = (A. l 92)

= [(2 + kp + 2k0 + 2X) + kp cos (Ф - a)]. (A. 193) Следовательно,

(^Сг)тах = (*0 + X) + (kp + 1), (A. 194)

(*0 + X) + (*p+l)

= (ko + x) + i • (A-195)

=-------- 1/2Г6(1Гё)^г('~б)1/2--------------- Г- (A-196)

RS (1 + 6)"2 [L + (L - б2)"2] [(£„ + *„) +(2+X)]

A.2.9. Массовые расходы

Массовый расход в полости расширения рассчитывается та­ким же образом, как и для других модификаций двигателя. Массовый расход в полости сжатия выражается соотношением

Mc = pVc/(RTc),

И, применяя формулы (А.31) и (А.185), получаем

МС = 2RT™[1+ 6cos (0S - 6)] t1 - C0S * + + k» C°S W ~ «) + ^ =

= 2^7+^(0-6)] [(1 +feP + 2feo) + fepcos(^-«)-cos^

(A.197)

Пусть GB Р - Гтах 6> Vse- . D6 = {1 + kP+ 2k,). Различие в

Соотношениях для двигателей модификации бета с отрицатель­ным и положительным перекрытием заключается в величинах двух постоянных Db и D6, так что в итоге получаем

Мс = здг^Г + I 1U6- 6)1* [fep sin (а - 6) + sin G +

+ (l + kp + 2k0) sin (Ф - G)] + kp sin (a - Ф) + sin (A. 198)