Реальный двигатель и псевдоцикл Стирлинга
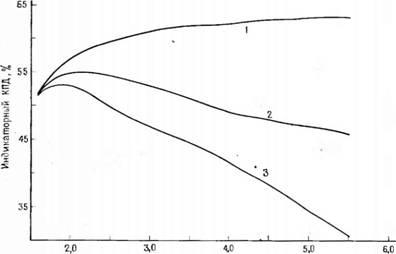
На основании данных, представленных на рис. 2.2, можно заключить, что при заданных значениях эффективности регенератора и разности температур термический КПД, относительный КПД и параметр полезной работы возрастают с увеличением степени сжатия. Следовательно, можно ожидать, что ре альные двигатели Стирлинга будут работать при степенях сжатия больше 5; однако если определить степень сжатия по
15 Зак. 839 опубликованным данным при использовании соотношений для идеального цикла, т. е.
RV = {T2p3WsPl), (2.14)
То получаются значения, заключенные между 2 и 3, и это подтверждается данными других исследований. Поэтому ясно, что модель идеального двигателя недостаточно точна. Однако Рал - лис и Уриелли [3] предложили модель псевдоцикла Стирлинга, в которой изотермические процессы заменены политропны - ми и в пределе адиабатными. Это довольно реалистическое
|
Ойъем |
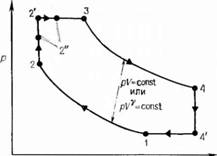
Рис. 2.3. Псевдоцикл Стирлинга.
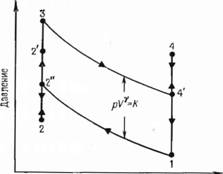
Предположение, поскольку вследствие «челночных» потерь при движении рабочего тела между двумя цилиндрами и конечных значений тепловых потоков идеальные изотермические условия не достигаются. Предлагаемая модель цикла показана на рис. 2.3. Идеальный изотермический процесс 1 — 2 заменяется адиабатным процессом 1 2" и изохорным процессом переохлаждения 2" — 2, а аналогичный процесс 3 — 4 заменяется процессами 3 - 4' и 4' — 4. Теперь полезная работа, производимая в цикле, Wx определяется соотношением
Wx=Wl2"+WM-Y Которое для адиабатного процесса принимает вид
Wx = MR [(Гз - 7V) - (7> - 7)]/(у - 1),
И, поскольку
Т =Т rv -1 и Т =Т У-1
1 2" 1 1 V 1 3 4 V »
Получаем
Wх = mRТ3 (1 - - (ry - 1)]/(V - 1). (2.15)
Применяя определение
Шъ = Г„
Приходим к выражению
Wx = MRT3 [(1 - Г~У) - I (rv 1 - I)]/(Y - 1). (2.16)
Теплоподвод Qs к системе в псевдоцикле Стирлинга равен
Qs = + Q-I-T'. И, поскольку величина Q34 = 0 (адиабатный процесс), Qs = MCv [(Г3 - Т, у) + (Г4 - ?V)]>
7У = 7з tE + (1 — ЕШ и 74=7,3. Следовательно, Qs = mtfJ,, [(1 - |) (1 - в) + (1 - 4-V)] (у - 1). (2.17)
В итоге КПД псевдоцикла г)пц можно найти, разделив соотношение (2.16) на (2.17):
Ч„ц=[0-^^-ЕК-'-ОИО-^+О-ЭО-»)J- (2Л8>
WO = Rv(L - гу-У) - I (/"Г1 - 1)]/[Б {Гу - 1) (Y - 1)]. (2.19)
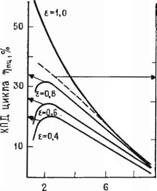
На рис. 2.1 представлены зависимость параметра полезной работы W0 от Rv при заданном отношении температур g и зависимости КГ1Д цикла г]пц от rv и е при том же самом отношении температур. Можно видеть, что максимальные значения до стигаются при rv ~ 2,5. В расчетах принималось, что рабочий газ по своим свойствам близок к воздуху, т. е. у = 1,4.
|
Степень сжатия rv Рис. 2.4. Параметры псевдоцикла в зависимости от степени сжатия. |
Анализ псевдоцикла Стирлинга показывает, что для заданных значений отношения температур и эффективности регенератора максимально возможный индикаторный термический КПД достигается при одной конкретной величине степени сжатия. При аналитическом исследовании этого явления [2, 3J было установлено, что, дифференцируя соотношение (2.18) по степени сжатия Rv, приравнивая полученное выражение нулю, чтобы найти максимум, и решая полученное квадратное уравнение относительно Rv, можно найти выражение для максимального КПД цикла, который не зависит от показателя
адиабаты газа и степени сжатия:
<U = «Ф - в) [(1 + в) - Е (1 + (1 + б)2], (2.20)
Где я]з = [1 — (1 +6)(l — eg-1)]0,5, (2.21а)
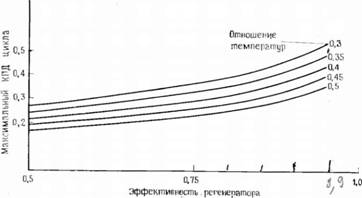
Соотношение (2.20) представлено графически на рис. 2.5.
Итак, зная отношение температур и эффективность регенератора, можно найти максимальный КПД проектируемого или созданного двигателя. В этом смысле очень полезно соотношение (2.20). Если применять исходное выражение для КПД
|
Рис. 2.5. Максимальный КПД цикла в зависимости от отношения температур и эффективности регенератора. |
(2.18), а также значения отношения температур и эффективности регенератора, как это делалось при расчетах, результаты которых приведены на рис. 2.5, то мы получим, что максимальная или оптимальная величина КПД достигается только при некоторой конкретной комбинации rv и у. Фактически можно найти универсальное значение оптимального фактора степени сжатия Г, при котором достигается максимальный КПД:
Г = 1. (2.22)
Это соотношение показывает, что достичь такого же КПД для воздуха, как, например, для гелия в одинаковых термодинамических условиях, т. е. при одинаковом изменении давления и температуры в цикле, можно лишь при более высокой степени сжатия, поскольку величина - у для гелия выше, чем для воздуха, и поэтому такое же значение Г будет получено при большей величине rv. Приведенное соотношение подтверждает также вывод одной из первых работ Михелса о том, что при заданных термодинамических условиях рабочие характеристики двигателя Стирлинга не зависят от параметров рабочего тела. Конструкция двигателя должна учитывать различные свойства рабочего тела, что отражается на размерах рабочего объема, теплообменника, расходе охладителя и т. п. Следовательно, двигатель, работающий на воздухе, будет тихоходнее и больше по размерам двигателя такой же мощности, работающего на водороде. Чем легче газ, тем меньше удельная мощность, рассчитанная как по массе рабочего тела, так и по массе двигателя.
Оказалось, что результаты, полученные при использовании псевдоцикла Стирлинга, соответствуют закономерностям и характеристикам реальных двигателей, хотя некоторые выводы и вызывают возражения. Основные сомнения связаны с интерпретацией идеального цикла, поскольку, по некоторым замечаниям. в нем используются газодинамические процессы, которые не достижимы или не встречаются в практическом двигателе. Подобные замечания справедливы, но довольно очевидны, поскольку идеальные циклы по определению состоят из идеальных и обратимых термодинамических процессов, которые не достижимы в реальных устройствах. Однако использование идеальных циклов и интерпретацию результатов последующего анализа необходимо согласовывать с практическими возможностями. Проблема заключается в том, как найти «золотую середину». Например, цикл с двойным сгоранием, используемый при анализе рабочего процесса, протекающего в дизеле, дает более «реальные» значения рабочих характеристик, чем исходный цикл дизеля, но его сочли гипотетическим циклом, выдуманным для того, чтобы получить приемлемые результаты, пока не отражающие идеальных характеристик дизельного двигателя [4J. Если бы критические замечания относительно псевдоцикла Стирлинга основывались на тех же доводах, они были бы более обоснованными. Во всяком случае, этот вопрос интересен в основном для педантов. Трудность проблемы состоит в том, что двигатели Стирлинга не работают по циклу Стирлинга, и в литературе царит путаница в вопросе о том, какие нужно применять критерии работы и рабочие характеристики.
При анализе тепловых энергосиловых установок, работающих по замкнутому циклу, применяются параметры разных категорий [4]: те, которые получены экспериментально, и те, которые получены в результате исследования идеальных термодинамических циклов для сравнимых условий. Первые можно назвать рабочими характеристиками, вторые — критериями работы. Сравнение данных, полученных этими двумя способами, позволяет судить о совершенстве конструкции и работы энергосиловой установки. Кроме того, правильная модель идеального цикла позволяет выявить закономерности процесса, зная которые можно усовершенствовать конструкцию двигателя; например, анализ цикла Отто показал, что увеличение степени сжатия приводит к возрастанию термического КГЩ двигателя и снижению удельного расхода топлива, что и было подтверждено на практике. Однако следует всегда помнить о том, что критерии работы получены не на практической основе, а путем теоретического исследования обратимых термодинамических циклов. Следовательно, модели идеальных циклов не следует смешивать с моделями двигателей или с моделями рабочих процессов, в которых достаточно точно воспроизводятся потоки энергии и расходы рабочего тела, действительно имеющие место в реальных двигателях. Для большинства тепловых энергосиловых установок с замкнутым циклом работы действительно существуют адекватные модели идеального цикла, но до сих пор не найдено полностью удовлетворительного идеального цикла двигателя Стирлинга, что можно считать иронией судьбы, поскольку он является одной из немногих энергетических установок, действительно работающих по замкнутому циклу.
Существует несколько модификаций двигателя Стирлинга, но, видимо, слишком оптимистично было бы предполагать, что один и тот же идеальный цикл применим ко всем типам двигателя Стирлинга. Поскольку идеальные циклы касаются только термодинамики энергосиловой установки, отличие конкретного рабочего параметра от эквивалентного ему критерия работы служит мерой отклонения механических и гидравлических характеристик сконструированной системы, обусловленного выбранным механизмом привода, материалом и конструкцией теплообменника, конструкцией уплотнений, относительным мертвым объемом и т. д. При анализе идеального цикла возникают две основные проблемы: во-первых, используемый цикл должен правильно описывать термодинамические особенности рабочего процесса (например, нельзя описывать адиабатный процесс как изотермический и наоборот); во-вторых, нужно выбирать наиболее полезные для практики, т. е. измеряемые, критерии работы, в противном случае анализ будет представлять лишь академический интерес. При анализе двигателя, работающего по циклу Стирлинга, наиболее трудной является, по-видимому, первая проблема. Если предположить, что процесс обмена энергией происходит в рабочих полостях переменного объема, то принципиально правильными в предельном случае будут модели изотермического процесса. Однако если в систему входят отдельные теплообменники, то перенос энергии в рабочих полостях переменного объема обычно мал по сравнению с переносом энергии в указанных теплообменниках, и в этом случае более точным будет предположение о том, что процесс газообмена в рабочих полостях является адиабатным или изоэн- тропным в идеальном смысле.
Действительно, как было показано выше, применение изо- энтропного процесса в псевдоцикле Стирлинга позволяет правильно выявить закономерности, наблюдаемые на практике, и, как отмечалось в работе [2], полученные значения индикаторного термического КПД хорошо согласуются с измеренными значениями. Однако результаты более подробного анализа рабочего процесса, в котором помимо основных термодинамических характеристик рассматривались факторы теплообмена и
|
V Рис. 2.6. Диаграмма состояния цикла, состоящего из шести процессов. |
Газовой динамики, показали, что явление правильно описывает изотермическая модель [5]. Кроме того, результаты исследования двигателей компоновочной модификации поршень — вытеснитель [6, 7] показали, что циклы, состоящие из четырех процесов, неадекватны и должны быть заменены циклами, состоящими из шести процессов, так как в рабочем цикле теплообмен с внешней средой и с регенератором происходит не исключительно в изохорных условиях, а как в изохорных, так и в изобарных условиях. Действительно, согласно экспериментальным данным Треска [6], большая часть циклического процесса поглощения тепла происходит в изобарных условиях. Предполагалось, что процессы обмена в рабочих полостях протекают изотермически, и Раллис [8] обобщил концепцию цикла, состоящего из шести процессов, с учетом предположения об изоэнтропности рабочего процесса. Этот цикл показан на рис. 2.6.
В свете изложенного ясно, что исследования идеального цикла привели к несколько противоречивым результатам, особенно если учесть, что изотермические и изоэнтропные модели являются всего лишь предельными случаями более общей по - литропной модели. Таким образом, при выборе модели рабочего процесса возникает определенная дилемма, которая влияет не только на анализ идеального цикла, но и на более сложное численное моделирование процесса на ЭВМ. Чтобы решить этот вопрос, было проведено строгое аналитическое исследование различных идеальных циклов с точки зрения требуемых критериев работы [9, 10].
Для отыскания критерия, с которым можно было бы сравнивать измеряемый параметр, требуется провести подробное исследование идеальных циклов, осуществляющихся при термодинамических условиях, сравнимых с условиями, характерными для реальных энергетических установок. На выбор и функциональную форму критериев в большой степени влияют те параметры или группа параметров исследуемой системы, которые поддаются измерениям. В предыдущих исследованиях двигателей Стирлинга рассматривались два критерия — КПД двигателя и безразмерный параметр полезной работы. Для псевдоцикла эти параметры определяются соотношениями (2.18) и (2.19). В своих исследованиях различных циклов Кросс и Ридер ввели еше один критерий — так называемое отношение работ, который используется обычно применительно к турбинам.
Поскольку влияние необратимости неодинаково для различных тепловых двигателей или классов этих двигателей, действительные термические КПД реальных энергетических установок могут существенно отличаться друг от друга, даже если значения идеальных КПД соответствующих идеальных циклов одинаковы. Поэтому высокий КПД идеального цикла не всегда соответствует высокой эффективности энергетической установки. Необходимо оценить степень необратимости рабочего процесса в установке и определить влияние этой необратимости на характеристики установки, чтобы правильно представить особенности системы. Такой мерой влияния необратимости является критерий, называемый отношением работ для никла:
™ ___ Реальная индикаторная полезная работа ^ 23V
R Индикаторная полезная работа ' 1 '
Поскольку необратимость вызывает уменьшение полезной работы и увеличение потерь работы, низкое идеальное значение WR означает, что из-за небольших отклонений в конструкции полезная работа энергосиловой установки может стать равной нулю. И, наоборот, система с большим идеальным значением WR не должна быть слишком чувствительной к подобным отклонениям, и в этом случае можно ожидать высокого значения реального КГЩ всей системы. Кроме того, было бы полезно иметь критерий, определяющий сравнительные размеры или тип установки для заданной полезной мощности. В этом случае также можно использовать критерий отношения работ, но, когда это отношение стремится к максимальному значению, равному 1, оно несет меньше информации о размерах установки, однако параметр работы Раллиса W0 восполняет недостающую информацию.
Итак, можно сделать вывод, что если система имеет высокий КПД идеального цикла и одновременно высокое отношение работ, то можно ожидать высокого суммарного КПД реальной установки. Рассматривая дополнительно параметр работы V0, Можно выбрать тип и до некоторой степени оценить размеры установки. С помощью выбранных критериев был проведен анализ различных циклов, состоящих из четырех и шести процессов. Рассматривались семь циклов: четыре -— из четырех процессов и три — из шести. Сводка циклов дана в табл. 2.1.
Таблица 2.1. Возможные модели идеального цикла двигателя Стирлинга
Название цикла
Идеальный цикл Стирлинга (RS) Регенеративный цикл
Отто IRO) Псевдоцикл Стирлинга (PS)
Цикл Треска (Т) Цикл Раллнса (R)
Процесс расширения/ процесс сжатия
Изотермический
Изоэнтропный
»
Изотермический Изоэнтропный
Число процессов
4 4
4 (с двумя дополнительными изохорными процессами переноса энергии)
6 6
Дополнительно рассматривались «политропные» варианты модельных циклов, состоящих из четырех и шести процессов. Большинство соотношений для идеального двигателя Стирлинга и псевдоцикла Стирлинга уже было выведено, и их применимость обсуждалась ранее. Формулы, выражающие критерии для различных модельных циклов, выводились на основании обших определений этих критериев, заданных соотношениями (2.4), (2.12) и (2.23). Для более сложных моделей требуется провести более трудоемкие и сложные математические действия с основными соотношениями, чтобы получить нужные формулы, и с целью экономии места мы не даем промежуточных выкладок, а приводим только итоговые соотношения. Однако вывод различных выражений можно найти в работах [2,
8—113-
Термический КПД
При выводе соотношений для термического КГ1Д модельных циклов всегда применялось одно и то же определение эффективности регенератора е, основанное на отношении температур.
Регенеративный цикл Отто (RO)
Чяо^О-'-И-Ц^-ОИО-Ч (2-24)
Цикл Треска — Стирлинга (TS)
Поскольку этот цикл состоит из шести процессов, перенос энергии происходит как в изохорных, так и в изобарных условиях, и в итоге получаются два соотношения для термического КПД: одно — для случая полной регенерации в изохорной фазе (TS1), а другое — для случая регенерации в изобарной фазе (TS2):
(У - 1) [Я„(1 + In rVE) + %н (1 - Ш Rvc) - (i + Itsi *ff[(Y-e)-E(l-e)] + (Y-l)(^lnr„Ј-l) '
_ (v-l)(^„lnryE-l) + ;.„[(y-e)-6(1-e)l ^Tsa 'ITS. ^[Y(l-e)(l-g) + (Y-l)lnrVE] '
Поскольку в циклах, состоящих из шести процессов, можно иметь различные степени сжатия в двух рабочих полостях переменного объема, член rv обозначается соответственно через rVE и Гус - Кроме того, для удобства расчетов вводятся отношения температур при изохорном нагреве и изобарном охлаждении, чтобы упростить приведенные выше выражения. Первое отношение обозначается через %н, второе — через обращаясь к рис. 2.6, получаем
= TJTU (2.27)
КK = Ti-/Tl. (2.28)
Цикл Раллиса (R)
|
(2.29) |
Этот цикл также состоит из шести процессов, и, следовательно, также получаются два соотношения для КПД:
У (1 + £) - (V - 1) (Мя ~ 0 ~ № + Е4ё')
1ri yO-^ + ^-i-K^ + ^c1) '
•n - г, + + , 3m
Отношение работ
Для всех рассматриваемых идеальных циклов отношение работ выражается универсальной формулой
WR = -Zl. (2.31)
Очевидно, желательно иметь нулевое значение Z, поскольку, чем больше величина Z, тем сильнее характеристики цикла зависят от необратимости рабочего процесса. В табл. 2.2 приведены расчетные формулы для параметра Z в различных циклах.
Таблица 2.2. Расчетные формулы для параметра необратимости Z
Цикл Формула
RS 1 (2.32а)
RO гу] (2.326)
|
(2.32д) |
PS (2.32в) Rv^n-rvc(-lnrvc) Гус [(1 + In rKЈ)-V]
RVE (1 - Y) rvc + XHryvy (у - rfe1) (l-Y) + XHrW (y-^EV)
Параметр полезной работы
С помощью определения (2.23) были найдены соотношения для параметра полезной работы, которые, как можно видеть, несколько сложнее соответствующих выражений для отношения работ:
Г., (1 — |)
RoRs= 6(г ц 'п Гу, (2.33)
^ORO = I(v-I?(ry-1) К1 - rv y) - 6 (Т' - 1) J. (2-34)
L^oTS = .. LVE ■ [(1 + In rVE) + 1(1 - In Гус) - (W +
|
^oR |
(2.35)
= E(v-0(ryc-i) [(V - + I (V - Тс') +
Понятно, что, используя приведенные выражения для рассматриваемых критериев, можно получить большое количество данных для определения оптимальных значений степени сжатия, отношения температур и т. п. (что и было сделано в работах [2, Ю]), но наша цель состоит в том, чтобы сравнить различные модели циклов с помощью трех указанных критериев.
И найти основные закономерности. Поэтому мы не рассматриваем влияния изменения отношения температур и эффективности регенератора на выбранные критерии работы для всех циклов и приводим результаты расчетов при постоянных значениях отношения температур 0,33 и эффективности регенератора 0,85 для водорода и гелия, выбранных в качестве рабочих тел. Для всех идеальных циклов основные параметры определены одинаково, и, кроме того, для циклов, состоящих из шести процессов, заданы относительный нагрев Хи и относительное охлаждение Прежде всего рассчитаны критерии работы. На рис. 2.7 представлены результаты расчета термического КПД для циклов, состоящих из четырех процессов.
|
58
|
|
|
|
Рис. 2.7. Сравнение результатов расчета термического КПД для циклов, состоящих из четырех процессов. 1 — идеальный цикл Стирлинга; 2 — регенеративный цикл Отю; 3 — псевдоцикл Сгнр линга. |
|
34 |
Сравнение регенеративных циклов Стирлинга и Отто позволяет, по существу, выявить влияние различных условий (адиабатных или изотермических) протекания процесса сжатия и расширения рабочего тела. Расчетные значения КПД этих
двух циклов практически не различаются при степени сжатия до 1,8 и слабо различаются при степени сжатия гv до 2.2. Однако при более высоких значениях rv расхождение становится все значительнее, так что при степенях сжатия более 3,0 величины КГ1Д могут различаться на 10 % и более. Хотя характер изменения КПД для регенеративного цикла Отто и псевдоцикла Стирлинга примерно одинаков, по абсолютной величине КПД существенно различаются. Несмотря на сходство в том, что оба цикла имеют оптимальную степень сжатия, составляющую в рассматриваемых условиях 2,1 для псевдоцикла Стирлинга и 2,3 для цикла Отто, абсолютные значения КГ1Д систематически различаются примерно на 8 %• Это различие
|
2 Степень сжатия |
|
А |
Рис. 2.8 Сравнение результатов расчета термического КПД для циклов, состоящих из шести процессов. I—цикл Треска; 2—цикл Раллиса.
Обусловлено «хвостами» псевдоцикла (процессы 2 — 2' и 4 — 4' на рис. 2.3), учитывающими теплообмен рабочих полостей переменного объема с внешней средой. Для циклов, состоящих из шести процессов (рис. 2.8), наблюдается аналогичный характер изменения термического КГЩ: изотермический цикл Треска обладает более высоким КПД, чем адиабатный цикл Раллиса. Лишь при очень низких степенях сжатия КПД обоих циклов одинаковы. Однако важно отметить, что при определенных условиях циклы из шести процессов могут иметь более высокий КПД, чем циклы из четырех процессов. Для всех рассмотренных циклов и адиабатные, и изотермические модели являются предельными случаями модели рабочего процесса, который в действительности является политропным. О влиянии политропности процесса можно судить по представленным на рис. 2.9 данным, которые показывают, что изотермический случай служит верхней, а адиабатный -— нижней границами действительных значений. Однако отметим, что данные для поли - тропного и адиабатного циклов имеют одинаковый характер изменения, и поэтому адиабатные циклы, по-видимому, точнее моделируют реальные процессы. И в этом случае расчетные значения КПД для различных циклов очень мало отличаются при низких степенях сжатия.
Результаты расчета критерия отношения работ (рис. 2.10 и 2.11) показывают, что при возрастании степени сжатия " адиабатные циклы сильнее зависят от степени необратимости рабочего процесса, поскольку величина Wr понижается.
|
Степень сжатия Рис. 2.9. Сравнение результатов расчета КПД для изотермической, адиабатной и политропной моделей цикла. 1—цикл Треска; 2— политропный цикл; 3 — цикл Раллиса. |
|
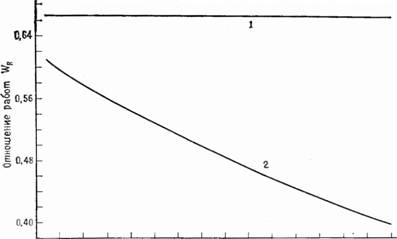
2,0 2,8 3,6 4,4 Степень сжатия Рис. 2.10. Изменение отношения работ для циклов, состоящих из четырех процессов. I—изотермический цикл из четырех процессов; 2 — адиабатный цикл из четырех процессов. |
Что касается изотермических моделей, то для цикла из четырех процессов отношение работ не зависит от степени сжатия а для цикла Треска отношение работ монотонно возрастает с увеличением степени сжатия. Аналогичным образом изменяется третий из рассмотренных критериев — параметр полезной работы, и поэтому мы не приводим соответствующих расчетных данных, которые можно найти в работе [10].
|
Степень сжатия |
Если эти циклы рассматривать как некие эталоны, по которым можно судить о характеристиках реальных двигателей, работающих по циклу Стирлинга, то следовало бы как-то обосновать это утверждение. В качестве примера используем значения параметров двигателя 4-235 фирмы «Филипс» и рассчитаем идеальный индикаторный термический КПД двигателя, пред-
Рис. 2.11. Изменение отношения работ для циклов, состоящих из шести процессов. 1 — цикл Треска; 2 — цикл Раллиса.
Полагая, что он работает по одному из рассмотренных циклов. Метод, с помощью которого проводятся расчеты такого типа, описан в работе [2].
Хотя опубликованы результаты измерения не индикаторного, а эффективного КПД, обе эти величины можно связать соотношением
■Цв =
Где индексы В, I и М относятся соответственно к эффективному, индикаторному и механическому КПД. Используя расчетные значения гр, полученные на основании предыдущего анализа идеальных циклов, и опубликованные величины 1]в, можно рассчитать значения механического КПД. Хотя до сих пор в открытой печати не публиковались данные о механическом КПД двигателей, можно полагать, что он составляет около 80 %. Расчетные значения механического КПД будут выше, если анализ идеального цикла дает заниженное по сравнению с истинным значение термического КПД, и ниже этой величины — в противоположном случае. Анализ цикла или циклов, в которых использовались правильные критерии работы, должен приводить к значениям приблизительно 80 %. В таком случае независимо от того, какая из идеальных моделей рабочего процесса — адиабатная или изотермическая — использована в этих циклах, она является достаточно точным приближением
реальных процессов. Полученные таким образом результаты представлены в табл. 2.3.
|
Таблица 2.3. Значения КПД, рассчитанные по результатам испытаний двигателя 4-235 фирмы «Филипс»
|
На основании данных, приведенных в этой таблице, можно было бы сделать вывод о предпочтительности псевдоцикла Стирлинга, но следует иметь в виду, что при проведении расчетов не учитывалось влияние мертвого объема и отклонений в конструкции вспомогательных устройств двигателя 4-235 и, кроме того, вероятно, величина расчетного механического КПД, составляющая 78 %, является завышенной. Этот вопрос можно разрешить лишь с помощью более подробных результатов испытаний двигателей, которые пока, к сожалению, отсутствуют. Тем не менее можно видеть, что наиболее подходящими являются циклы, в которых процессы считаются адиабатными, и, видимо, этот путь обеспечивает достаточно точное моделирование рабочего процесса. Однако было показано, что при низких степенях сжатия влияние адиабатного процесса не настолько важно, как это первоначально предполагалось.
Мы уже отмечали, что наиболее перспективным циклом (или циклами) является тот, который имеет одновременно и высокий КПД, и высокое отношение работ. Для всех рассмотренных циклов это достигается при низких степенях сжатия, что следует иметь в виду при проектировании регенеративных тепловых двигателей. Некоторые из этих циклов недостаточно эффективны с точки зрения критериев работы для двигателя Стирлинга в том смысле, что расчетные закономерности отличаются от экспериментально измеренных, но тем не менее эти закономерности свидетельствуют, что, используя эти циклы, можно создать высокоэффективные энергосиловые установки, и это стимулирует, учитывая современные энергетические проблемы, продолжение исследований.
Согласно результатам анализа псевдоцикла Стирлинга, включение в цикл процессов, учитывающих теплообмен с внешней средой, оказывает более сильное влияние, чем использование различных моделей рабочего процесса. Поэтому простая замена изотермического процесса адиабатным (особенно при низких степенях сжатия) не дает большого эффекта. Значительно эффективнее использование адиабатного процесса с последующим процессом теплообмена.
Идеальные циклы могут быть полезны в качестве приближенных моделей реальных циклов, и, кроме того, в некоторых случаях они могут стать основой для более точных аналитических моделей. Однако их не следует смешивать с моделями, которые используются при анализе или моделировании рабочего процесса с целью оптимизации конструкции реального двигателя. В более точных аналитических моделях используются как изотермические, так и адиабатные процессы, причем предпочтение отдается последним. Исследования идеальных циклов типа проведенного нами позволяют дать более строгое научное обоснование этим предположениям о характере рабочего процесса и оправдать их использование. Хотя результаты нашего анализа и не позволяют сделать окончательных выводов вследствие недостаточности экспериментальных данных, они убедительно показывают, что газовые процессы в рабочих полостях переменного объема можно считать адиабатными, но можно без большой ошибки применить предположение об изотермич - ности процессов, если не учитываются процессы теплообмена с внешними теплообменниками. Результаты анализа показали также, что из всех рассмотренных циклов наиболее подходящим является, видимо, псевдоцикл Стирлинга, но только для работающих по циклу Стирлинга двигателей модификации альфа, предложенной Раллисом.
Итак, мы рассмотрели идеальные термодинамические характеристики двигателя Стирлинга, и, хотя исследовалось влияние реального двигателя на параметры выбранного идеального цикла, т. е. влияние адиабатного процесса по сравнению с изотермическим, и влияние внутренних теплообменников по сравнению с теплоотводом в стенки цилиндра, практические особенности общей системы не учитывались. Теперь для наглядности мы рассмотрим по отдельности влияние различных практических факторов, вызывающее отклонение цикла реального двигателя от идеального цикла. Влияние практических факторов будет показано на примере цикла, состоящего из четырех процессов.