Железобетон

Расчет поперечных стержней

Ем без отгибов, что часто встречается в практике.

Расчетным из всех воз­можных наклонных сече­ний, начинающихся в точ­ке В (рис. 111.20), явля­ется сечение, которое име­ет наименьшую несущую способность. Учтем на ос­новании рис. 111.20 и фор­мул (III.59) и (111.60), что Qd = Q — Рс

Asw Qsw О

Где Q—поперечная сила в на­чале наклонного сечения (рис. 111.20); QsШ — усилие, воспри­нимаемое поперечными стерж­нями, отнесенное к единице длины элемента.

Из выражения (III.62), принимая во внимание, что коэффициенты = 0, флг=0, находим

Д6=ФмЛм«2/с = В/с, (III.81)

Рассмотрим изгибаемый элемент прямоугольного по­перечного сечения, без предварительного напряжения, с поперечным армировани-

Где

(II 1.82)

В-.

<Fb2RBt Bh0-

Подставив выражения (111.81) и (III.80) в формулу (111.58), с учетом равенства (111.60) найдем

Q<(Qsa>+P)C+ В/с, (III. 83)

11*

163

Наименьшая несущая способность наклонного сече­ния, очевидно, определится из условия

DQ/Dc = (Qsw + р) — В/с? = 0.

Отсюда получаем значение проекции расчетного на­клонного сечения

С = V B/(Qsw + P) = У фй Rbt Bh20/(Qsw + р) . (Ill. 84)

Подставив это значение в выражение (111.83), полу­чим условие прочности по поперечной силе с учетом на­именьшего значения несущей способности наклонного се­чения:

Q< 2/ B(Qsw + P) .

С учетом значения В по формуле (111.81) поперечная сила Qwb, воспринимаемая хомутами и бетоном в расчет­ном наклонном сечении,

= 2/фюЯм^о (?«, + *) • ("1.85)

В реальных условиях во многих случаях нагрузка р принимается равномерно распределенной только для рас­чета, а на самом деле она сосредоточена в отдельных местах. Может оказаться, что на протяжении наклонного сечения она в действительности отсутствует. Поэтому на­грузку следует учитывать лишь тогда, когда она факти­чески равномерно распределена, как, например, при да­влении воды или грунта.

Принимая Р=0 в формулах (111.84) и (111.85), нахо­дим, что несущая способность сечения по поперечной си­ле, обеспечиваемая сопротивлением бетона сжатой зо­ны и сопротивлением хомутов, равна:

= <9ь2*ьМЯвш. (III.86)

При этом длина проекции расчетного наклонного се­чения определяется выражением

Co=V<tb2Rbtbhl/4aW. (111,87)

На основании схемы, изображенной на рис. 111.20, можно записать соотношение

QSwS — RswAswn, (III. 88)

Где s —шаг поперечных стержней (хомутов); Aaw — сечение одного поперечного стержня (одной ветви хомута); п — число поперечных стержней в сечении элемента.

В расчетах обычно задаются диаметром поперечных стержней и их числом в поперечном сечении элемента, оперируя далее значением Aswn как известным.

Из выражения (III.86) определяют требуемую интен­сивность поперечного армирования, имея в виду, что заданное Q = Qwb — Qw^-Qb, -

Я^&ЪъЫЬНы- (ш-89>

Этому значению Qsw Должно отвечать усилие в хомутах на одиницу дли­ны элемента

Q$w = RSwASwN/s. (ill.90)

Пользуясь этой фор­мулой, нужно иметь в ви­ду, что вводимая в расчет по формуле (111.89) попе­речная сила Q, как следу­ет из анализа выражений (ПІ.83) и (111.84), воспри­нимается поровну попе­речной арматурой и бето­ном, т. е.

Qb — Qao — 0,5Q.

Согласно требованию (III.63), это значение Q& должно быть не менее

QbXPuRbtbh,. (III.91)

При установлении шага поперечных стержней поми­мо расчетных условий должны приниматься во внимание также конструктивные требования (см. § III. 1).

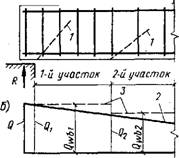
На отдельных участках балки интенсивность попе­речного армирования (шаг, диаметр стержней) может быть различной. Начало расчетных наклонных сечений выбирают на грани опоры, где Qi = Qwbu и в. месте, где Q=Qwb2 (рис. III.21,а). Соответственно принимаются расчетные значения поперечной силы. Участок 1 элемен­та с интенсивностью Qsw простирается от опоры до ме­ста, где Q = Qwb2 (рис. III.21,a), за которым начинается участок 2 с интенсивностью поперечного армирования

О)

Si Si Sf Sf 5/ Sp So

I f r t t r

Рис. 111.21. Расчетные наклонные сечения на участках балки с раз­ным шагом поперечных стержней

А — расчетная схема; б— эпюры поперечных сил; I — расчетные наклонные сечения; 2 — эпюра Q из статического расчета балки; 3 — очертание эпюры Qmb