Приведенное сечение
Чтобы определить напряжения в сечениях предварительно напряженных железобетонных элементов в стадии I до образования трещин, рассматривают приведенное бетонное сечение, в котором площадь сечення арматуры заменяют эквивалентной площадью сечення бетона. Исходя нз равенства деформаций арматуры н бетона, приведение выполняют по отношению модулей упругости двух материалов V=Es/Eb. Площадь приведенного сечення элемента составит (рнс. II.7, б)
ARed = A + VASp + VAS + VASp + VAS> <"-28)
Где А — площадь сечения бетона за вычетом площади сечения каналов и пазов.
Статический момент приведенного сечення относительно осн /—/, проходящей по нижней грани сечення:
Sred — 2At У І, (11.29)
Где At — площадь части сечения; yi— расстояние от центра тяжести І-Й части сечения до оси I—/.
Расстояние от центра тяжести приведенного сечення до осн 1-І
Y0 = Sred/Ared■ ("-30)
Момент инерции приведенного сечення относительно оси, проходящей через центр тяжести приведенного сечення:
/гЄ£г = 2[/г + Лг(у0-«/г)2]. (11.31)
Где U — момент инерции І-Й части сечення относительно оси, проходящей через центр тяжести этой части сечения.
Расстояние до верхней н нижней границы ядра сечения от центра тяжести приведенного сечення составят:
Г= Ітей/Ared Уо' RTn1 = Lredl[Ared (Л —J/0)l - (11.32)
Напряжения в бетоне при обжатии
При обжатнн в бетоне развиваются неупругне деформации, эпюра нормальных напряжений приобретает криволинейное очертание. В упрощенной постановке напряжения в бетоне при обжатнн определяют в предположении упругой работы сечення и линейной эпюры напряжений
ОЬР = PIAred ± Ре0р Ytlred• (11-33)
В зависимости от дели расчета напряжения в бетоне определяют в разных по высоте сечения уровнях:
А) при установлении контролируемого напряжения в арматуре, натягиваемой на бетон, напряжения в бетоне определяют в уровне усилий в напрягаемой арматуре:
СТьр = P/Ared + Ре0р У$р/IreS (11.34)
°ЪР = P/ARed - Р% У Spared' (" • 35)
Где Р определяют с учетом первых потерь при у«Р=1.
Б) при проверке предельных напряжений при обжатии напряжения в бетоне определяют в уровне крайнего сжатого волокна
0Ьр = PIAred + Ре ОР У о/1 Red- (11.36)
Здесь Р определяют с учетом первых потерь (без потерь ов) при Y»p=l.
В) при расчете потерь о6 от быстронатекающей ползучести и <т9 от ползучести напряжения в бетоне определяют на уровне центра тяжести напрягаемой арматуры по формулам (11.34) и (11.35).
7. Последовательность изменения предварительных напряжений в элементах после загружения внешней нагрузкой
Центрально-растянутые элементы. При изготовлении элемента арматуру натягивают до начального контролируемого напряжения Осоп на упоры форм, производят бетонирование, тепловую обработку и выдерживают в форме до приобретения бетоном необходимой передаточной прочности Rbp. В этом состоянии 1 произошли первые потери oiosi в основной их части (рис. II.8). Затем при освобождении с упоров форм и отпуске натяжения арматуры благодаря сцеплению материалов создается обжатие бетона, развиваются деформации быстронатекающей ползучести и происходят потери ов— состояние 2. Предварительное напряжение в арматуре с учетом упругого обжатия бетона равно осоп—От—v<r&p, здесь aiosi— без потерь <Тз, <Т4, поскольку последние учитываются в (Тсоп-
С течением времени происходят вторые потери Olos2, Соответственно уменьшаются и упругие напряжения в бетоне — состояние 3. Предварительное напряжение в арматуре с учетом полных потерь и упругого обжатия бетона в этом состоянии равно оС0П—ош—хоьрі.
После загружения элемента при постепенном увеличении внешней нагрузки напряжения в бетоне от предварительного обжатия погашаются — состояние 4. Предварительное напряжение в арматуре с учетом потерь на уровне нулевого напряжения в бетоне в этом состоянии равно: Os-P = Ocon—Oi0S-
Дальнейшее увеличение нагрузки приводит к появлению в бетоне предельных растягивающих напряжений Rbtn — состояние 5, т. е. конец стадии I напряженно-деформированного состояния.
Приращение напряжений в растянутой арматуре после погашения обжатия в бетоне исходя из предельной растяжимости бетона Eubt=-2Rbtn/Eb и совместности деформаций двух материалов
As = 8S Es = Eubt Es = (2Rbtn/Eb) Es = 2VRbtn.
6m~6to$i Бсап'^іоі
-f -
Состояние 2
ВыгиГ4- ж -6Losi. Щ Соствяние 3
Напряжение в напрягаемой растянутой арматуре перед образованием трещин равно Asp + 2VRbtn■ Оно превышает соответствующее на- Состояние I Пряжение в элементах без — предварительного напряже - , Ния на Gap, что повышает со-
Противление образованию трещин. После образования трещин в стадии II напряженно-деформированного состояния растягивающее усилие воспринимается арматурой. По мере увеличения нагрузки трещины раскрываются. При дальнейшем увеличении нагрузки напряжения в арматуре становятся предельными н происходит разрушение — стадия III.
, При натяжении арматуры на бетон последовательность напряженных состояний аналогичная. Отличие в период изготовления и до загружения элемента внешней нагрузкой заключается в том, что начальное контролируемое напряжение арматуры определяют с учетом обжатия бетона.
Изгибаемые элементы. При натяжении на упоры форм верхнюю и нижнюю арматуру натягивают на величину начальных контролируемых напряжений <тс<т, оСоп (рис. II.9). Обычно принимают оСоп = оСоп - После бетонирования и твердения в процессе тепловой обработки происходит основная часть первых потерь предварительных напряжений в арматуре — состояние 1. После приобретения бетоном необходимой прочности арматура освобождается с упоров форм и обжимает бетон; предварительные напряжения в арматуре в результате быстронатекающей ползучести н упругого обжатия бетона уменьшаются — состояние 2. При этом вследствие несимметричного армирования Л5р >А sр и внецентренного обжатия элемент получает выгиб. С течением времени происходят вторые потерн напряжений арматуры aiosi—состояние 3. После загружения внешней нагрузкой погашаются напряжения обжатия в бетоне — состояние 4. Предварительное напряжение в арматуре на уровне нулевого напряжения в бетоне в зоне, растянутой от действия внешней нагрузки, в этом состоянии
<*Sp — Ocon — Olos- (11.37)
При увеличении нагрузки напряжения в бетоне растянутой зоны достигают предельных Rbtn — состояние 5. Это и будет концом стадии I напряженно-деформированного состояния при изгибе. В этой стадии напряжение в арматуре равно ASp + 2VRbtn■ При изгибе, как и прн растяжении, перед образованием трещин напряжение в растянутой арматуре превышает соответствующее напряжение в арматуре элементов без предварительного напряжения на Osp. Этим и определяется значительно более высокое сопротивление образованию трещин при изгибе предварительно напряженных элементов. При увеличении-нагрузки в растянутой зоне появляются трещины, наступает стадия II напряженно-деформированного состояния. С дальнейшим увеличением нагрузки растягивающие напряжения в арматуре и бетоне достигают предельных, происходит разрушение — стадия III. Напрягаемая арматура площадью сечения Asp, расположенная в зоне, сжатой от действия внешней нагрузки, деформируется совместно с бетоном сжатой зоны, при этом предварительные растягивающие напряжения в ней уменьшаются. При предельных сжимающих напряжениях в бетоне напряжения в напрягаемой арматуре этой зоны
A =R —а'. (11.38)
SC sc SP 1 '
Напряжение asp определяют с коэффициентом точности натяжения ysp>l и с учетом потерь. При Asp<Rsc Арматура площадью Asp сжата, а при ASp>RSc растянута и в этом случае несколько снижается несущая способность предварительно напряженного элемента.
§ II.5. ГРАНИЧНАЯ ВЫСОТА СЖАТОЙ ЗОНЫ. ПРЕДЕЛЬНЫЕ ПРОЦЕНТЫ АРМИРОВАНИЯ
1. Граничная высота сжа»той зоны -
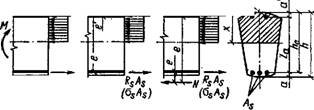
В сечениях, нормальных к продольной оси элементов,— изгибаемых, внецентренно сжатых, внецентренно растянутых—при двузначной эпюре напряжений в стадии III характерно одно и то же напряженно-деформированное состояние (рис. 11.10). В расчетах прочности усилия, воспринимаемые сечением, нормальным к продольной оси элемента, определяют по расчетным сопротивлениям материалов с учетом коэффициентов условий работы. При этом принимают следующие исходные положения: бетон растянутой зоны не работает — сопротивление Rbt равно нулю; бетон сжатой зоны испытывает расчетное сопротивление Rb — эпюра напряжений прямоугольная; продольная растянутая арматура испытывает напряжения, не превышающие расчетное сопротивление Os^Rs', продольная арматура в сжатой зоне сечения испытывает напряжение Osc. В общем случае условие прочности при любом из перечисленных внешних воздействий формулируется в виде требования о том, чтобы момент внешних сил не превосходил момента внутренних усилий. Запишем это условие относительно оси, проходящей через центр тяжести растянутой арматуры:-
+ (11.39)
Где М — в изгибаемых элементах момент внешних сил от расчетных нагрузок; во внецентренно сжатых н внецентренно растянутых элементах — момент внешней Продольной силы относительно той же осн, т. е. M=Ne (Е—расстояние от силы N до центра тяжести растянутой арматуры, см. рнс. 11.10); Ss— статический момент площади бетона сжатой зоны относительно той же оси; г, — расстояние между центрами тяжести растянутой н сжатой арматуры.
Ms
Рис. 11.10. К расчету прочности сеченнй любой симметричной формы
1 — изгибаемых; 2 — внецентренно сжатых; 3 — внецентренно растянутых
Напряжение в напрягаемой арматуре, расположенной в зоне, сжатой от действия нагрузок, Asc=Rsc—Osp определяют по значению, вычисленному при коэффициенте точности напряжения у3р, большем единицы. В элементах без предварительного напряжения ASc—Rsc-
Высоту сжатой зоны х для сечений, работающих по случаю 1, когда в растянутой арматуре и сжатом бетоне достигнуты предельные сопротивления, определяют из уравнения равновесия предельных усилий
RbAb + o„Atp-RtAtp±N = 0,
(П.40)
Где Аь — площадь бетоиа сжатой зоны, зависящая от высоты сжатой зоны; для прямоугольного сечення Аь — Ьх.
В уравнении (11.40) принимается знак «—» прн вне- центренном сжатии, знак « + » при внецентренном растяжении и yV=0 при изгибе.
Высоту сжатой зоны х для сечений, работающих по случаю 2, когда разрушение происходит пр сжатому бетону хрупко, а напряжения в арматуре предельного зна - I чення не достигают, также определяют из уравнения
. Но в этом^ случае расчетное сопротивление Rs Заменяют напряжением as.
На основе анализа результатов большого числа экспериментов установлено, что напряжение <т« зависит от относительной высоты сжатой зоны —xlho оно может определяться по эмпирической формуле
As = - lubh—(JL - i + asP. (11.41)
S 1 — (cd/1 ,1) V i SP '
В формуле (11.41) <A=X0/Ho— относительная высота сжатой зоны прн напряжении в арматуре as=aSp (или <Ts=0— в элементах без предварительного напряжения).
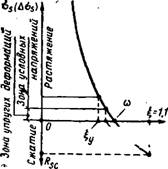
Поскольку при Os — Osp (или при <Ts=0) фактическая относительная высота сжатой зоны £ = 1, то со может рас - - сматриваться как. коэффициент полноты фактической эпюры напряжений в бетоне при замене ее условной прямоугольной эпюрой; при этрм усилие бетона сжатой зоны Nb=(j>bh0Rb (рис. 11.11). На основе опытных данных установлено, что для тяжелого бетона о>=0,85—0,008/?»; для бетонов на легких заполнителях со=0,8—0,008#г>.
Значение ©, вычисленное по этим опытным формулам, называется характеристикой двформативных свойств бетона сжатой зоны.
В формуле (П.41) первый член правой части представляет собой приращение напряжения Aas в напрягаемой арматуре или напряжение as в арматуре элементов без предварительного напряжения. Если относительная высота сжатой зоны £<со, напряжение <rs будет растягивающим, если же £>©,— сжимающим (рис. 11.12).
Граничная относительная высота сжатой зоны = —Xyjho, при которой растягивающие напряжения в арматуре начинают достигать предельных значений Os-+-Rs, Может быть найдена из зависимости (11.41)
Ъу = ю/[1 + (o-sl/o-s2)(l -(0/1,і), (11.42)
Где a<i=/?s — агр— напряжение в арматуре с фнзнческнм пределом текучести нли
O-Sl = Rs + 80,2 ES — Osp (II.43)
— напряжение в арматуре с условным пределом текучести с учетом накопившихся остаточных деформаций ео. г, поскольку в завнснмостн
Предполагается, что в арматуре развились только упругие деформации (рнс. 11.13).
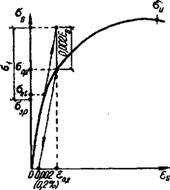
Рис. 11.13. К определению Oi — условного предельного напряжении в арматуре, не имеющей физического предела текучести
В расчетах сечений принимают е0,2£«=400 МПа; as2—RubEs — 400 МПа (исходя из предельной сжимаемости бетона 0,002); os2=eUbЈs = 500 МПа при коэффициенте условий работы бетона y&2<1 (когда при длительном действии нагрузки предельная сжимаемость бетона увеличивается и достигает 0,0025).
Если напряжения о*,'вычисленные по формуле (11.41) для арматуры, не имеющей физического предела текучести, превышают предел упругости 0«>=О,8 и находятся в интервале ase<Os^Rt, значение о* должно уточняться расчетом по формуле
= (11.44)
Для расчета прочности внецентренно сжатых элементов в нормах приводится другая упрощенная зависимость по определению граничной высоты сжатой зоны.
Таким образом, в общем случае расчет прочности сечения, нормального к продольной оси, производится в зависимости от значения относительной высоты сжатой зоны. Если Уг высота сжатой зоны определяется из уравнения (11.40), если же 1>1У, высота сжатой зоны определяется из совместного решения уравнения (11.40) и зависимости (11.41). При этом несущая способность в обоих случаях устанавливается по условию (11.39).
Напряжения высокопрочной арматуры as в предельном состоянии могут превышать' условный предел текучести. По данным опытов, это может происходить, если относительная высота сжатой зоны, найденная из уравнения (11.40), меньше граничной, т. е. 1<1У. Превышение оказывается тем большим, чем меньше значение Опытная зависимость имеет вид
= 0,95 — (о,95 —^ — 1 ) . (11.45)
Rs 0(|,2 ст0,2 / 1у
В расчетах прочности сечений расчетное сопротивление арматуры RB умножают на коэффициент условий работы арматуры yse
Т* = Я-(Ч-1)(2Б/6,-1), (И-46)
Где г] —принимают равным:
TOC o "1-3" h z для арматуры классов A-IV, At-IVC 1,2
То же, A-V, Ат-V, B-II, Вр-ІІ, К-7, К-19 . ... 1,15
» А-VI, At-VI 1,1
| определяют прн этом, полагая y»e= 1. *