Призмениая прочность бетона при сжатии
Железобетонные конструкции по форме отличаются от кубов, поэтому кубиковая прочность бетона не может быть непосредственно использована в расчетах прочности элементов конструкции. Основной характеристикой прочности бетона сжатых элементов является призменная прочность Rb — временное сопротивление осевому сжатию бетонных призм. Опыты на бетонных призмах с размером стороны основания а и высотой H показали, что приз - меиная прочность бетона меньше кубиковой и что она уменьшается с увеличением отношения H/A. Кривая, приведенная на рис. 1.5, иллюстрирует зависимость отношения Rb/R от H/A по усредненным опытным данным. / Влияние сил трения на торцах призмы уменьшается с увеличением ее высоты и при отношении H/A—А значение Rb становится почти стабильным и равным примерно 0,75 R. Влияние гибкости бетонного образца при Этих испытаниях не сказывалось, так как оно ощутимо лишь при ft/a3s 8.
В качестве характеристики прочности бетона сжатой зоны изгибаемых элементов также принимают Rb, при этом вместо действительной криволинейной эпюры напряжений бетона сжатой зоны в предельном состоянии принимают условную прямоугольную эпюру напряжений (рис. 1.6).
Прочность бетона при растяжении зависит от прочности цементного камня при растяжении и сцепления его с зернами заполнителей. Согласно опытным данным, прочность бетона при растяжении в 10—20 раз меньше, чем при сжатии, причем относительная прочность прн растяжении уменьшается с увеличением класса бетона. В опытах наблюдается еще больший по сравнению со сжатием разброс прочности. Повышение прочности бетона при растяжении может быть достигнуто увеличением расхода цемента, уменьшением W/C, применением щебня с шероховатой поверхностью.
Временное сопротивление бетона осевому растяжению можно определять по эмпирической формуле
Вследствие неоднородности структуры бетону. эта формула не всегда дает правильные значения Rbt. Значение Rbt определяют испытаниями на разрыв образцов в виде восьмерки, на раскалывание образцов в виде цилиндров, на изгиб — бетонных балок (рис. 1.7). По разрушающему моменту бетонной балки определяют
Rbt = M/YW = 3,5AJ/M?, (1.3)
Где W=Bh!/6 — момент сопротивления прямоугольного сечения; у= = 1,7 — множитель, учитывающий криволинейный характер эпюры напряжений в бетоне растянутой зоны сечеиия вследствие развития неупругих деформаций.
Прочность бетона при срезе и скалывании. В чистом виде явление среза состоит в разделении элемента на две части по сечению, к которому приложены перерезывающие силы. При этом сопротивление срезу зерен крупных заполнителей, работающих как шпонки в плоскости среза, оказывает существенное влияние. При срезе распределение напряжений по площади сечения считается равномерным. Временное сопротивление бетона при срезе можно определять по эмпирической формуле
Rsh = 0jV Rb Rbt Или Rsh = 2Rbi. (1.4)
В железобетонных конструкциях чистый срез встречается редко; обычно он сопровождается действием продольных сил.
Сопротивление бетона скалыванию возникает при изгибе железобетонных балок до появления в них наклонных трещин. Скалывающие напряжения по высоте сечения изменяются по квадратной параболе. Временное сопротивление скалыванию при изгибе, согласно опытным данным, в 1,5—2 раза больше Rbt.
Прочность бетоиа при длительном действии нагрузки. Согласно опытным данным, при длительном действии нагрузки и высоких напряжениях под влиянием развивающихся значительных неупругих деформаций и структурных изменений бетон разрушается при напряжениях, меньших, чем временное сопротивление осевому сжатию Rb. Предел длительного сопротивления бетона осевому сжатию по опытным данным может составлять Rbt = =0,90 Rb и меньше. Если при эксплуатации конструкции в благоприятных для нарастания прочности бетона условиях уровень напряжений Ob/Rbi постепенно уменьшается, отрицательное влияние фактора длительного загру - жения может и не проявляться.
Прочность бетоиа при многократно повторных нагрузках. При действии многократно повторных нагрузок с Повторяемостью в несколько миллионов циклов временное сопротивление бетона сжатию под влиянием развития структурных микротрещии уменьшается. Предел прочности бетона при многократно повторных нагрузках или предел выносливости бетона Rr, согласно опытным данным, зависит от числа циклов нагрузки и разгрузки и отношения попеременно возникающих минимальных И
О 0,2 0,4 0,6 0,в 1 Р - &Mlnfomax
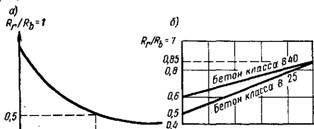
Рис. 1.8. Зависимость предела прочности бетона
А — от числа циклов за - груженин п; б — от характеристики цикла на базе п=2-Ю6; в —к определению коэффициента динамической прочности бетона
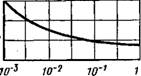
Максимальных напряжений или асимметрии цикла р = = 0min/0max. На кривой выносливости (рис. 1.8, а) по оси абсцисс отложено число циклов п, а по оси ординат — значение изменяющегося периодически предела выносливости бетона Rr. С увеличением числа циклов п снижается Rrl напряжение на горизонтальном участке кривой при п-*-оо называют абсолютным пределом выносливости. Практический предел выносливости Rr (на ограниченной базе п=2-Ю6) зависит от характеристики цикла р почти линейно, его наименьшее значение Rr = = 0,5 Rb (рис. 1.8, б).
Наименьшее значение предела выносливости, как показывают исследования, связано с границей образования структурных микротрещин так, что Rr^Rcr. Такая связь между Rr и Rcr позволяет находить предел выносливости по первичному нагружению образца определением границы образования структурных микротрещин ультразвуковой аппаратурой.
2- 10s Число циклов, п
Значение Rr необходимо для расчета на выносливость железобетонных конструкций, испытывающих динамические нагрузки, — "подкрановых балок, перекрытий некоторых промышленных зданий и т. п.