Моделирование миграции подземных вод
Составление теоретических гидрогеомиграционных моделей
Представим в свободном виде общие теоретические модели миграционных процессов, реализующие рассмотренные выше концепции о различных гидрогеомиграционных (геомиграционных) процессах на системных (кибернетических) позициях.
Базовым для построения гидрогеомиграционных моделей является балансовое уравнение переноса мигранта, которое составляют при следующих предположениях:
|
Рис. 13. Трехступенчатая система |
— среда имеет изотропное гетерогенно-блоковое строение, т. е. состоит из квазиоднородной системы относительно слабопроницаемых блоков (включающих также иммобильную воду), равномерно прорезаемых проводящими каналами (см. гл. 4), причем каналы и блоки являются полностью водонасыщенными;
— перенос осуществляется конвективным путем и дисперсией, следующей закону Фика (4.3). Для удобства описания дисперсии представим это уравнение в координатах гидродинамической сетки, обозначив через I направление линий тока и через т направление линий равного напора (в изотропной среде эти направления будут ортогональны).
Баланс мигранта с концентрацией с в жидкой фазе включает члены, характеризующие различные стороны гидрогеомиграцион - ного процесса; 1) конвективный перенос плотностью[9] uK=cv;. 2) продольную и поперечную дисперсию плотностью, соответственно,
Udtl = —Dt (дсіді) и ua, т——DT(dc/dт),
Где Di и От — коэффициенты продольной и поперечной дисперсии, [см. уравнения (4.2) и (4.5)]; 3) изменения миграционной емкости в жидкой и твердой фазах проводящих каналов, которые в единице объема среды (репрезентативного элемента) имеют, соответственно, выражения щ(dcjdt) и %(dNjdt), где пj— удельная емкость каналов, % — удельное (в единице объема породы) содержание каналов, N — сорбционная емкость твердой фазы породы в каналах; 4) обмен мигранта между каналами и блоками, характеризующийся скоростью удельного (в единице объема породы) перехода мигранта в блоки и*; 5) превращения мигранта в водной среде каналов, характеризующиеся удельной (в единице объема) скоростью реакций R.
Из этих членов составляется балансовое уравнение:
Дс, dN. * . п, де д і ~ дс \ . д (^ дс \ ... с і ч
Й>V+ ■ •ТГ + ■"+ ■R +0 -ЗГ - IF (■іг) +1Г (А <5Л >
Входящие в него скорости фильтрации v находятся из решения геофильтрационной задачи, которое во многих случаях может быть получено предварительно, независимо от гидрогеомиграционной задачи. Поэтому изучение переноса мигрантов должно начинаться с обстоятельного анализа геофильтрационной модели, на основании которой строится поле скоростей потока. Для правильного понимания геофильтрационной обстановки целесообразно предварительно построить схему потока [9, 38], на которой фиксируются зоны питания и разгрузки, с нанесением всех известных данных о балансовых элементах потока в этих зонах.
На основе геофильтрационной схемы (модели) строится гидродинамическая сетка, по которой рассчитываются величины скоростей и направление течения в области возможного распространения мигранта. Специфическим для миграционных расчетов является повышенная требовательность к построению линий тока, что в некоторых случаях (например, при наличии скважин, еозда-
ющих зоны с резкой деформацией потока) требует применения специальных методических приемов (см. гл. 6).
Кроме того, при существенном различии плотностей в различных областях потока приходится учитывать плотностную конвекцию, что требует совместного решения задач переноса и фильтрации подземных вод, поскольку в этом случае скорости фильтрации будут зависеть от распределения плотности жидкости, связанной с концентрацией мигрантов. Практически можно считать, что для данного типа воды плотность р практически однозначно связывается с общей минерализацией с линейной зависимостью вида (1.1) — (1.3). Для решения миграционных задач, как правило, не требуется учета сжимаемости пласта, так что уравнение неразрывности водного потока записывается в форме divo=0. Подставляя в это уравнение выражения для компонентов скоростей фильтрации, получим дифференциальное уравнение пространственного фильтрационного потока
Д F kx дН \ д д
Дх \ р дх J ду ду J dz
Где р=р/р0 —относительная плотность, причем величина р0 задается для пресных вод и для некоторой средней в рассматриваемой области потока; Н=р/ (p0g-}-z)—напор усредненного потока, соответствующего некоторой постоянной плотности р0. Уравнения (5.1) и (5.2) с соотношением р(с) составляют замкнутую систему, решение которой при определенных краевых условиях позволяет провести фильтрационно-миграционный расчет потока с переменной плотностью.
Заметим, что если изменение содержания мигранта в твердой фазе обусловливается процессами ионного обмена, то при записи исходного уравнения переноса (5.1) суммарной концентрации (минерализации) относительно величины ст в нем пропадает член dNjdt, поскольку суммарное содержание вещества в твердой фазе при ионном обмене остается равным емкости поглощения.
Особый случай при этом составляют потоки «усочно-перемен - ной плотности, возникающие, например, при интрузии морских вод или формировании линз пресных вод, когда следует также учитывать условия разрыва напоров на границах зон с различной плотностью (см. гл. 7).
Для учета макродисперсии, обусловленной гетерогенностью породы и пласта в пределах репрезентативного элемента потока, используются две основные расчетные схемы (модели): диффузионная и гетерогенно-блоковая (см. гл. 4).
В диффузионной модели среда предполагается квазигомогенной (без выделения каналов и блоков), когда в общем дифференциальном уравнении (5.1) пренебрегают членом и*, считают %=1, а макродисперсия описывается членами правой части этого уравнения при коэффициентах дисперсии Di и DT, некоторым образом зависящими от скорости фильтрации v. В практических целях обычно
принимается [8, 15, 37], что эти зависимости аналогичны установленным для гидродисперсии, т. е. для Di и Dr считаются справедливыми выражения (4.7), (4.11). Как отмечалось в выражении (4.5), зависимость параметров дисперсии от хода процесса отражает принципиальную неравномерность безоговорочного перенесения моделей процессов, протекающих на микроуровне, поскольку столь сильные количественные изменения масштаба процесса диалектически должны приводить к качественным преобразованиям в используемых теоретических моделях переноса. В связи с этим для описания процессов макродисперсии целесообразно использовать модель гетерогенно-блоковой среды [см. уравнение (4.3)], в которой неоднородность строения породы учитывается в непосредственной и наглядной форме. При этом в правой части выражения (5.1) исключается член продольной дисперсии (£)/ — 0), а коэффициент поперечной дисперсии DT задается, например, согласно выражению (4.39). Продольная дисперсия учитывается внутриблоко - вым обменом, причем форма члена и* задается исходя из принятой схемы переноса мигрантов внутри блоков. Согласно изложенным в гл. 4 положениям, гетерогенно-блоковая среда считается состоящей из проводящих каналов с удельной емкостью пх = пк: и из блоков с сосредоточенной и неограниченной емкостью.
Скорость блокового обмена и* — и0* для схемы сосредоточенной емкости блоков определяется выражением
Дс^
Tl0* — (1 — х) п* —■ — а* (с -- <Г:),
Где с* — расчетная концентрация мигранта в блоках; а* — коэффициент блокового обмена, определяемый выражением (4.12). Для схемы неограниченной емкости блоков величина и*—и** определяется выражением (4.14).
Можно также рассматривать комбинированную гетерогенно - блоковую модель, составляемую из блоков с сосредоточенной и неограниченной емкостью.
При использовании модели гетерогенно-блоковой среды слоистость пласта в явном виде учитывается при миграционной схематизации, исходя из принятого геофильтрационного разреза. Такой подход к описанию процессов переноса по сравнению с «диффузионной» моделью отличается следующими достоинствами: 1) в нем ясно отражается физическая сущность процесса макродисперсии и параметры модели связываются с независимо измеряемыми характеристиками породы и пласта (размеры и удельная поверхность блоков, мощность и проницаемость слоев); 2) сохраняется возможность использования расчетной модели при переменной скорости фильтрации, в том числе при остановке и изменении направления переноса, тогда как задание параметров дисперсии в диффузионной модели в таких случаях становится неопределенным. Эти достоинства дают основания считать модель гетерогенно-блоковой модели с непосредственным учетом слоистости пластов более предпочтительной, чем «диффузионная» модель дисперсии мигрантов.
Такая позиция, разумеется, не исключает возможности применения «диффузионной» модели, однако ее использование целесообразно существенно ограничить условиями, при которых оно дает какие - либо преимущества.
|
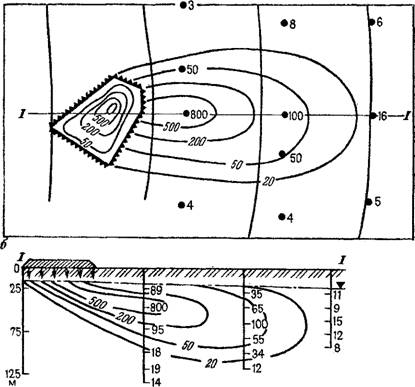
Рис. 14. Распространение загрязняющего мигранта нз хвостохранилища в плане (а) и в разрезе (б) [36]. |
|
1,2 — хвостохранилнще в плане и разрезе, соответственно; 3 — скважины и содержание мигранта (в мкг/л); 4, 5 — гидронзогипсы и изолиний содержания мигранта (в мкг/л); 6 — уровень грунтовых вод; 7 — место отбора пробы и содержание мигранта (в мкг/л) |
Заметим, что в ряде случаев представление о значительной гидродинамической дисперсии может быть кажущимся, что объясняется влиянием на условия переноса других факторов и процессов. Пример такой ситуации приведен на рис. 14, где показаны изолинии минерализации грунтовых вод при фильтрации загрязняющих веществ из хвостохранилища. На плане потока (см. рис. 14, а) видно, что поперечная дисперсия загрязнения в плане в значительной степени является кажущейся, поскольку она обусловливается
А
неравномерностью распределения исходной минерализации загрязняющих растворов в самом хвостохранилище. Что касается дифференциации загрязнения по вертикали (см. рис. 14,6), то оно прежде всего связано (особенно в верхней части потока) с интенсивным инфильтрационным питанием, поступающим на поверхность грунтовых вод с расположенных здесь орошаемых территорий, и плотностной конвекцией.
Математические модели обмена в системе «вода—порода» основаны на термодинамических представлениях о физико-химических процессах, происходящих на границах твердой и жидкой фаз (см. гл. 3). Для записи этой модели в таких же величинах, что и модели переноса, в качестве Характеристики термодинамического потенциала р.» (см. гл. 6) используется концентрация мигранта в жидкой фазе Сі. Удельное содержание мигранта в твердой фазе Ni связывается при этом системой уравнений равновесного состояния и кинетики процесса (см. гл. 3).
Для практических расчетов при сравнительно гомогенном строении горных пород обычно можно не учитывать кинетику сорбции (обоснование этого положения см. в гл. 6). В этом случае величина N связывается с концентрацией с изотермой сорбции и dN/dt= ~Kd(dcjdt), где Kd—dN/dc — коэффициент распределения, который в общем случае зависит от концентрации с в соответствии с изотермой сорбции, а в частности при использовании линейной изотермы (31) величина Kd будет постоянной. Влияние сорбцион - ной емкости на процессы переноса при этом может формально учитываться заменой в уравнении (5.1) величины щ на эффективную пористость (удельную емкость) пэ породы по отношению к данному мигранту, определяемую выражением
Пэ = п0 + Ка. (5.3)
Величина «э (или Kd) является важнейшим миграционным параметром, определение которого требует очень внимательного обоснования, поскольку он может существенно зависеть от всего ма - крокомпонентного состава мигрирующего раствора.
В гетерогенной среде обменные процессы развиваются главным образом в слабопроницаемых блоках, где на их кинетику может существенно влиять доступность воде мигрантов, находящихся в твердой фазе. Для модели гетерогенно-блоковой Среды с сосредоточенной емкостью уравнение внутриблоковоґо обмена с учетом ионного обмена имеет вид
Я„<£ +а^ (54)
Dt at
Где с* — концентрация мигранта в жидкой фазе; N* — удельное содержание мигранта в твердой фазе блоков; а* — коэффициент блокового обмена, определяемый выражением (4.13). Уравнение (5.4) должно решаться вместе с уравнением кинетики ионного обмена, при записи которого полагается N=N*. Заметим, что в гетерогенных породах возможность не учитывать кинетику обменных процессов становится значительно более проблематичной, поскольку мигранты в твердой фазе могут быт> «запечатаны» слабопроницаемыми оболочками, уменьшающими их доступность для обмена с жидкой фазой.
Для многокомпонентной системы мигрантов, участвующих в обменных процессах, уравнение переноса (5.1) записывается для каждого мигранта, а связь между ними задается условиями электронейтральности и постоянства суммарной емкости поглощения с учетом закона действующих масс (см. гл. 8).
При учете гидрохимических превращений, исходя из теории химических реакций (см. гл. 2), записываются, кроме того, выражения для скорости удельных превращений R в водной фазе, причем для гетерогенной среды в левой части уравнения (5.4) также добавляется член R скорости удельных превращений в блоках.
Особой проблемой является оценка изменений проницаемости породы, происходящих при обмене и превращениях. Пока такие оценки возможны лишь на основе эмпирических данных [7, 12]. Следует подчеркнуть, что учет обмена и превращений в теоретических моделях нередко представляет собой чрезвычайно сложную задачу, решение которой является делом будущего.