ХИМИЯ КРЕМНЕЗЕМА

Размер частиц и упаковка

В течение многих лет структура силикагелей оставалась предметом дискуссий. Структура геля зачастую представлялась в виде сетки с поперечными связями, составленной из молеку­лярных «цепочек» поликремневой кислоты, подобно структуре органических гелей. Однако в 1926 г. Френдлих предложил, а в 1940 г. Кармен обосновал предложение рассматривать структуру силикагеля как состоящую из первичных сфериче­ских частиц.

До того как была открыта возможность приготовлять од­нородные частицы кремнезема с диаметром больше 5—10 нм, силикагели получались из типов кремнезема, сформирован­ных в результате подкисления силиката натрия или гидролиза сложных кремневых эфиров. Даже с помощью электронного микроскопа было трудно различить структуру таких гелей. Од­нако из рассмотрений Айлера [2], Киселева [3], Высоцкого (в работе [5]) и Унгера [6], несомненно, следует, что силика­гели и кремнеземные порошки первоначально образуются из «корпускулярных» или «глобулярных» дискретных частиц. Шу - гар и Губа [125] разработали способ приготовления тонких срезов из очень тонкодисперсных структур геля, что позволило получить снимки с 105-кратным увеличением. Благодаря этому удалось различить, что структура в действительности представ­ляла собой подобные волокнам нити, состоящие из цепочек гло­
бул. Были измерены размеры пор и диаметров частиц и подсчи­таны значения удельной поверхности и среднего размера пор, которые удовлетворительно согласовывались со значениями, полученными по адсорбции азота. Леонтьев и Лукьянович [126а] при проведении электронно-микроскопических исследований раз­личных кремнеземов использовали метод углеродных реплик, получаемых со структур силикагелей.

Образование цепочек из частиц кремнезема сферической формы в структуре геля было подробно рассмотрено в гл. 3. В данном разделе описывается влияние, оказываемое на пори­стость размерами частиц и их упаковкой.

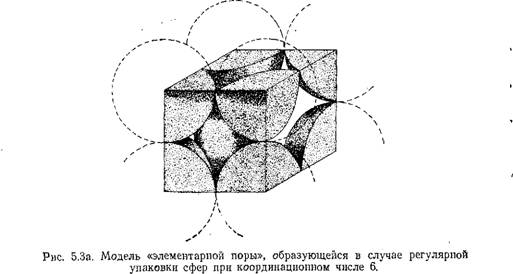
Модель типичной поры в компактном силикагеле с кубиче­ской упаковкой сферических частиц показана на рис. 5.3а. Объем пор составляет 48 % от общего объема. Поскольку 52 % приходится на объем самого кремнезема, который имеет плотность 2,2 г/см3, то удельная пористость оказывается равной 0,42 см3/г.

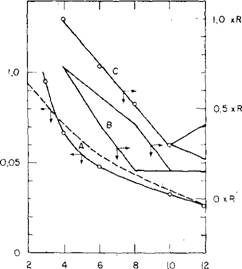
Еще в 1954 г. Киселев [1266] подсчитал значения удельной поверхности, объемов пор, размеров пор, а также координацион­ное число средней частицы в зависимости от изменения плот­ности упаковки таких сферических частиц. Как видно из рис. 5.36, если геометрия упаковки остается без изменений, то диаметр пор убывает с уменьшением диаметра частиц. С дру­гой стороны, при изменении упаковки частиц постоянного раз­мера диаметр пор может изменяться. К тому же оба фактора — упаковка и размер частиц—могут изменяться одновременно таким образом, что диаметр пор сохраняется постоянным.

На основании экспериментальных данных считается, что все гели и осажденные кремнеземы имеют тенденцию сжиматься под действием сил поверхностного натяжения воды, определяющих усадку по мере того, как вода удаляется при высушивании из пор. Если не принимать специальных мер предосторожности, чтобы укрепить структуру и понизить влияние сил поверхност­ного натяжения, то образовавшийся влажный осадок, или гель, оказывается сильно уплотненным до приблизительно одного и того же координационного числа, равного 5—6. В этом случае диаметр пор пропорционален размеру частиц и изменяется об­ратно пропорционально величине удельной поверхности. Унгер [6] дает следующую взаимосвязь диаметра пор по данным Ду­бинина и удельной поверхности:

Удельная поверхность, м'/г

Рис. 5.36. Схемы структур с различной пористостью. Размеры первичных частиц и координационное число (число частнц, касающихся каждой единичной частицы) определяют объем пор и их средний диаметр. В действительности структуры трехмерны. 1 — объем твердого вещества; 2 — объем пор.

Однако такая связь не всегда существует; так, в некоторых рыхлых аэрогелях, имеющих очень низкую плотность, могут быть и поры большого диаметра, и высокие значения удельной поверхности.

Взаимосвязь размеров частиц и их упаковки с характеристи­ками пор рассматривалась на примерах нескольких моделей. Масон [127] рассмотрел произвольную упаковку сфер, поскольку в силикагелях упаковка, конечно, не является регулярной (за исключением опала, который обсуждался в гл. 4). Он рассмат­ривал пору в виде тетраэдрического узла, в котором центры соседних сфер соединены, хотя при этом сферы не обязательно касаются друг друга. Поры, следовательно, определяются коор­динатами центров сфер. Свойства таких пор оценивались на ЭВМ по составленной программе. Согласно Масону, произволь­ная упаковка сфер дает объемную плотность, равную 0,63, что оказывается примерно средним значением между значением 0,52, характерным для открытой (кубической) упаковки, и значением 0,72 для закрытой (гексагональной) упаковки.

Упаковка частиц изучалась экспериментально, начиная с очень тонкодисперсных кремнеземных порошков, состоящих из однородных по размеру частиц и находящихся в рыхлом состоянии с низким значением объемной плотности, когда каж­дая единичная частица касается только лишь двух, трех или четырех соседних частиц. Когда же такая система механически спрессовывается, то число контактов между частицами стано­вится все больше и больше.

Были подсчитаны [128] адсорбционные характеристики и геометрия упакованных сферических частиц. Используя коор­динационные числа 4, 6 и 8, авторы этой работы вывели урав­нение для подсчета количества вещества, адсорбированного при различных значениях относительных давлений.

Эвери и Рамзай [129] также подсчитали характеристики различных способов упаковки однородных по размеру сфер, представленные в табл. 5.1. Хотя в действительности в гелях, ве­роятно, отсутствует подобная регулярность упаковки, тем не менее из данных по пористости геля можно оценить значение координационного числа п. Если средний диаметр частиц изве­стен, то по плотности геля можно приблизительно подсчитать диаметр пор. При этом заранее предполагается, что все пер­вичные частицы в геле однородны по размеру, и это в общем оказывается справедливым, если только не принимаются особые условия, позволяющие иметь в системе частицы двух размеров.

Мейсснер, Михаэле и Кайзер [130] рассмотрели другие рас­положения упаковок при значениях доли </>, приходящейся на твердую фазу ([1—ф]—доля, относящаяся к пористости), подсчитанной для разных координационных чисел. Авторы ссы - дались на ранее выполненные работы Хиша и Лавеса [131] и Манегольда, Хоффмана и Соффа [132] с приблизительно та-

Ким же общим подходом. Мейсснер предложил общее урав­нение

П = 2 ехр {2,4ф)

Для которого были подсчитаны некоторые величины, представ­ленные на рис. 5.4. При этом доля объемной пористости при­нимается равной 1 —ф.

Чтобы более точно смоделировать действительные структуры гелей, целесообразно провести исследования плотно, но произ­вольно упакованных сфер. Скотт [133] сообщает, что при рых­лой произвольной упаковке однородных сфер значение объем­ной плотности равно 0,60, тогда как при плотной произвольной

Упаковке получается значение 0,64. Эти результаты обсужда­лись Берналом, Масоном и Найтом [134, 135]. Действие, ока­зываемое произвольной упаковкой сфер на капиллярные свой­ства системы, было описано Масоном [127].