ЮВЕЛИРНОЕ ДЕЛО

СПЛАВЫ БЛАГОРОДНЫХ МЕТАЛЛОВ

Для того чтобы получить новые необходимые свой­ства изделий, например более высокую прочность или пластичность, пользуются сплавами благородных метал­лов с другими металлами. Такие сплавы называются ле­гированными. Важно, что при этом экономятся дорогие благородные металлы, так как в качестве легирующих

Элементов используются более дешевые металлы (се­ребро, медь, никель, цинк и др.). Одновременно достига­ется и разнообразная цветовая окраска сплавов в соот­ветствии с современной модой (табл. 2).

Вычисление проб и лигатур. Сплавы благородных металлов, из которых изготовляются ювелирные изде­лия, должны своей пробой, т. е. содержанием чистого металла в сплаве, соответствовать действующим пред­писаниям. Важно в совершенстве овладеть умением вы­числять пробы для того, чтобы, с одной стороны, уметь приготовить лигатуры различных сплавов, а с другой — рационально использовать благородные металлы.

Приходится также часто встречаться с необходи­мостью повысить или снизить пробу (перевод опреде­ленной пробы в пробу, установленную законом) или подсчитать среднюю пробу нескольких слитков. Для этих целей служат разные пересчетные таблицы, кото­рых, однако, для всех случаев в практике должно было бы быть великое множество, и на то, чтобы отыскать нужные пробы и массу, потребовалось бы больше вре­мени, чем на своевременное и точное вычисление.

Приведенные примеры из практики служат руковод­ством и образцом таких вычислений (проба пишется са­мой простой десятичной дробью, например, 585 тысяч­ных—0,585).

1. Необходимо подсчитать, сколько чистого металла содержится в сплаве, если проба сплава известна.

Надо определить массу сплава (или предмета) и по­лученные данные умножить на пробу.

Пример а. Сколько чистого золота содержится в 25,6 г сплава 0,750 пробы?

25,6-0,750 = 19,20. В 25,6 г золота 0,750 пробы содержится 19,20 г чистого золота.

Пример 6. Сколько чистого серебра содержится в 1520 т сплава 0,835 пробы?

1520-0,835=1269,20. В 1520 г сплава 0,835 пробы содержится 1269,20 г чистого серебра.

Пример в. Сколько чистой платины содержится в 8,45 г сплава 0,680 пробы?

8,45-0,680=5,746. В 8,45 г сплава 0,680 пробы содержится 5,746 г чистой платины.

2. Из чистого металла необходимо сделать сплав определенной пробы.

Пример а. Сколько золота 0,585 пробы получится из 14,50 г чи­стого золота?

Умножаем массу чистого металла на 1000, а результат делим на пробу, которую хотим получить:

14,50-1000/585=24,786. Из 14,50 г чистого золота получается 24,786 г золота 0,585 пробы. С последним незначительным остатком на практике не считаются и количество округляется с понижением на пять сотых грамма.

Пример б. Какова масса сплава серебра 0,800 пробы, состояще­го из 500 г чистого серебра?

500-1000/800=625. Сплав серебра 0,800 пробы будет иметь массу 625 г.

3. Сплав более высокой пробы необходимо перепла­вить в сплав государственной пробы.

Массу сплава умножаем на его пробу (результат равняется массе чистого металла в сплаве) и делим на пробу, которую хотим получить.

Пример а. Имеется 10,14 г золота 0,900 пробы, а необходима проба 0,585. Сколько примеси надо добавить?

10,14-0,900/0,585 = 15,60. Итого получаем 15,60 г золота 0,585 пробы; разница между общей массой сплава 0,585 пробы и первоначальной массой золота 0,900 пробы составляет необходимое количество примеси: 15,60—10,14= =5,46.

К 10,14 г золота 0,900 пробы прибавляем 5,46 г примеси (в про­порции соответственно требуемого цвета сплава) и при общей мас­се 15,60 г получаем в данном случае 0,585 пробу.

Пример б Из 480 г серебряных монет 0,900 пробы требуется изготовить сплав с содержанием 0,800 серебра. Сколько меди надо прибавить?

480-0,900/0,800=540. Надо прибавить 60 г меди.

4. Низкую пробу необходимо обогатить более высо­кой пробой, чтобы получить среднюю пробу.

Пример а. Сколько золота 0,900 пробы надо прибавить к 46 г золота 0,560 пробы, если требуется получить сплав 0,585 пробы?

От пробы, которую мы хотим получить, вычитаем более низкую пробу, которую имеем: 585—560=25. Этот остаток умножаем на

Массу 25-46=1150.

Из пробы, которую используем для обогащения, вычитаем пробу, которую желаем получить: 900—585=315.

Разделим: 1150/315 = 3,65.

К 46 г золота 0,560 пробы надо прибавить 3,65 г золота 0,900 пробы, получится всего 49,65 г золота 0,585 пробы.

Убедимся в том, что вычисление сделано правильно.

В 46,00 г золота 0,560 пробы содержится 25,760 г чистого зо­лота, в 3,65 г золота 0,900 пробы содержится 3,285 г чистого золота, тогда в 49,65 г золота 0,585 пробы будет 29,045 г чистого золота.

Эту задачу можно решить также другим способом: от пробы, которую мы хотим получить, вычитаем низшую пробу, которую дол­жны повысить, и результат делим на разность между более высокой пробой и пробой, которую необходимо получить. Результат равен количеству примеси на 1 г.

Примерб. Из сплава золота весом 192 г 0,520 пробы надо полу­чить сплав 0,750 пробы. Сколько чистого золота следует добавить?

(750—520)/ (1000—750) = 230/250 = 0,92 г.

0,92 • 182 = 176,64; 192,00 +176,64=386,64. К 192 г золота 0,520 пробы надо прибавить 176,64 г чистого золота и сплав 0,750 пробы будет иметь общую массу 368,64 г.

Проверим правильность решения:

, 192,00-0,520=99,84

176,64-1,000=176,64

368,64-0,750=276,48 (г чистого золота).

5. Высокую пробу надо расплавить более низкой пробой, чтобы получить среднюю пробу.

Пример. Сколько золота 0,250 пробы надо прибавить к 14 г зо­лота 0 750 пробы, если требуется получить сплав 0,585 пробы?

750:585

~ 585:250

165 : 336 = 0,4925; 0,495-14=6,895.

Проверим правильность решения:

.14,000-0,750=10,50

+ .6,895-0,250= 1,72

20,895-0,585=12,22

К 14 г золота 0,750 пробы надо прибавить 6,895 г золота 0 250 про­бы; в итоге получим 20,895 г золота 0,585 пробы.

6. Вычисление средней пробы нескольких слитков разных проб.

Суммарное содержание чистого металла в отдель­ных сплавах, разделенное на общую массу сплавов, дает среднюю пробу сплавов. Пример а.

І 50 г пробы 0,900=45 г чистого металла! 40 г пробы 0,750=30 г » » Т 30 г пробы 0,500=15 г » > ~ 20 г пробы 0,250=5 г » »

140 г слитка = 95 г чистого металла 95: 140=0,6785. Слиток массой 140 г будет иметь пробу 0,6785. Пример б.

Плавлением смешаем 480 г серебра 0,625 пробы с 800 г серебра пробы 0,750 и 720 г пробы 0,925. Какой пробы будет слиток?

480 г-0,625=300 г чистого серебра

+ 800 г-0,750 = 600 г » »

720 г-0,925 = 666 г > >

2000 г слитка = 1566 г чистого серебра 1566:2000 = 0,783. Слиток серебра будет иметь 0,783 пробу. Проверим правильность решения:

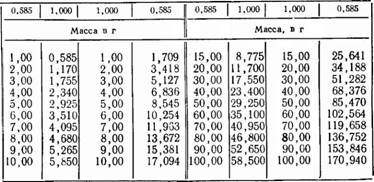
Пробу умножаем на массу: 0,783-2000=1566 г чистого серебра. Для пересчета определенной массы, например с 0,585 пробы в чистый металл или наоборот — с 1,000 в 0,585 пробу, пользуются табл. 3.

Пример а.

Сколько чистого золота содержит слиток массой 321,70 г 0,585 пробы?

+ 300,00=175,50

+ 20,00=11,70

+ 2,00 = 0,585

0,70=0,409___________

321,70=188,194

Слиток массой 321,70 г 0,585 пробы содержит 188,194 г золота. Пример б.

Сколько граммов золота 0,585 пробы дадут 27,50 г чистого золота?

+ 20,00 = 34,188

7,00=11,963

Т 0,50=0,854

27,50 = 47,005