Каталитические процессы в газах
Большую часть вырабатываемых катализаторов применяют в настоящее время для ускорения реакций в газовой (или паровой) среде. Каталитические процессы в газах проводят при самых раз
личных параметрах технологического режима-и соответственно разнообразных требованиях к физическим свойствам применяемых катализаторов: прочности, пористости, термостойкости, размерам и форме частиц и т. п.
В различных промышленных каталитических процессах температура бывает от близкой к нулю до 1200 °С, давление — от вакуума до 100 МПа, скорость газовой смеси — от нескольких сантиметров до нескольких метров в секунду; время контакта газа с катализатором колеблется от тысячных долей секунды до нескольких минут, а высота слоя катализатора изменяется от миллиметров до метров. В зависимости от условий требуются катализаторы с размерами зерен от нескольких микрометров до полутора - двух сантиметров, различной формы.
По тепловому эффекту процессы делят на экзо - и эндотермические.
|
Lопт. п Lcmm. o |
|
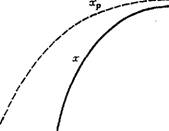
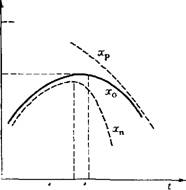
Рис. 1.7. Влияние температуры на выход продукта экзотермического обратимого процесса Выход: — равновесный; xQ — в обратимом одномаршрутном процессе; хп — целевого |
|
|
|
Продукта при наличии некаталнтнческнх побочных реакций [(т, Р, Са, Си) = const] |
Экзотермические процессы, происходящие с выделением теплоты, характеризуются наличием оптимальной температуры, соответствующей максимальному выходу продукта. Как показано на рис. 1.7, при постоянстве времени контакта т газа с катализатором, давления Р и концентраций Си, С'и исходных веществ выход продукта при возрастании температуры сначала повышается, а затем, вследствие смешения равновесия в сторону исходных веществ, снижается, обязательно проходя через максимум, соответствующий оптимальной температуре. В некоторых каталитических процессах при повышении температуры начинаются побочные реакции, и выход целевого продукта 'необратимо снижается значительно сильнее, чем по причине обратной реакции. Так происходит, например, при синтезе метанола и высших спиртов.
Рис. 1.8. Влияние температуры на равновесный (Хр) и действительный (х) выход продукта в эндотермическом обратимом процессе [(т, Р, Си, Си) = const]
Эндотермические процессы характеризуются монотонным возрастанием выхода продукта при повышении температуры (рис. 1.8). Однако и в этом случае могут возникнуть побочные реакции; поэтому выход целевого продукта (например, бутадиена при каталитическом превращении этилового спирта или бензина в процессе каталитического крекинга) может проходить через максимум, несмотря на то, что основная реакция эндотермическая.
Рациональные производственные температуры обычно ниже оптимальных для экзотермических и значительно ниже наибольших возможных для эндотермических процессов. Это объясняется тем, что при нагревании реагирующих масс уменьшается разность температур между греющими газами (жидкостями) и нагреваемыми реагентами; увеличиваются потери теплоты с отходящими теплоносителями (например, с топочными газами, а также через стенки реактора в окружающую среду). В экзотермических процессах необходимы затраты теплоты на подогрев поступающих в реактор газов до температуры зажигания катализатора t3am (наименьшей температуры, при которой начинается каталитическая реакция со скоростью, необходимой в производстве). Следовательно, весьма важно применять активные катализаторы с низким значением t3am. В эндотермических процессах поступающие газы необходимо нагревать так, чтобы компенсировать эндотермический эффект, потери теплоты и вывести газы из реактора с температурой
В ряде случаев повышение температуры ограничивается термостойкостью катализатора или реагентов и продуктов реакции. Так, при окислении диоксида серы на ванадиевых катализаторах ~ 400-^-420 °С, а самая высокая температура процесса составляет 600 °С. Дальнейшее повышение температуры приводит к постепенному огрублению структуры и падению активности катализатора. При окислении аммиака на железохромовых катализаторах верхний предел температуры ограничивается 750— 800 °С. При окислении аммиака на термостойком платиновом катализаторе возможно повышение температуры до 900 °С; дальнейшее увеличение температуры приводит к прогрессивно возрастающей диссоциации аммиака и оксида азота.
Одной из важнейших причин, ограничивающих применение высоких температур в эндотермических процессах, является низкая термостойкость сталей, из которых изготавливают трубы теплообменников-подогревателей. Углеродистые стали деформируются при t > 400—500 °С, жаропрочные — при t > 700 °С и лишь дефицитные спецсплавы выдерживают температуру до 900 °С.
По степени смешения исходных веществ с продуктами реакции различают предельные режимы идеального вытеснения и полного (идеального) смешения [19, 31—33], а также промежуточные режимы неполного смешения, характерные для производственных реакторов.
|
S |
|
А |
|
|
|
\ Исходный юз |
|
| Исходный газ |
|
Горючие |
|
Продукт-газ |
|
Продукт-газ |
|
Іорючив Т Цзы Режим идеаль- |
|
» S 1 І-* тока реагентов, при кото- |8 ром любой элемент объема Є движется по высоте (дли- |
|
(1.33) |
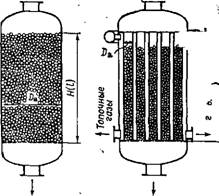
Рис. 1.9. Каталитические реакторы фильтрующего слоя в режиме работы близком к идеальному вытесне
Нию:
А — однослойный адиабатический; б — трубчатый политермический
Ного вытеснения характеризуется таким ламинарным течением по-
Не) аппарата параллельно другим элементам, не смешиваясь с предыдущими и последующими элементарными объемами [19]. Время пребывания т в ре
Акторе для всех молекул одинаково. Время пребывания любой молекулы т' равно среднему тср:
= * ср = Ф с = fi/w.
Здесь Н — высота реакционного объема.
|
(1.34) |
В контактных аппаратах с неподвижным или взвешенным (кипящим) слоем катализатора под v обычно понимают полный объем слоя катализатора, под w — линейную скорость газа, отнесенную к полному сечению аппарата, и под Я — высоту слоя катализатора. Таким образом, получают фиктивное время которое больше истинного. Для перехода от фиктивного времени пребывания газа в слое к истинному тср. и используют отношение:
"•■ср. и — Т'ф/б-
Здесь е — порозность слоя, равная vCB/v; vCB — свободный объем слоя, не занятый зернами катализатора.
К режиму идеального вытеснения приближается процесс в производственных аппаратах с неподвижным (фильтрующим) слоем катализатора при значительной высоте слоя (Я : Da 2, где Da — диаметр аппарата) и не очень больших линейных скоростях газового потока w < 1 м/с. Два типа таких реакторов представлены на рис. 1.9. При ламинарном течении газа через любой элементарный объем dv такого реактора или соответствующую ему высоту dH за время dx количество целевого продукта в газовой смеси увеличивается на dGn, соответственно концентрация продукта возрастает на dCn, а выход его — на dx. Следовательно, скорость процесса равна:
|
|
(1.35)
Принимая во внимание соотношение (1.33), можно также записать:
" = FcW или и=а)ж - ^
В технической литературе используют те или иные выражения скорости [7, 9, 17, 19—21, 31] в зависимости от того, какие из входящих в них величин известны и удобны для применения в определенных условиях [см., например, уравнения (1.3), (1.3а)]. Если замеряют Gn во времени, то наиболее удобна формула:
И = = toAC. (1.37)
Здесь v — общий или свободный объем слоя катализатора и соответственно т = Тф или т = tcd „; k — константа скорости, выражаемая уравнениями (1.4), (1.6), (1.24).
Нередко скорость процесса выражают производной концентрации Си основного исходного вещества по высоте Я слоя катализатора (или реакционного объема):
U = =kbC. (1.38)
An
Для модельной реакции синтеза ак + ЬВ = сЮ движущая сила по закону действующих масс равна:
ДС = (СА-С*А)а(Св-С*)6.. (1.39)
Здесь СА, Св — текущие концентрации исходных реагирующих веществ; С а и Св — их равновесные концентрации.
Ряд обратимых реакций еще недостаточно изучен, и определение общей константы скорости k ~ f (kly k2) и общей движущей силы АС затруднено. Поэтому общую скорость реакции и выра-
Жают разностью скоростей прямой щ и обратной щ реакций:
И — u-i — и2 = АС! — А:2АС2. (1-40)
Здесь А С, = СдСц-, А С2 = CdD.
Для необратимых реакций и обратимых вдали от равновесия принимают ДС2 = 0. Так, для прямой реакции первого порядка уравнение (1.3а) можно записать через степень превращения основного вещества х:
Dx
(,=—= МС = «(1-ї). (1.41)
Откуда
Кинетические уравнения идеального вытеснения применяют для расчета однослойных, многослойных и трубчатых реакторов с фильтрующими слоями катализатора [19, 31, 33], а также для
Г
41
Рис. 1.10. Каталитический изотермический реактор кипящего слоя с мешалкой, с режимом работы, близким к полному смешению
Реакторов с организованным (заторможенным) кипящим слоем [17, 34]. Реакторы с движущимся катализатором [7, 19] и с потоком взвеси катализатора [7] обычно рассчитывают также по формулам идеального вытеснения. Кроме того, формулы (1.35)—(1.41) применяют для расчета реакторов периодического действия.
Кинетическая модель реактора, т. е. характеристическое урав - ГІ ' ХНисходный нение. применимое для опреде-
|)0 0 О О 0 0 0(( 3 ления времени контакта т в реак-
'---------------------------- торе вытеснения для необратимой
Реакции п-ю порядка по основному веществу А, идущей без изменения объема:
X X
|
(1.43) |
|
Kcl |
|
■х)п |
Dx _ Г dx
= СА
KC\ (1
Н
Здесь Сдн — начальная (на входе в реактор) концентрация основного исходного вещества, определяющего скорость реакции.
При неизменной константе k
Х
|
(1.44) |
|
Т = |
1 Г dx
Г___ dx
|
П-1 |
|
(l-x)n |
|
KC |
J (1-
Режим полного смешения характеризуется столь турбулентным течением потока реагентов, при котором любой элементарный объем реагирующей смеси мгновенно перемешивается со всем содержимым реактора, так как скорость циркуляционных движений газа (жидкости) по высоте и сечению во много раз больше скорости линейного движения по оси реактора Время пребывания в реакторе отдельных молекул может теоретически изменяться от нуля до бесконечности и т' т^тср. В реакторах полного смешения температуры и концентрации реагентов во всем реакционном объеме постоянны.
|
Продукт - |
|
Щ |
|
■П. |
|
1л |
|
T-V ■-■ '—^XJ |
К режиму полного смешения приближаются каталитические процессы в реакторах свободного взвешенного (кипящего) слоя, не заторможенного какими-либо насадками, при не очень больших высотах слоя (Я < 1 м) и высоких скоростях газового потока, в 2—4 раза превышающих критическую скорость начала 42
взвешивания. Практически полное перемешивание достигается в аппаратах кипящего слоя, снабженных мешалкой (рис. 1.10). Сравнение типичных кривых кинетики химического процесса в реакторах вытеснения и смешения представлено на рис. 1.11.
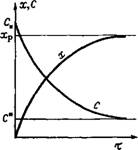
В реакторах периодического действия и проточных реакторах идеального вытеснения (рис. 1.11, а) скорость реакции непрерывно уменьшается во времени, т. е. по высоте слоя катализатора (т = = аН), поэтому кинетика и выражается дифференциальными уравнениями типа (1.37), (1.44). Среднее значение концентрации исходного вещества, определяющего АС по уравнению (1.39), выражается формулой:
Сср = (Св - С„)/[2,3 lg (Сн/Ск)]. (1.45)
Здесь Сн и Ск — начальная (на входе в реактор) и конечная концентрации исходного вещества.
В проточных реакторах приближенно полного смешения реагенты смешиваются с продуктами реакции на весьма малой высоте слоя (за малый промежуток времени). Текущая концентрация исходного вещества постоянна почти по всей высоте слоя и равна конечной Ск (рис. 1.11, б). Следовательно, текущая движущая сила [см. уравнение (1.39)] и степень превращения х являются величинами постоянными, т. е. справедливы следующие равенства:
ДС = ДСср = ДСК = const; л: = дгср = л:к = const. (1.46)
Поэтому скорость процесса при приближении к полному перемешиванию можно с достаточной для технических расчетов точностью определить отношениями [ср. с уравнением (1.35) ]:
И = Gn/x; и = Сп/х\ и = дс/т. (1-47)
Кинетические уравнения, аналогичные соотношениям (1.37) и (1.41), будут следующие:
V = Gn/T = kvAСк или и = х/х = k (1 — х). (1-48)
|
|
|
Рис. 1.11. Зависимость выхода продукта (степени превращения) х и концентрации исходного вещества С от времени для процессов: а — идеального вытеснения; б — полного смешения |
А 5
При этом константа скорости окажется иной, чем для идеального вытеснения [ср. с уравнением (1.42)]:
* = - ГТ^Г7- (1-49)
Значения констант скорости процесса в реакторах смешения, как правило, намного больше, чем в реакторах вытеснения, а движущая сила процесса (ср. рис. 1.11, а и 1.11,6) намного меньше. В реальных аппаратах неполного смешения кривые х и С занимают промежуточное положение между кривыми, представленными на рис. 1.11, а и рис. 1.11,6. Развернутое кинетическое уравнение (1.5) пригодно для расчета процесса в реакторах вытеснения и смешения.
Характеристическое уравнение для определения времени контакта газа в реакторе смешения для необратимой реакции л-го порядка по основному веществу А, идущей без изменения объема:
Сд jc С а х |
-- н - н - 1 * (1.50)
KCnA kCnA (1—*)" kC"A~l (І—*)"
Н
Для реакторов с неполным смешением реагентов применяют диффузионную модель, в которой используется характеристическое уравнение идеального вытеснения с добавлением члена, учитывающего перемешивание согласно второму закону Фика:
ДС. д2С,
-kC\. (1.51)
Т э дН2
Здесь £>э — эффективный коэффициент диффузии, сочетающий молекулярное и конвективное (турбулентное) перемешивание; Н — высота слоя катализатора.
По кинетическим уравнениям смешения иногда рассчитывают реакторы кипящего слоя [17, 35]. В отличие от реакторов с одним или несколькими фильтрующими слоями катализатора, для расчета которых применяют уравнения идеального вытеснения, в реакторах с кипящим слоем создаются иные условия для работы катализатора. Прежде всего катализатор для кипящего слоя (КС) должен быть износоустойчивым при перемешивании и трении; его прочность на истирание должна быть на порядок выше, чем в реакторах с неподвижными слоями.
В реакторах с неподвижными слоями гидравлическое сопротивление АР возрастает по экспоненте с уменьшением зерна катализатора, а в реакторах КС оно не зависит от размера зерна при данной высоте слоя. Поэтому в реакторах КС применяют мелкозернистые катализаторы, что дает возможность полностью использовать внутреннюю каталитическую поверхность. В отличие от реакторов с неподвижным слоем в реакторах КС нет местных перегревов в слое и в зерне (вследствие его малых размеров), температура по высоте слоя постоянна, поэтому требования к термостойкости катализатора понижаются. В реакторах с неподвижным слоем, в особенности в трубчатых (см. рис. 1.9, б), для устранения местных перегревов или охлаждений желательно применять катализаторы с повышенной теплопроводностью.
Следует отметить, что кинетические уравнения полного смешения применяют для расчета жидкофазных реакторов с мешалками, используемых в производстве катализаторов.
По температурному режиму процессы и соответствующие им реакторы делят на адиабатические, изотермические и политермические.
Адиабатические процессы происходят без отвода (или подвода) теплоты из слоя катализатора при ламинарном потоке газа, текущего по принципу идеального вытеснения. В результате температура по высоте слоя изменяется по уравнению адиабаты пропорционально тепловому эффекту реакции qv, концентрации Си основного исходного реагента в газовой смеси и степени его превращения х. Уравнение адиабаты в зависимости от известных параметров процесса и задачи расчета выражается различно [9, 19, 35].
Так, для однослойного аппарата, хорошо теплоизолированного снаружи (см. рис. 1.9, а), применяют следующие уравнения (плюс — для экзотермических процессов, минус — для эндотермических):
'и = 'н ± Qp/(0C2), (1-52)
'к ='н ± [<2р/ад] (1-53)
'к ~ tn ±qvCux/c, (1.54)
М = клх. (1.55)
Здесь <н, tK — начальная и конечная температуры на входе газа в слой катализатора и на выходе из него; Qp — общее количество теплоты, фактически выделившееся в результате экзотермической реакции (+) или необходимое для компенсации эндотермических процессов (—); Qp — общее количество теплоты реакции при полном превращении основного исходного вещества (х = 1); Gc — количество реакционной смеси; с — средняя теплоемкость; qv— тепловой эффект реакции на единицу (моль, кг) основного исходного вещества; Си— концентрация основного реагента; At=±(tK—tn)\ Ха — коэффициент адиабатического разогрева газовой смеси, равный тангенсу угла наклона адиабатической линии к оси ординат (рис. 1.12, а и б).
Коэффициент Ла рассчитывают следующим образом:
H~Q'p/(Gct)=4pCjc. (1.56)
В промышленности часто применяют многослойные (многополочные) контактные аппараты [9, 19, 36], а также однослойные аппараты, работающие в циклическом процессе [2, 7, 9, 19]. Для каждого последующего слоя многополочного контактного аппарата, а также для реакторов, работающих в циклических процессах, уравнение адиабаты имеет вид:
TK = tH±K(xK — xH). (1.57)
Здесь хк и хи — степень превращения исходного вещества на выходе из слоя катализатора (конечная) и на входе в данный слой (начальная).
|
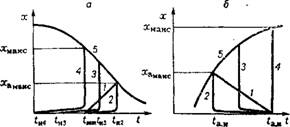
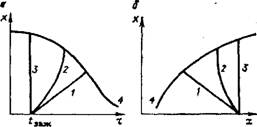
Рис. 1.12. Температурный режим однослойных изотермических реакторов смешения и адиабатических реакторов вытеснения для обратимых реакций: А — экзотермический процесс (/ — адиабата вытеснения; 2, 3, 4 — соответственно изотермы смешения при? н = ?заж. при ?к> *заН(, при tK = ?заж); б — эндотермический процесс (/ — адиабата вытеснения; 2,3,4 — соответственно изотермы смешения без подвода теплоты в слой = ^заж)> с подводом теплоты при частичной компенсации эндотермического эффекта, при полной компенсации эндотермического эффекта подводом теплоты; 5 ■— равновесная кривая = f (t) |
Изотермические процессы протекают при постоянной температуре во всем слое катализатора, т. е. в любой точке t = tK. Более или менее полное приближение к изотерми - чности слоя катализатора может быть достигнуто при: а) непрерывной компенсации теплового эффекта реакции; б) малых тепловых эффектах реакции, концентрации исходного вещества или степени превращения, т. е. при небольшом значении qvCax, когда температура в слое может выравниваться за счет теплопроводности катализатора; в) перемешивании газа и катализатора.
В аппаратах кипящего слоя [17] при перемешивании зерен эффективная теплопроводность слоя катализатора в сотни раз больше, чем неподвижного слоя, и температурный режим близок к изотермическому. Если в кипящем слое нет теплообменных элементов, то при хорошей тепловой изоляции он является одновременно изотермическим и интегрально адиабатическим и tK можно определить по одной из формул (1.52)—(1.57).
Сравнение температурного режима однослойных адиабатических реакторов вытеснения (см. рис. 1.9) и изотермических реакторов смешения (см. рис. 1.10) представлено на рис. 1.12.
Для экзотермических процессов при начальной температуре газа tH = 4аж конечная. температура, соответствующая максимальному (например, равновесному) выходу продукта хмакс, одинакова как при адиабатическом (прямая /), так и при изотермическом (кривая 2) процессах. Однако преимущество изотермического процесса состоит в том, что его средневременная температура больше средневременной температуры адиабатического процесса в т раз:
Т = tK-2,3 lg (tH/tK)/(tH - tv). (1.58)
Следовательно, константа скорости реакции, возрастающая с повышением температуры по экспоненте уравнения Аррениуса (1.4), в изотермических реакторах при значительном тепловом эффекте может быть во много раз выше, чем в адиабатических. При большом значении qvCax следует использовать изотермич - ность для повышения движущей силы процесса и хмакс путем уменьшения начальной температуры ниже температуры зажигания, что допустимо в изотермических реакторах смешения. Теоретически минимальная температура газа, поступающего в реактор смешения, соответствует кривой 4 (см. рис. 1.12) и рассчитывается по уравнению адиабаты:
М = tK — fH = гзаж — tHi = qpCax/c. (1.59)
Практически температура в слое катализатора должна быть выше 4аж и> соответственно газ должен поступать с температурой выше /„4-
Из приведенных рассуждений следует, что разработка технологии приготовления катализаторов с низкой температурой зажигания имеет наибольшее значение для адиабатических процессов в неподвижном слое, а также благоприятно сказывается на выходе продукта изотермических процессов в кипящем слое катализатора.
Для эндотермических процессов при равенстве начальных температур изотермы и адиабаты ta. н изотермический режим (кривая 2, рис. 1.12, б) приводит к снижению средней температуры слоя катализатора, по сравнению с адиабатическим (кривая 1, рис. 1.12, б), и, следовательно, к снижению скорости процесса. Однако, используя высокую эффективную теплопроводность слоя и весьма большие коэффициенты теплоотдачи в изотермических реакторах смешения, следует подводить теплоту непосредственно в слой катализатора и достигать увеличения максимальной степени превращения по сравнению с адиабатой (см. изотермы 3 и 4 на рис. 1.12, б).
Политермические процессы, в которых тепловой эффект реакции частично Компенсируется за счет подвода или отвода теплоты, осуществляются в трубчатых контактных аппаратах, при этом катализатор может быть расположен в трубах (см. рис. 1.9, б) или в межтрубном пространстве [19]. Сравнение температурных режимов на рис. 1.13 показывает, что политермический процесс в одном слое катализатора дает возможность повышать выход по сравнению с адиабатическим. В пределе при полной компенсации теплового эффекта реакции за счет отвода или подвода теплоты политермический процесс переходит в изотермический и достигаются наивысшие степени превращения.
Однако трубчатые аппараты существующих конструкций не позволяют осуществлять режимы, близкие к изотермическим; в них наблюдаются местные перегревы или переохлаждения катализатора, увеличивается гидравлическое сопротивление по сравнению с полочными аппаратами, которые к тому же проще устроены и менее металлоемки. Поэтому в ряде производств [2,
|
Рис. 1.13. Сравнение температурных режимов обратимых реакций в однослойных реакторах для экзотермических (а) и эндотермических ((Г) процессов: 1 — адиабата; 2 — политерма; 3 — изотерма; 4 — равиовеёиая кривая |
19, 37] предпочитают применять катализаторы в многополочных аппаратах с промежуточным теплообменом, которые обеспечивают такой же выход продукта, как и трубчатые, при лучшей сохранности катализатора и меньшем гидравлическом сопротивлении.