Равновесие газ—жидкость в закрытой системе NH3—С02—Н20—CO(NH2)2 с заторможенными реакциями превращения карбамида
Компонентами системы в данном случае являются NHf6, NH2COONH4, СО (NH2)2, Н20, концентрации которых связаны с равновесиями 1, 2, 6 (см. табл. 1.1). Заторможенность равновесий 3, 4, 5 в технике достигается путем выбора соответствующего времени переработки «плава синтеза», недостаточного для развития этих, сравнительно медленных, процессов. Цель переработки — в выделении из «плава синтеза» непревращенного в карбамид карбамата аммония, избыточного аммиака и, частично, воды, что достигается искусственным снижением давления и другими способами.
Состояние системы обычно описывают с помощью констант равновесия, выраженных через активности и летучести [3]. Последние задаются по правилу Льюиса—Рендалла. Что касается жидкой фазы, то при концентрациях компонентов, достигающих десятков моль на литр, длительное время не было возможности использовать без предварительных доказательств какую - либо известную модель реального концентрированного раствора [6]. Поэтому в качестве первого приближения жидкую фазу часто считали идеальным раствором.
Для вычисления констант равновесия в работе [13] использовали данные более двухсот измерений состава жидкой и газовой фаз, полученных при 0,2—49 МПа и 333—493 К. Величины констант коррелировали на ЭВМ по температуре в координатах уравнения Вант-Гоффа, и провели статистический анализ полученных результатов на основе критерия Фишера, задавая довери-
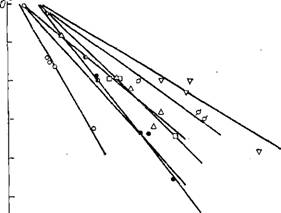
Рис. 1.8. Зависимость lg YNHj—-^«карб» ПРИ P = 1—2,5 іМПа:
О — 336,4 К; О - 346,6 К; А — 359 К; • — 371,5 К; □ — 382 К; а - 393 К
1 V - 401 к.
I тельную вероятность принятой гипотезы 95%. Оказалось, что
I модель идеального раствора непригодна. Чтобы выяснить вопрос о жидкой фазе системы, из массива измерений [13] выбрали
| такие, в^которых газовая фаза практически не содержала С02>
І Н20, а в жидкой сохранялось эквимолярное соотношение карб-
I амида и Н20. Систему в этом случае можно представить как псевдо-
I бинарную смесь: избыточный аммиак — заторможенный «карб-
I амат», в которой первый компонент — летучий «растворитель», а
І второй — нелетучее «растворенное вещество». Затем обычным спо-
| собом вычислили коэффициент активности растворителя — амми-
I ака yNHi (рис. 1.8). В интервале мольных долей «карбамата»
| 0 < Х«карб» <0,6 выполняется следующее правило:
І "gTNH^VCapC, (Ї-40)
І Используя измерения плотности жидкой фазы системы [13]
| и вычисляя среднюю молекулярную массу раствора через молеку-
I лярные массы компонентов, нашли, что мольный объем жидкой
1 фазы в широком интервале изменения Х«карб» описывается урав-
|
|
|
-0,05 |
|
-0,10 |
|
-0,15 |
|
■-0,20 |
|
~0,25 |
|
У зо------ l-.—1-------- 1------ 1------ 1------ 1------ 1------ 1---- • і...... і ' 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 /'('„карб" |
|
M |
|
(1.41) |
|
X |
|
V>K — - Г a^NH3^«nap6) |
|
33 |
|
Более того, вычисляя сжимаемости жидкофазной области системы по данным диаграммы рис. 1.1, определили, что величины 2 Горловский Д. М. и др. |
I нением Бирона:
Д2 и а при одинаковой температуре близко связаны формулой, вытекающей из классической теории регулярных растворов [17]. Итак, отклонения от идеальности жидкой фазы системы описываются закономерностями регулярных растворов, но величины этих отклонений не малы и распространяются на область сверхвысоких концентраций компонентов по сравнению с областью концентраций, при которых применима классическая теория регулярных растворов. Учитывая это обстоятельство, а также то, что доказательства основаны на представлении о сложном компоненте «карбамате», можно назвать жидкую фазу системы псевдорегулярным раствором. Его существование объясняется сильным взаимодействием частиц в растворе (ориентировочное значение избыточного внутреннего давления составляет около 800МПа), приводящим к их значительной ассоциации при сравнительно слабом взаимодействии ассоциатов.
На основе проведенного анализа с использованием представлений термодинамики растворов при высоких давлениях [18] найдено, что наиболее вероятная связь величин констант равновесия процессов 1, 2, 6 (см. табл. 1.1) и параметров состояния должна иметь следующий вид:
Lg Ki (Х{) = А, + А - + f atjXj (1.42)
/
Где і — номер равновесия; /— индекс набора компонентов; atj — независимые от температуры и состава величины.
Корреляцией значений lg Кі на ЭВМ найдены величины Ait Bt, atj (табл. 1.6). По критерию Фишера уравнение (1.42) адекватно описывает весь массив экспериментальных данных с доверительной вероятностью 95% [13, 19]. Уравнение (1.42) используется для расчета равновесных составов сосуществующих жидкой и газовой фаз при рассмотрении различных вопросов статики процесса превращения «плава синтеза» в «плав дистилляции».
|
Таблица 1.6. Величины a,-/, Ah Bit ги щ для констант распределения компонентов между жидкостью и газом в системе NH3—С02—Н20—CO(NH2)2
|
|
Примечание. Здесь г^ — коэффициент множественной корреляции; 0. — среднеквадратичное отклонение. / |