Физико-химическая природа температурного кризиса равновесия реакции синтеза карбамида
Многочисленными опытами показано, что зависимость х*—Т имеет максимум летах в областях существования как одно - i фазной системы—газовой, так и двухфазной — газ—жидкость.
Температура, соответствующая Хщах в системе газ—жидкость, по данным [3] описывается уравнением1:
Тхтах = 273 + 237,5 V 1 - 0.0814L (1.34)
1 Уравнение найдено из условия (дх*/дТ)р, / w = 0 по обобщенному уравнению х* = / (L, W, Р, Т).
|
'піах КР |
Таблица 1.5. Приведенная температура вх = Тх IT
Тг, К
|
2,85 4,00 5,25 |
|
481 469 453 |
|
533 518 503 |
|
0,9050 0,9009 |
|
*тах |
0,9025 | Среднее значение
0,9027
Начальная температура интервала Г0 должна ('совпа - дать с величиной 7Дшах при L~ 4. Действительно, ж « 473 К, а Тх при L =
М "'шах г
= 4 равна 469 К. Таким образом, Ту — такая темпе-
" ' д max
|
1,8 |
|
0,6 0,7 І? Рф |
|
/,0 |
|
1,4 1,6 О |
|
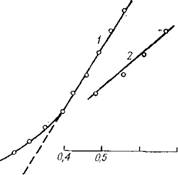
Рис. 1.6. Сравнение равновесных давлений системы NHf—COf (по рис. 1.1) и индивидуальных веществ при одинаковых приведенных температурах кипения: |
|
1,6 |
|
О Vw И п Я Z Q. to 1,2 |
|
1,0 |
|
OA |
|
'Qff |
|
OS |
|
1,2 |
|
"" ^тах Х " Х™ах' Т = Т х' І і Кр л |
|
1 — стандартное вещество вода; 2 ное вещество фосген. |
|
Стандарт- |
|
Понента NH| можно записать: |
Ратура кипения двухфазной системы (NHf—COf), при которой изменяется вариантность системы, что обусловливает термодинамическое подобие ее докритического состояния и критической фазы. Рассмотрим механизм такого подобия. При Т = а при О (синтез карбамида спонтанно заторможен). Следовательно, при закрепленном L в интервале температур и давлений существования псевдоодноком - понентной системы величина х* уменьшается от максимального значения до нуля. Из диаграммы (рис. 1.1) определено, что в интервале Тх — — Ткр и отвечающих ему Рх—Ркр содержится точка Раз, Tai, экспериментально найденная для L = 4 независимо от диаграммы (рис. 1.5, Уші., = 0,8). Это дает основание полагать, что в интервале Тх <С Таз < Г„р и отвечающих ему давлений применим третий закон Вревского [4], который, например, для ком-
|
,2аз lnh, |
|
(1.36) |
|
(dX |
|
ІгХаз 'nh, |
(«к/^іаз^іКн,/^),
(dN*HJdp)
Где Ax — функция от термодинамических потенциалов. Отсюда следует, что
(dp/dT)a3 = (dPjdT) 2аз (1.37)
Nh3
|
Таз — Z-аз НО, 11 |
|
Закрепле- 29 |
Равенство производных для азеотропов и бинарных смесей с закрепленным азеотропным составом жидкой фазы подтверждается данными диаграммы (рис. 1.1) при рсм, отвечающих правилу прямолинейного диаметра, и полученными независимо^экспери
Ментальными значениями Ря
НиеХнн, в свою очередь означает, что действует первый закон Вревского об обогащении газовой фазы труднолетучим компонентом (в данном случае СО?) с ростом температуры [4], т. е.
|
(1.38) |
(,iNlJdT)
>0
,2аз 4nh3
Из (1.38) можно показать, что
|
(1.39) |
|
<Таз<Тк |
|
Хтах |
АГЬаз <0 nh3
Итак, в интервале Т.
Г*
Аз\ [5] кр
Величина л:* уменьшается, а система термодинамически подобна критической фазе вследствие действия третьего закона Вревского. Закрепление
Y2 аз
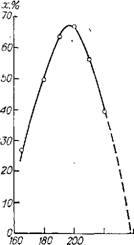
Anh3 в этом интервале температур — это ограничительное условие, которое уравнивает вариантность докритиче - ской двухфазной системы и ее критической фазы. На рис. 1.7 показана зависимость х— Т по данным [15]. При заданном L = 4,41 критические параметры системы таковы: Р1>р « 47 МПа, Ткр = 513 К [10, 11]. Как видно, правая ветвь кривой х—Т легко экстраполируется в х = 0 при Т = Ткр, причем давление в системе близко к критическому
|
220 240 t°C |
|
Рис. 1.7. Зависимость х—t при Р = 40 МПа, L = 4,41. |
По приведенной температуре 6гшах (табл. 1.5) находят Тх = 463 К, что близко к величине (467 К) по рис. 1.7. При заданном L = 4,41 Таз = 498 К, т. е. лежит в интервале Тїшах — — Ткр, а Раз=36 МПа (рис. 1.5) близко к существующему. Таким образом, представления о термодинамическом подобии системы при Т = Тгшах и ее критической фазы, обусловленном законами Вревского, действительно объясняют температурный кризис реакции в двухфазной системе.
Зависимость а^' от температуры и давления (см. рис. 1.2) также легко экстраполируется в значение а^- = 0 при
L к pi
Ткр. Поскольку в данном случае число фаз равно 1, система по сравнению с двухфазной приобретает дополнительную степень свободы и поэтому а— функция двух переменных. Это возможно в том случае, если на состояние равновесия однофазной бинарной системы наложено какое-либо ограничительное условие, например, аналогичное закреплению Для двухфазной
Системы. Выше мы отмечали, что термодинамическое подобие докритической двухфазной системы при Т >• Тх и ее критической фазы требует считать систему псевдооднокомпонентной, о чем и свидетельствует опыт (см. рис. 1.6). Можно предположить, что это условие сохраняется и для пограничной однофазной системы, что снижает число ее степеней свободы с 3 до 2. Для двухфазной системы неравенства (1.38) и (1.39) показывают, что в системе на пути Тх — Таз — Ткр протекает некий процесс, приводящий к снижению х* с ростом Т и обогащению газовой фазы компонентом COf. Условие Хин, = const характеризует стехиометрию этого процесса. Аналогично можно полагать, что и в пограничной газовой фазе также развивается подобный процесс, что снижает вариантность системы на 1 и превращает ее в псевдо - однокомпонентную.
Кризис синтеза карбамида в двухфазной и однофазной системах завершается при параметрах состояния критической фазы, а эта фаза, как указывалось выше, представляет собой бинарный раствор спонтанно заторможенного деструктурированного комплекса в избыточном аммиаке. Возможно, что этот комплекс образуется в критической фазе не скачком, а накапливается при Т >• Тхпах на пути движения параметров системы к параметрам критической фазы. При таком допущении нисходящие ветви кривых на рис. 1.2 и 1.7 характеризуют развитие процесса деструкту - рирования химических связей, из которых можетобразоваться карбамид (например, связей карбаминовой кислоты). Этот процесс конкурирует с реакцией синтеза карбамида и окончательно подавляет ее при критических параметрах. Деструктурирование, так же, как и синтез карбамида, должно быть эндотермическим, причем необходимо, чтобы изменение энтальпии в этом процессе значительно превышало изменение энтальпии при реакции синтеза. Таким образом, можно предполагать, что температурный кризис реакции синтеза карбамида не обязательно определяется фазовым состоянием системы, как это полагали ранее, но может возникать и развиваться на молекулярном уровне.
Изложенная точка зрения позволяет прогнозировать развитие путей значительной интенсификации процесса накопления карбамида в системе. В деструктурированном комплексе, заторможенном в критической фазе, должна быть аккумулирована энергия, соизмеримая с энтальпией образования — распада карбамата аммония («125 кДж/моль). Накопить эту энергию можно, например, путем адиабатического сжатия газовых смесей NHS + + COjS до критических параметров состояния системы (NH?— — СО?)РКр7'Кр. Затем систему быстро выводят из критического состояния в докритическое, в результате чего высвобождается большое количество энергии, необходимой для образования карбамида. «Обвальный» характер правой ветви пространственной кривой на рис. 1.2 позволяет считать, что целевой продукт в результате такой операции может весьма интенсивно образовываться в процессе выпадения конденсированной фазы. Возможно, это радикально изменит представления о масштабе времени реакции синтеза карбамида.
На основе представлений о взаимодействии необратимых процессов в стационарном состоянии [16] проведена полуколичественная оценка. Такая оценка показывает, что скорость реакции способна измениться в таком масштабе, который соизмерим с соотношением скорости конденсации газов в жидкость и скорости массообмена через обновляемую поверхность контакта жидкости и газа. Именно массообмен определяет условия и эффективность синтеза карбамида в современной технологии с продолжительностью протекания процесса в десятки минут. По прогнозной оценке этот масштаб может составлять десятки секунд.