ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

ТЕОРЕТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОНТОГЕНЕЗА

Краткие сведения об онтогенезе, приведенные выше, показы­вают, что он представляет собой необычайно сложную совокуп­ность процессов. В сущности, это самые сложные процессы из всех, с которыми до сих пор встречалась наука. Мы распола­гаем пока знанием ряда поразительных биологических фактов, но лишь в немногих случаях имеем сведения о тех или иных мо­лекулярных событиях в онтогенезе. Построение молекулярной теории онтогенеза, сколько-нибудь полное раскрытие его меха­низмов — дело будущего. Однако имеющиеся данные позволяют уже сегодня провести теоретическое моделирование основных черт онтогенеза и, тем самым, продвинуться на пути познания его сущности. Грубо говоря, следует различать три типа моде­лей — биологические (модель биологического поля Гурвича [116], эпигенетические модели Уоддингтона [107, 115, 117]), ло­гико-математические и физико-химические модели. Общая тен­денция состоит во все большем приближении теоретической мо­дели к реальным физико-химическим процессам, протекающим в онтогенетическом развитии.

Начнем с краткого рассмотрения логико-математических мо­делей. О биологических моделях уже упоминалось в § 9.9.

Д'Арси Томпсон предложил общий аналитический подход к изучению формы у близких видов [125] (ср. [124]). Согласно предложенной гипотезе, если принять форму некоторого орга­низма за эталон и представить ее в некоторой прямоугольной системе координат, то форму другого организма, близкого к эта­лонному, можно рассматривать как результат непрерывной де­формации исходной координатной системы. Однако эта теория трансформаций является сугубо феноменологической, не имеет никаких физических оснований и не раскрывает механизмы мор­фогенеза. Розен предпринял попытку математически обосновать гипотезу Д'Арси Томпсона, исходя из принципа оптимальности [124]. Полученные результаты имеют формальный характер. Не исключено, что они приобретут в дальнейшем серьезное значе­ние при объединении с физико-химическими теориями, но пока теория трансформации остается вне пределов биофизики.

Том предложил абстрактную математическую теорию мор­фогенеза, основанную на весьма общих феноменологических представлениях [126, 127]. Исходная идея Тома — «структурная устойчивость». Некоторый процесс Р структурно устойчив, если небольшое изменение начальных условий переводит его в про­цесс Р', изоморфный процессу Р. Допустим, что в ограниченном пространстве имеется N химических веществ, изменения концен­траций х которых, происходящие вследствие химических реак­ций, описываются кинетическими уравнениями

Xi = fi(x 1, х2, ..., xN), i= 1 N. (9.44)

Эти уравнения определяют в УУ-мерном пространстве векторное поле f с составляющими fi. Изменение системы во времени опи­сывается перемещением представляющей точки X{(t) по неко­торой траектории, определяемой уравнениями (9.44). Так как уравнения нелинейны, в фазовом пространстве возникают син­гулярности, устойчивые или неустойчивые. Том называет цен­тром притяжения системы уравнений (9.44) связное множество точек, образующих предельные траектории. В гиперпространстве система обладает сложной топологией, характеризующей путь ее развития.

Если I — координаты в некоторой области, где определен процесс, то концентрации Xi являются функциями | и времени t. Имеем

1§T = fi(Xj, l,t) + bV2xi, (9.45)

Где последний член описывает диффузию, рассматриваемую То­мом как малое возмущение. Векторное поле fi структурно устой­чиво и определяет динамическое поведение системы. Том рас­сматривает лишь топологию развития в гиперпространстве, ис­ходя из того, что общие черты морфогенеза могут быть поняты без детализированной теории. Это положение, по-видимому, пра­вильно. Феноменология Тома согласуется с представлениями Уоддингтона об эпигенетическом ландшафте и креодах. Истин­ный физический смысл теории Тома сводится к наличию у нели­нейной химической системы множественных сингулярностей, устойчивых и неустойчивых, и к переходам между ними. Для построения теории, доступной экспериментальной проверке, не­обходимы достаточно конкретизированные модели, учитываю­щие реальные черты исследуемого процесса. Модели дифферен - цировки и морфогенеза сходны в методологическом отношении с моделями периодических процессов, рассмотренными в преды­дущей главе.

Эти подходы к рассмотрению систем, обладающих сингуляр- ностями, обобщены Томом [128]. Применения предложенной им «теории катастроф» в биофизике еще не реализованы.

Вольперт предлагает различать процессы, протекающие во времени, и процессы, протекающие в пространстве, — простран­ственную регионализацию, образование структуры, морфогенез. Отметим, что, вообще говоря, такое разделение не имеет осно­ваний, так как пространственное структурирование требует вре­мени, является кинетическим процессом. Можно, однако, рас­сматривать чисто геометрические, топологические проблемы от­дельно от кинетики.

Вольперт справедливо подчеркивает, что в биологической си­стеме программируется путь развития, а не устройство возни­кающего организма. Путь возникновения пространственной структуры — в простом случае осевой, т. е. линейный, — можно формализовать. Проблема состоит в объяснении регуляционного сохранения и восстановления структуры при ее частичном раз­рушении. Так, гидроиды, характеризуемые осевой организацией, обнаруживают способность к регуляции, восстанавливая свою структуру после удаления какой-либо части. Вольперт предло­жил соответствующую топологическую модель, «модель трех­цветного флага», дающую феноменологическое, качественное объяснение регуляции развития, основанное на рассмотрении линейного ряда взаимодействующих элементов, каждой из ко­торых может находиться в нескольких альтернативных состоя­ниях [129, 130].

Мартинец построил теоретическую модель организма, со­стоящего из линейного ряда клеток. Клетка в этом ряду спо­собна делиться лишь в том случае, если концентрация некото­рого вещества в клетке достигает порогового уровня. Скорость изменения этой концентрации зависит от разности концентраций двух других веществ, «морфогенов», причем одно из них может диффундировать из клетки в клетку. Такая модель, являющаяся модификацией модели Тьюринга (см. стр. 418), приводит к не­равномерному распределению материала по клеткам и к спе­цифическому их делению. Модель описывает морфогенез в ус­ловных терминах ([131], см. также [132]).

Общие феноменологические физические подходы к пробле­мам онтогенеза должны, очевидно, основываться на наличии в системе множественных стационарных состояний и переходах между ними. Теория таких переходов применительно к биосин­тетическим процессам развита Лавендой [133]. Основное физиче­ское положение, из которого может исходить теория, состоит в том, что регуляция белкового синтеза, ответственная в конеч­ном счете за онтогенетические процессы, обеспечивается комби­нацией действия структурных генетических факторов и динами­ческих биохимических процессов. Разрывный и необратимый ха­рактер биосинтеза может реализоваться, если на его пути имеется множество различных стационарных режимов.

Будем исходить из модели оперона Жакоба и Моно (см. § 1.6). Соответствующая схема приведена на рис. 9.13. Ген-регу­лятор гр ответствен за синтез белка-репрессора Y, подавляю­щего работу гена-оператора го и, тем самым, структурного гена сг. Сг производит мРНК R, кодирующую синтез фермента Е, превращающего субстрат S в метаболит X, способный обратимо связываться с репрессором Y. Репрессор Y — аллостерический белок, который может существовать в различных конформациях, различающихся по активности связывания с оператором. Ветви а и & на рис. 9.13 представляют активную и неактивную форму

S

I

TOC \o "1-3" \h \z • R »- Е

Го

1 гр | Y |

1 X

Рис. 9.13. Схема биосинтетических процессов. Объяснения в тексте.

Y. Переходы между ними зависят от концентрации метаболита X. Скорость синтеза мРНК лимитируется связыванием метабо­лита репрессором. Процессы транскрипции, трансляции и ме­таболической реакции разделены во времени. Эти положения достаточно обоснованы экспериментально.

Если репрессор Y имеет п активных центров по отношению к X, то степень насыщения репрессора метаболитом, т. е. среднее число молекул метаболита, связанное молекулой Y, равно

J^iLix1

-• - Ч'~0 Ч (9.46)

» ~ д In X

1=0

Где Li = ДоДь • • •, Ki, Кі — константа равновесия реакции

YX,_i + X YXi(

L0 = Ko= 1 (ср. [7], гл. 7).

Так как лимитирующей стадией является именно взаимодей­ствие Y с X, кинетическое уравнение для синтеза мРНК имеет вид

R = r2R. (9.47)

Кроме того,

Ё = R3R — гаЕ, (9.48)

X=r5SE-r6X, (9.49)

Гг — константы скоростей. Для простоты предполагается, что убыль R, Е и X определяется мономолекулярным распадом. Уравнение (9.47) зависит от нелинейной связи Y с X, т. е., от кооперативных свойств Y. Стационарные решения уравнений (9.48) и (9.49) дают

Г> Г4ГЬ X

Г3Г5 s '

Получаем из уравнений (9.46) и (9.47)

Х_ К

(9.50)

Где

Простейшая схема, дающая динамическое кооперативное пове­дение, получается для репрессора с тремя центрами связывания (п = 3). В этом случае стационарные значения концентрации метаболита Х0 удовлетворяют уравнению

Х30 - (ЗА, - U! U) Xi + (L, - 2 L2K) 1з_1Хо - {КЦ - 1) Lz' = 0.

(9.51)'

Согласно теореме Декарта число положительных корней (9.51) не может превышать числа пере­мен знака в этом полиноме. По­этому в рассматриваемом слу­чае возможно не более трех ста­ционарных режимов. Зависи­мость скорости синтеза и рас­пада мРНК от концентрации X представлена на рис. 9.14 [133]. Необходимое условие существо­вания трех стационарных состоя­ний есть ЗКз > К і > 2К2. Раз­личие констант Ки К2, Кз озна­чает кооперативность. Разделив (9.46) на X, получаем эффектив­ную скорость синтеза и скорость распада мРНК (рис. 9.15). Значения Xi и Х2 определяются условием [133]

2= 0 - - sfr) =F { (л - - з^ (£, - 2L2%) }*. (9.52)

Рис. 9.14. Зависимость скорости синтеза (А) и скорости распада (В) мРНК от X.

А. Ь, с — стационарные состояния.

В этих точках сливаются стационарные режимы, соответствую­щие ветвям / и II, Ц и ///. Это — точки ветвления, точки
бифуркации. В точках бифуркации возможны неустойчивые ре­жимы. Лавенда характеризует устойчивость стационарного ре­жима посредством так называемого потенциала скоростей [133]. Анализ показывает, что ветви I и III — устойчивы, ветвь II — неустойчива. Изменения концентрации X приводят в точках би­фуркации к переходам между стабильными ветвями (рис. 9.16).

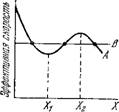
Рис. 9.15. Зависимость эффективной скорости синтеза (Л) и распа­да (В) мРНК от X.

Анализ показывает, что ветвь III является термодинамиче­ской, ветвь I — кинетической.

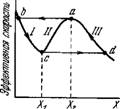
Рис. 9.16. Зависимость эффективной скорости

Синтеза от X. а и с—точки бифуркации, Ь, d—точки, соответ­ствующие стабильным со­стояниям.

В точках бифуркации реализуются пороговые значения кон­центрации, которые наряду с критическими градиентами кон­центраций определяют механизмы, ведущие к контролю и регу­ляции. Пороговые концентрации являются функциональными средствами контроля, зависящими от скоростей химических ре­акций. Критические градиенты концентраций зависят еще от диффузии и могут рассматриваться как структурный контроль­ный механизм, в котором контроль достигается изменением гео­метрии системы.

Таким образом, кооперативность биосинтеза определяет не­линейность, а нелинейность приводит к наличию множественных стационарных состояний и переходов между ними (см. также [132, 134, 135]). Выше рассмотрены аналогии с фазовыми пере­ходами (см. § 8.12).

Регуляторные, триггерные, свойства системы, обладающей множественными стационарными состояниями, можно проде­монстрировать непосредственно с помощью той же модели опе - рона. Жакоб и Моно предложили в качестве триггерной схемы симметричную модель двух оперонов, показанную на рис. 9.17 [136]. Два оперона связаны тем, что метаболит Хь продуцируе­мый первым опероном, связывается репрессором Y2 второго оперона и наоборот. Кинетические уравнения в отсутствие ко-
оперативности у репрессоров Yt и Y2 имеют вид (А, В, Гі — кон­станты) :

= "7гпг7? г

В + е2

/?2

А

- R2R2,

В + Е, Ei=r-sRi — гаЕ\, Е2 = г sR2 — г аЕ2.

В стационарных условиях Rь Й2, Ё\, Ё2 = 0 и

Г2г< В + Е1

D _ Лг3 1 „ /1л3 1

(9.53)

Л2г4 В + Е2>

Кривые Е\(Е2) и Е2(Е\) пересекаются лишь в одной точке, и такая система не является триггерной. Однако, если вместо (9.53) рассмотреть, RPf Нелинейную, кооперативную систему уравнений, имеющую в простейшем слу­чае вид

■r2Ru

(9.54)

■ Г 2%2>

В + ЕІ

Еі = глЯі — rtEu

Аг*

Г2г4 В + Е\'

E2 = r tjR2 — г AE2,

То возникают триггерные свойства, подробно исследованные в работе [137] (см. также [90, 138]). Стационарные кривые вы­ражаются формулами

Агз

R2r4 В + Е'1' ' ,2,4

Они показаны на рис. 9.18. Имеются три точки пересечения а, Ь, с, из которых а и с устойчивы, a Ь неустойчива. Следова­тельно, такая система может при малом изменении параметров переключаться из состояния с, в котором преимущественно син­тезируется белок Еь в состояние а, в котором преимущественно синтезируется белок Е2.

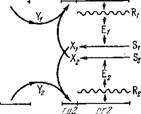
Го1 СП

Rp2

Рис. 9.17. Триггерная схема Жакоба и Моно.

Обозначения те же, что и на рис. 9.13.

Описанные модели имеют принципиальное, а не конкретное значение. Они раскрывают возможный физический смысл про­цесса дифференцировки, определяемого триггерным характе­ром химико-диффузионных явлений. Моделирование конкретных
механизмов дифференцировки требует значительно большей ин­формации о соответствующих химических событиях, чем та, ко­торой мы располагаем сегодня. Детальное исследование онтоге­неза на молекулярном уровне является актуальной задачей науки.

Сходные триггерные модели были эффективно применены к рассмотрению дифференцировки и морфогенеза в работе [139]. При трактовке морфогенеза автор исходит из предположения

О том, что каждый тип клеток секрети - рует специфические химические веще­ства, взаимодействующие друг с другом.

В работе [140] рассматривается дина­мическая неустойчивость реакций и тран­спортных процессов в группах клеток, между которыми имеются коммуника­ции. Показано, что в таких системах возможно возникновение определенной структуры и периодических колебаний. Предложен метод анализа установления нестабильностей в сетях компартментов и в модельных клетках. Сеточная струк­тура влияет на внутриклеточные химиче­ские реакции и межклеточный перенос вещества и, тем самым, на устойчивость стационарных состоя­ний сети. Проведено рассмотрение изменений топологии сети и влияний на ее состояние граничных условий и межклеточных проницаемостей. Эта работа, содержащая новый и ценный фор­мальный аппарат анализа неустойчивостей, находится в об­щем русле исследований нелинейных развивающихся систем, начатых еще Тьюрингом [141] и излагаемых в этой и предыду­щей главах.

В работе [142] эпигенетические представления применены не только к развитию, но и к процессу старения.

В работе Симона [143] была предложена конкретная модель жизненного цикла бактериальной клетки, исходящая из конку­ренции различных ферментов за общий предшественник, а также из лимитирующей роли РНК-полимеразы для скорости тран-^ скрипции.

По-видимому, перспективно теоретическое моделирование; дифференцировки не на основе модели оперона, описывающей? недифференцирующиеся клетки прокариотов, а на основе мої дели транскриптона (см. § 1.7). Эта модель отвечает горазд©- более тонкой и разнообразной регуляции действия генов.

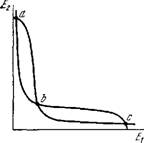
Рис. 9.18. Стационарные кривые для триггерной системы.

Триггерные механизмы показывают определяющую роль ин­формационной программы, ценности, а не количества информа­ции в онтогенезе. В точке бифуркации (точка b на рис. 9.18)
происходит выбор пути развития. Такому выбору отвечает всего лишь 1 бит информации, но избранный путь определяет разви­тие возникающего организма.

Роль триггерных систем в развитии рассмотрена в работе [144]. Информационные аспекты онтогенеза обсуждаются в ра­боте [145].