ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

ТЕОРИЯ ПЕРЕХОДА К БИОЛОГИЧЕСКОЙ ЭВОЛЮЦИИ

В теории Эйгена селекция и эволюция реализуются в си­стеме нуклеиново-белковых гиперциклов. Ответ на вопрос о том, что было ранее — «законодательная» нуклеиновая кислота или «исполнительный» белок — гласит: и то, и другое. Та же схема фигурирует в только что приведенной кинетической модели.

Кун предложил качественную модель происхождения жизни, исходящую из того, что вторая стадия добиологической эволю­ции началась со сравнительно коротких цепей РНК [55]. Опи­шем эту модель.

В «первичном бульоне» происходит синтез и распад нуклео­тидов. Процессы эти грубо периодичны — за фазой образования следует фаза разложения. Чередование фаз определяется сменой высыхания и увлажнения прибрежного раствора. Однако обра­зовавшиеся нуклеотиды полимеризуются, причем в цепи с рав­ной вероятностью входят правая и левая рибоза. Случайное возникновение цепи, содержащей 20 D-рибозных звеньев, имеет вероятность (1/2)20 = Ю-6.

Упорядоченные,- т. е. содержащие лишь один стереоизомер, короткие цепи могут служить матрицами для саморепродукции и они более устойчивы к гидролизу. Тем самым они оказываются способными пережить «фазу вымирания» и реплицироваться дальше. Маловероятные события становятся необходимыми в большой популяции.

Образовавшиеся короткие цепи РНК свертываются в третич­ные структуры. Мы знаем, что молекулы тРНК обладают ком­пактной третичной структурой [56]. Возникает дивергентная фаза эволюции — набор различных третичных структур пра - РНК, различных мутантов. Среди мутантов имеются более устойчивые к гидролизу. Через некоторое число п периодов син­теза и распада сохранятся и размножатся преимущественно эти; мутанты пра-РНК. Условие селекции состоит в том, что следую­щая ошибка репродукции возникает в среднем не ранее чем че­рез п периодов.

Если Z есть число нормальных молекул, приходящихся на один мутант, то вероятность его появления есть 1/Z. В п поко­лениях нет ошибок репродукции. Вероятность появления новой ошибки равна Р, т. е. после 1 /Р поколений каждый потомок му­танта содержит ошибки. Будем считать для простоты, что в 1 \Р поколениях после первого появления выгодного мутанта ошибок нет, а затем они появляются, п есть число поколений, обеспечивающее превращение мутанта в исходную форму. Если 1 /Р <L п, мутант вымирает. При l/P> п вся популяция стано­вится мутантной. Оптимальная вероятность ошибок репродукции дается условием 1/Р = п, т. е. Рп = 1. Пусть число звеньев в цепи РНК N = 50, что примерно соответствует цепи тРНК. При меньших N молекула подвергается гидролизу, при больших N синтез слишком долог. Положим Z — 106 и примем, что ве­роятность выживания выгодного мутанта г вдвое больше ве­роятности выживания исходной цепи, т. е. rn = Z или 2n = 106. Находим п — 20. Условие отбора дает Р ^ 1/20. С другой сто­роны, Р = Nw, где до — вероятность ошибки в одном основании. При N = 50 до должно быть меньше или равно Ю-3. Опыт дает, однако, на порядок большую величину, а именно до ~ Ю-2. Сле­довательно, должен существовать добавочный механизм отбора. Кун предполагает, что этот механизм обеспечивается образова­нием и распадом агрегатов молекул пра-РНК. Возникает почти безошибочная репродукция агрегатов, несмотря на частые ошибки в репродукции отдельных молекул РНК. Молекулы с ошибками агрегатов не образуют. Для агрегатов условие се­лекции достижимо, хотя для отдельных молекул Р = Nw = = 50-Ю-2 = 0,5. С ростом числа репликаций s в фазе синтеза уменьшается доля экземпляров без ошибок и г — фактор пре­имущества — убывает. Возрастание Р = Nws и уменьшение г ведут к обострению условий отбора. Они соблюдаются, если п не слишком велико, т. е. г превышает некоторую критическую величину.

Молекулы РНК в агрегатах лучше защищены от гидролиза. Для того чтобы агрегаты образовывались достаточно быстро, подходящие молекулы РНК должны встретиться за время т, су­щественно меньшее, чем продолжительность фазы вымирания, которую можно считать равной одному дню. Это может быть до­стигнуто путем компартментализации. Если она реализуется в результате попадания молекул пра-РНК в водную среду ме­жду частицами глины, занимающую объем порядка размеров клетки V ~ Ю-13 см3, то время, необходимое для образования агрегата, можно оценить из коэффициента диффузии. По оценке Куна образование линейного агрегата из 20 молекул пра-РНК требует 1 час. Это время может оказаться значительно меньше, если агрегат представляет собой компактную молекулу РНК, служащую для нуклеации агрегата, и присоединенную к ней цепь (пра-мРНК), служащую направляющей для сборки линей­ного агрегата (рис. 9.6), т. е. для объединения пра-тРНК. В этом случае трехмерная диффузия заменяется одномерной.

Таким образом, в принципе возможен устойчивый отбор агре­гатов РНК без участия белков, т. е. без гиперциклов по Эйгену. В модели Куна реализуется ценность информации всей цепи пра-РНК как при возникновении третичной ее структуры, так и при образовании агрегатов.

Предположим далее, что поверхности отобранных линейных агрегатов способны катализировать поликонденсацию активи­рованных аминокислот в пептидные цепи. Это дает селекцион­ные преимущества — агрегаты стабилизуются пептидными молекулами. Ошибки реплика­ции могут оставлять неизменными контакт­ные, каталитические, участки поверхности. Частицы глины (монтмориллонита) также ка­тализируют образование полипептидов [57].

Здесь возникает поворотный пункт — си­стемы образуют полипептидные оболочки и становятся поэтому независимыми от внеш­него компартмента (см. опыты Фокса по об­разованию протеиноидных микросфер [38]). Линейный агрегат, состоящий из пра-мРНК и пра-тРНК, играет роль пра-рибосомы. Наступает новая конвергентная фаза — си­стема, которая быстрее строит свою обо­лочку, имеет селекционные преимущества. Без образования оболочки были бы невозмож­ны переходы на следующие ступени эво­люции.

Описанная ситуация должна возникать в достаточно больших популяциях пра-РНК.

Пра-рибосомы эволюционируют далее — скорость продукции полипептидов оболочки растет вследствие более точного узна­вания аминокислот контактными участками пра-тРНК.

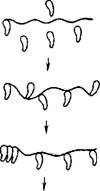
Рис. 9.6. Модель сборки агрегата из молекул пра-РНК по Куну.

Шшг

Возникновение кода начинается предположительно с узна­вания цепью пра-мРНК частиц пра-тРНК. В начале узнается лишь средний нуклеотид триплета, т. е. имеются четыре сорта пра-тРНК - Узнавание означает лучший контакт между молеку­лами и способствует сборке агрегата. Тем самым создается код для четырех аминокислот, но он еще не фиксирован. Форма, случайно синтезирующая особенно полезный полипептид, не мо­жет еще отбираться из-за частых ошибок репликации. Но если полипептид случайно оказывается РНК-репликазой, то вероят­ность ошибки может понизиться по оценке Куна с 10~2 до 10~3. Такая система имеет автокаталитические свойства и получает селекционные преимущества — увеличенный фактор преимуще­ства при размножении г. Информация, заложенная в специфи­ческой последовательности аминокислот, консервируется, и фик­
сируется код для четырех аминокислот или, что более суще­ственно, для четырех групп аминокислот. Дивергентная фаза эволюции переходит при этом в конвергентную. Происходит се­лекция систем, синтезирующих полипептиды с избранной после­довательностью аминокислотных остатков.

Далее постепенно образуются ферменты — аминоацил-синте - тазы для четырех пра-тРНК, что повышает специфичность свя­зывания аминокислот. Как только вероятность ошибки стано­вится меньше критического значения, дальнейшая эволюция происходит с необходимостью. Очевидно, что опасны ошибки в среднем нуклеотиде антикодона. Но после того, как возникла форма, способная к ферментативной репликации с малым чис­лом ошибок, ошибка в антикодоне перестает быть суще­ственной. Каждый индивидуум с такой ошибкой синтезирует неправильный поліпептид и в дальнейшей эволюции не уча­ствует.

Таким образом, должен реализоваться переход к системе, служащей новым целям. Аппарат синтеза неспецифических по­липептидов, образующих оболочку, улучшается и приводит к си­стемам с полипептидами, обладающими определенными после­довательностями остатков. Это означает новые возможности химического поведения. На той же стадии фиксируется хираль - ность аминокислот. В сущности, создается примитивный орга­низм — пра-клетка.

Последующий отбор означает выживание систем с наилуч­шими ферментами. Уменьшается вероятность синтеза «бессмыс­ленных» белков. На этом этапе начинает играть роль первый нуклеотид антикодона. Однако эволюции мешает образование комплементарных нитей РНК, не участвующих в синтезе бел­ков. Рано или поздно случайно возникает белок, катализирую­щий образование ДНК на матрице РНК, что ускоряет размно­жение. Таким образом, предполагается возникновение РНК-за­висимой ДНК-полимеразы. В дальнейшем, после включения ДНК в генетический аппарат, этот фермент более не нужен, но должна функционировать транскриптаза. Цепи ДНК объеди­няются посредством лигаз, создается геном. Сосредоточение всего информационного плана в ДНК дает селекционные пре­имущества, так как уменьшаются нарушения синтеза из-за по­тери тех или иных мРНК и облегчается решение проблем взаи­мосвязи в структуре системы. Репликация ДНК обеспечивает умножение матрицы и, следовательно, добавочное селекционное преимущество.

В результате перечисленных событий возникает «машина», в которой инструктированные белки «подогнаны друг к другу», как колесики в часовом механизме. Практически каждая ошиб­ка останавливает работу всей системы.

Кун предлагает грубую оценку времени, необходимого для инструктирования 103 белков, что соответствует содержанию белков в одной бактериальной клетке.

Заметные селекционные преимущества возникают лишь в тех случаях, когда у вновь инструктируемых белков по крайней мере v мест занято надлежащими остатками. Соответственно 3v кодонов должны располагаться правильно (вырождение кода уменьшает это число). Вероятность найти определенное основа­ние в 3v местах есть (г/4)3v. Следовательно, предельное допусти­мое число мутаций — одна мутация на Z = 43v особей. Фактор преимущества г находится из условия п = In Zjln г. Если уже имеется репликационная система, работающая с оптимальной частотой ошибок, то

П=\/Р = 1/wN И w=l/Nn = (l/N)\nr/\nZ.

Примем, что каждый добавочный белок дает селекционные пре­имущества, в частности, повышает шансы на выживание при­мерно на 20% (г = 1,2). Величина г должна сильно возрастать с v. Допустим, что это возрастание экспоненциально, т. е. г — = exp(v/a). Если при v = 300 г = 1, 2, то а = 500; тогда при v = 5 г =1,01. Примем v = 5, N = 103, что соответствует белку из 300 аминокислотных остатков. Следовательно,

Z = 413« 109, « = 1п 109/1п 1,01 « І03, да» 10~6.

Инструктирование всего белка есть процесс оптимизации. Он требует, чтобы сменилось

Q= N/(3vw)

Поколений (принято, что за N/(3v) последовательных шагов Ин­структируется v аминокислот, 1 /да— число поколений, соответ­ствующее одной ошибке в каждом кодоне). Находим q ~ 108 поколений. За это число поколений ДНК удлиняется на 10s нуклеотидов. Число поколений, нужных для инструктирования 103 белков, равно

Q= Ю3<7~ 1011.

Если новое поколение возникает каждые 20 мин, то время, тре­буемое для эволюции до уровня сложности бактериальной клетки, равно по порядку величины 106 — 107 лет, если на одно поколение нужны сутки, то оно составляет 108— 109 лет. Вели­чина Q слабо зависит от г. Эволюция идет тем быстрее, чем больше популяция, т. е. число Z.

Таким образом, согласно оценкам Куна, эволюция вполне могла осуществиться за время, протекшее с эпохи возникнове­ния жизни на Земле.

Дальнейшая эволюция — возникновение многоклеточных ор­ганизмов из одноклеточных и возникновение всего многообразия видов — связана с возможностью слияния систем с различными белками. Можно привести соображения в пользу того, что это требовало меньшего времени, чем создание первых клеток (см. ниже). Дальнейшее обсуждение проблем, рассмотренных в из­ложенной работе Куна, приведено в следующем параграфе. В работе [58] выполнены расчеты, иллюстрирующие описанную модель эволюции.

Чернавский и Чернавская предложили несколько отличную модель [59] (подробное изложение см. в [90]). В этой работе проведен строгий анализ основных положений теории и развита математическая теория самоорганизации макромолекул, хими­ческой и биологической эволюции, основанная на анализе устой­чивости возникающих состояний системы. В расчетах исполь­зуется метод фазовых портретов. Важным моментом этой теории является предположение об антагонистических взаимодействиях между равноправными объектами, описываемых уравнением

Xi = axt — b 2 ХіХ,, (9.37)

ІФі

Где a, b > 0. Наличие антагонистических взаимодействий озна­чает нелинейность, которая может вести к эволюции. Анализ уравнений типа (9.37) приводится ниже.