Вечный двигатель

Механические ррш

Все механические ррш средневековья (и многие более поздних времен) основаны на одной и той же идее, иду­щей от д'Оннекура: создании постоянного неравновесия сил тяжести на колесе или другом постоянно движущемся под их действием устройстве. Это неравновесие должно вращать колесо двигателя, а от него приводить в действие машину, выполняющую полезную работу.

Все такие двигатели можно разделить на две группы, отличающиеся видом груза — рабочего тела, К первой
группе относятся те, в которых используются грузы из твер­дого материала (назовем их условно «твердотельными»), ко второй — те, в которых грузом служат жидкости (назовем их «жидкостными»). Количество разных вариантов ррт в обеих группах огромно. Описывать их здесь нет смысла, так как это уже сделано многими авторами [2.1-2.6].

Мы ограничимся лишь несколькими образцами, на при­мере которых можно проследить их эволюцию и ход дис­куссий о возможности получения работы.

Начнем с твердотель­ных двигателей. Приме­рами могут служить три варианта ррт, разрабо­танные в разное время и в разных местах. Ита­льянский инженер Мари­ано ди Жакопо из Си­ены (недалеко от Фло­ренции) в рукописи, да­тируемой 1438 г., опи­сал двигатель, повторяю­щий по существу идею д'Оннекура, однако здесь дана уже четкая кон­структивная проработка (рис. 1.5). Грузы, предста­вляющие собой толстые прямоугольные пластины,

Гуг откидываться только в одну сторону. Число их нечетно; поэтому слева

Копо

При любом положении колеса всегда будет больше пластин, чем справа (в данном случае 6 против 5). Это и должно вы­звать непрерывное вращение колеса в направлении против часовой стрелки.

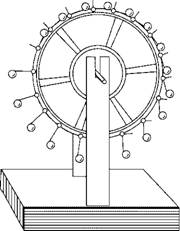
Англичанин Эдуард Соммерсет, тоже разработавший механический ррт в виде колеса с твердыми грузами и в 1620 г. построивший его, принадлежал, в отличие от своих предшественников, к самым аристократическим кру­гам общества. Он носил титул маркиза Вустерширского и был придворным короля Карла I. Это не мешало ему серьезно заниматься механикой и разными техническими проектами. Эксперимент по созданию двигателя был по­
ставлен с размахом. Мастера изготовили колесо диаметром 14 футов (около 4 м); по его периметру были размещены 14 грузов по 50 фунтов (около 25 кг) каждый. Испытание машины в лондонском Тауэре прошло с блеском и вызвало восторг у присутствующих, среди которых были такие ав­торитеты, как сам король, герцог Ричмондский и герцог Гамильтон, К сожалению, чертежи этого ррт до нас не дошли, так же как и технический отчет об этом испыта­нии; поэтому установть, как оно проходило по существу, нельзя. Известно только, что в дальнейшем маркиз этим двигателем больше не занимался, а перешел к другим про­ектам.

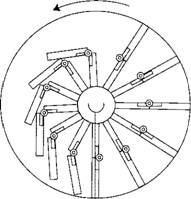
Александре Капра из Кремоны (Италия) описал еще один вариант ррт в виде колеса с грузами. Из рис. 1.6 видно, что дви­гатель представлял собой колесо с 18 расположен­ными по окружности рав­ными грузами. Каждый ры­чаг, на котором закреплен груз, снабжен опорной де­талью, установленной под углом 90° к рычагу. По­этому грузы на левой сто­роне колеса, находящиеся по горизонтали на боль­шем расстоянии от оси, чем справа, должны всегда по­ворачивать его по часовой стрелке и заставлять непре­рывно вращаться.

Заманчивая идея исполь­зовать силу тяжести для создания простого и надежного двигателя оказалась чрезвычайно живучей. Может пока­заться невероятным, но она не потеряла привлекательно­сти для изобретателей и благополучно дожила до XX века. Как пример, можно привести такой «двигатель, исполь­зующий силу тяжести», запатентованный во Франции в 1972 г. неким Ж. Леландэ (патент № 2.102.884, класс F 03, 3/00). Его изобретение не только по идее, но и по конструкции точно повторяет «двигатель» Александре Ка­пра, показанный на рис. 1.6. Разница состоит только в том,
что грузы представляют собой не шары, а прямоугольные бруски, и подвешены не прямо к колесу, а на висящей на нем цепи.

В официальном описании изобретения сказано «двига­тель вырабатывает энергию... снимаемую с его оси без всякого расхода топлива или толчка извне... Автомати­ческая система «цепь-грузы» надета на зубчатое колесо, вращающееся в подшипнике»... Описание заканчивается так. «Энергия, вырабатываемая патентуемым двигателем, может заменить дорогостоящую энергию, вырабатываемую сложными двигателями, использующими дорогое топливо, энергию тепловых и атомных электростанций, гидростан­ций». Из этого описания видно сразу, что изобретение сде­лано в наше просвещенное время, а не в каком-то мрачном средневековье, когда электростанций вообще не было!

Однако для дальнейшего разбора таких «гравитацион­ных двигателей» нужно вернуться к старым временам и вспомнить машины с жидкими грузами.

Жидкостные механические двигатели (с жидкими гру­зами) принципиально ничем не отличаются от описанных твердотельных. Разница состоит только в том, что вместо перемещающихся относительно колеса грузов используется жидкость, переливающаяся при его вращении так, чгобы ее центр тяжести перемещался в нужном направлении.

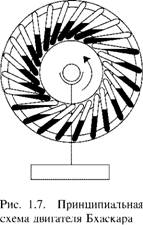
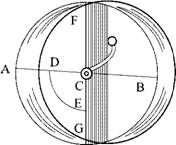
Все такие двигатели в разных видах развивали идею уже упоминавшегося индийца Бхаскара (1150 г.). По описанию можно представить лишь принципиальную схему двигателя [2.6] так, как она показана на рис. 1.7. На окружности ко­леса под определенным углом к его радиусам закреплены на равных расстояниях замкнутые трубки, заполненные тя­желой жидкостью — ртутью. В зависимости от положения колеса жидкость переливается либо во внешнюю, либо во внутреннюю часть каждой трубки, создавая таким образом разницу веса правой и левой частей колеса.

Не вдаваясь в подробности1, Бхаскара пишет: «...на­полненное таким образом колесо, будучи насажено на ось, лежащую на двух неподвижных опорах, непрерывно само по себе вращается».

Историки отмечают, что древнеиндийские ученые, как правило, не прибегали к подробным доказательствам, рассчитывая, по-видимому, на достаточно сообразительного читателя. Они просто давали схему и писали: «Смотри».

Все последующие проекты ме­ханических ррш как с жидкими, так и с твердыми грузами в сущ­ности повторяли ту же идею: со­здать так или иначе постоянный перевес одной стороны колеса над другой и тем заставить его непре­рывно вращаться. Можно было вместо одного колеса использо­вать несколько связанных между собой колес, как в проекте Виль­гельма Шретера (1664 г.); можно было сделать грузы в виде перека­тывающихся шаров или роликов или тяжелого ремня. Все они и множество других проектов опи­саны в литературе [2.3-2.6].

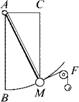
Была даже идея заставить ко­лесо катиться, сделав его в виде барабана, разделенного вертикальной перегородкой (рис. 1.8). По обе ее стороны должны были быть залиты две жидкости разной плотно­сти (например, вода и ртуть). Автор этой идеи Клеменс Септимус был учеником Галилея (правда, ничем не просла­вившимся). Описание этого двигателя помещено в книге известного физика Джиованни Альфонсо Борелли (1608- 1679 гг.), члена Флорентийской академии[3]. Любопытно, что в комментариях Борелли доказывал неработоспособ­ность этого двигателя. Он считал, что нет никаких при­чин, чтобы барабан Септимуса катился; если бы он и сдви­нулся, то достиг бы положения равновесия и остановился. Основанием для такого утверждения служила мысль о том, что сила тяжести, действующая одинаково на все части устройства, не может стать причиной постоянного нару­шения равновесия. Сила тяжести не может производить работу, передаваемую какой-либо машине, которая ее ис­пользует.

Очевидно, что Борелли уже хорошо понимал, что силы тяготения не могут производить работу, если тело нахо­
дится на горизонтальной плоскости и его центр тяжести не опускается.

Средневековая идея применения для создания двигателя сил тяже­сти, которую отвергал еще Борелли, не исчезла со временем; она до­жила до XX в. и была использована в самом передовом направлении техники — для космических полетов. Правда, это произошло в фанта­стическом романе Г. Уэллса «Первые люди на Луне» (1901 г.). Его герой Кэйвор изобрел необычайный материал — «кэйворит», сделанный из «сложного сплава металлов и какого-то нового элемента — кажется, гелия». Этот материал был непроницаем для тяготения. «Какие чу­деса, какой переворот во всем!» —восклицает другой герой книги — Бэдфорд. «Например, для поднятия тяжести, даже самой громадной, до­статочно было бы подложить под нее лист нового вещества и ее можно было бы поднять соломинкой».

Нетрудно представить себе, что самое обыкновенное колесо, даже без хитрых грузов, стало бы само вращаться со страшной скоростью, если бы под одну его половину положить лист «кэйворита». Половина его, сохранившая вес, всегда перетягивала бы другую, ставшую невесо­мой; средневековая идея ррт была бы легко реализована.

Кэйвор и Бэдфорд использовали «кэйворит» для полета на луну. Та­кой же материал под названием «лунит» был применен коротышками — героями известного романа-сказки Н. Носова «Незнайка на луне», чтобы улететь с луны на землю. Но коротышки пошли еще дальше — нашли другой материал — «антилунит», нейтрализовавший действие первого!

Д. Борелли не был пер­вым, кто отвергал уже в то время возможность создания механического ррт, осно­ванного на использовании сил тяжести. Его позиция отражала более общую тен­денцию. Пока изобретатели механических ррт ломали головы над очередными ва­риантами своих машин, по­степенно развивалась меха­ника (и не без их помощи оттачивала свои положения в дискуссиях с ними). Она вырабатывала новые пред­ставления, которые шли дальше античной механики и по­зволяли количественно точно определить результат одно­временного действия на тело нескольких сил. Тем самым новая наука подрывала «под корень» идейную базу меха­нических ррт. Действительно, если выработано четкое
правило, как подсчитать результат действия сил, прилагае­мых к колесу (или колесам) ррш, то всегда легко опреде­лить, будет колесо в равновесии или нет. В первом случае двигатель работать не сможет. Если же, напротив, будет доказано, что неравновесие будет существовать постоянно, то ррш «может жить». Дело, таким образом, сводилось к установлению соответствующего закона механики (точнее, ее раздела — статики).

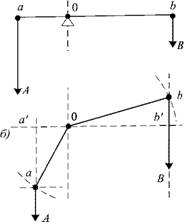
Первый шаг в этом направлении сделал, по-видимому, великий Леонардо да Винчи (1452-1519 гг.). В рукописи 1515 г. он ввел понятие, которое теперь называется в механике «статическим моментом силы». Со вре­мен Архимеда был изве­стен закон, который опре­делял условия равновесия прямого рычага. Он соста­влял содержание VI тео­ремы Архимеда из сочи­нения по механике: «Два соизмеримых груза нахо­дятся в равновесии, если они обратно пропорцио­нальны плечам, на кото­рые эти грузы подвешены». Другими словами (рис. 1.9, а), если силу тяжести (т. е. силу, с которой грузы при­тягиваются к земле) изо­бразить в виде отрезков А и В соответствующих напра­влений и длины, то усло­вие равновесия будет та­ким: А : В = Ob : Оа, или, что то же самое (следует из свойств пропорции), А • Оа = В • Ob.

Таким образом, условие равновесия рычага может быть выражено и так: «Произведения веса каждого груза на дли­ну того плеча рычага, на котором он подвешен, должны быть равны».

При всей его важности закон рычага Архимеда не мог быть использован для анализа равновесия любого колеса механического ррш, работающего с твердыми или жид­
кими грузами. Дело в том, что для такого анализа нужно было уметь определять равновесие и для случая, когда сила веса груза направлена не под прямым углом к рычагу, как у Архимеда, а под любым углом — острым или тупым. Дей­ствительно, стоит посмотреть на рис. 1.3 или 1.6, чтобы увидеть, что сила тяжести направлена под самыми разными углами к соответствующим радиусам колеса. Выделим для примера два груза: один (В) расположен выше оси колеса, а другой (А) ниже (рис. 1.9, б). Как решить задачу в этом, более общем случае?

Леонардо нашел такое решение, он показал его на двух примерах (соответствующие рисунки из его рукописи по­казаны на рис. 1.10). Относящийся к левому рисунку текст предельно ясен: «Пусть AT — ры­чаг, вращающийся во­круг точки А. Груз О подвешен в точке Т. Сила N уравновеши­вает груз О. Проведем линии: АВ перпендику­лярно ВО и АС перпен­дикулярно СТ. Я назы­ваю AT действительным рычагом, АВ и АС — «потенциальным рычагом». Суще­ствует пропорция N : О = А В : АС».

Очевидно, что это соотношение может быть перепи­сано так: О • АВ = N • АС. Другими словами, для рав­новесия ломаного рычага нужно, чтобы произведения сил на соответствующие «потенциальные рычаги» были равны. Эти «потенциальные рычаги» есть не что иное, как про­екции рычага AT на соответствующие оси, перпендикуляр­ные направлению сил, т. е., говоря по-современному, на «плечо силы». Условие равновесия состоит в равенстве статических моментов сил, т. е. произведений сил на про­екции плечей рычага на оси, перпендикулярные направле­нию этих сил.

Аналогичное соотношение было выведено Леонардо для случая, показанного на правом рисунке. Здесь F : М = АС : AM. Из него тоже вытекает равенство моментов сил: F • AM = М • АС.

Вернемся к примеру, показанному на рис. 1.9, б. Поль­зуясь условием Леонардо, получаем, что равновесие насту­
пит при соблюдении равенства А • а/О = В • ЫО. Для проверки возможностей любого механического ррш нужно сложить все моменты сил (грузов), расположенных справа от оси О, и то же проделать с грузами, расположенными слева. Первые стремятся повернуть колесо по часовой стрелке, вторые — против. Если общая сумма моментов будет равна нулю (так как их знаки противоположны), то колесо не двинется — наступит равновесие.

Таким путем легко показать, что несмотря на все ухищ­рения, сумма моментов сил у всех механических ррш равна нулю. Леонардо понимал это очень четко. Стоит только вспомнить слова из одной его записи по поводу ррш: «Ис­катели вечного движения, какое количество пустейших за­мыслов пустили вы в мир!»

К сожалению, записи Леонардо остались неизвестными ни его современникам, ни ближайшим потомкам. Только с конца XVIII в. началась планомерная расшифровка его тетрадей.

Задачу создания теории, позволяющей научно подойти к анализу механических ррш и ответить на вопрос об их ра­ботоспособности, решил англичанин Джон Уилкинс, епис­коп Честерский (1599-1658 гг.). Его работа была вполне самостоятельна, поскольку ему не были известны резуль­таты Леонардо, полученные более чем на столетие раньше.

Уилкинс опубликовал свою теорию в книге «Матема­тическая магия», вышедшей в 1648 г. на английском (а не на латинском!) языке. В ней совершенно четко говорится о статическом моменте силы — одном из основополагающих понятий статики.

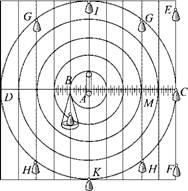
Изобретатели механических ррш с грузами, основыва­ясь на известном архимедовом законе рычага, полагали, что чем дальше от центра колеса находится груз, тем он сильнее должен поворачивать колесо. Это правило дей­ствительно верно, но только для горизонтального рычага (именно его рассматривал Архимед). Распространять его на все грузы, независимо от их расположения на окружности колеса, неверно. Уилкинс наглядно это показал. Ход его мыслей легко проследить с помощью рис. 1.11, на котором изображена схема колеса с центром в точке А. Горизон­тальный диаметр DC колеса разделен на 10 равных частей, и через соответствующие точки проведены концентриче­ские окружности с центром в точке А. В разных точках окружностей расположены одинаковые по весу грузы, ха­рактер движения которых надо определить. Если грузы
расположены на горизонтальном диаметре, задача реша­ется просто — на основе правила Архимеда. Например,

Груз в 1 фунт в точке С уравновесит 5 фунтов в В, поскольку плечо АС в 5 раз длиннее плеча А В. Уилкинс отмечает, что это соотношение останется в силе, даже если груз будет в точке Е или F, лишь бы они были на той же вер­тикали, что и С. Другая ситуация возникнет, ко­гда грузы будут находиться не на горизонтальном диа­метре, а выше или ниже его, как, например, грузы G, Н или /, К. Уил­кинс правильно понял, что в этом случае сила, с кото­рой они будут стремиться вращать колесо в соответ­ствующую сторону, будет другой. Очевидно, что грузы /, К вообще в этом отно­шении бесполезны, а грузы G и Н потеряют часть своей силы. Чтобы определить действие каждого из них, нужно умножить его вес на длину того отрезка горизонтального диаметра, который находится между точкой А и верти­кальной линией, проходящей через точку привеса груза. Для грузов G или Н это будет точка М.

Таким образом, Уилкинс показал, что воздействие груза, вращающего колесо, определяется произведением силы (в данном случае — веса груза) на плечо (в данном случае — отрезок горизонтального радиуса до пересечения с верти­калью, проходящей через центр груза). Равенство всех та­ких произведений — моментов сил, действующих на ко­лесо, обусловит его равновесие; неравенство — постоян­ное вращение. Остается только показать, что в любом из механических ррт такое равенство всегда соблюдается, и невозможность их действия доказана.

Уилкинс, правда, не ввел термина «момент силы», но от этого дело не меняется: важнейший закон статики был установлен. Работа Уилкинса помогла в дальнейшем меха­никам выдвинуть положения, которые вплотную подвели
их к закону сохранения энергии и окончательно похоро­нили идею ррш-1. Но до этого было еще далеко.

Однако тучи над ррш сгу­щались не только со стороны теории. Неудачи с практиче­ской реализацией самых раз­ных моделей тоже постепенно делали свое дело. Поэтому у некоторых (правда, очень немногих) изобретателей по­являлось разочарование в идее ррш. Нашелся и достаточно мужественный человек, чтобы признаться не только самому себе, но и другим в бесполез­ности своей многолетней ра­боты над такими машинами. Это был немец Иоганн Ио­ахим Бехер, который создал довольно сложный «физико - механический» ррш для при­вода часового механизма. Идея двигателя та же, что и дру­гих, описанных ранее, — дви­жение перекатывающихся ша­ров — грузов, которые должны были приводить в движение систему взаимосвязанных ше­стерен и рычагов. Работа шла столь успешно, что курфюрст г. Майнца приказал воздвиг­нуть специальную каменную башню для размещения часов с двигателем Бехера. (Было это в 1660 г., почти в то же время, когда вышла книга Уилкинса.) Однако в дальней­шем это устройство не оправдало возлагавшихся на него надежд.

Бехер подвел итоги своей работы такими словами: «Де­сять лет я занимался этим безумием, потеряв кучу времени, денег и погубив свое доброе имя и славную репутацию — все это лишь для того, чтобы сегодня с полной убежден­ностью сказать: вечное движение — неосуществимо». Это признание осталось, к сожалению, неизвестным многочи­сленным изобретателям ррш.

Вопрос о несостоятельности механических ррт с коле­сами и грузами был теоретически решен, хотя еще долгое время его понимание не стало общим достоянием. Но ме­тод Уилкинса не мог непосредственно помочь при спорах о другом варианте механического ррт, например таком, который показан на рис. 1.12, где ремень (или цепь с гру­зами) с одной стороны тяжелее, чем с другой. Должна ли «работать» эта разница в весе или нет?

Теорию, которая позволила решить этот вопрос, разра­ботал еще раньше замечательный голландский математик, механик и инженер Симон Стевин (1548-1620 гг.). Эта те­ория относится к равновесию тел, находящихся на наклон­ной плоскости, но выводы из нее имеют и более общее значение. Самое интересное в ходе рассуждений Стевина то, что он даже не считает необходимым доказывать невоз­можность создания ррт; он считает это истиной, не требу­ющей доказательства, — аксиомой. Такую четкую позицию занимал до Стевина только Леонардо да Винчи.

Рисунок, относящийся к теории равновесия тел на на­клонной плоскости, Стевин счел настолько важным, что вынес его на титульную страницу своего трактата «О равно­весии тел», изданного в Лейдене (1586 г.). На рисунке Сте­вина (он воспроизведен на рис. 1.13) показана трехгранная призма, грани которой имеют разную ширину. Самая ши­рокая грань установлена горизонтально, ниже других. Две другие, наклонные, сделаны так, что правая имеет ширину вдвое меньшую, чем левая. На призму накинута замкну­тая цепь с 14 тяжелыми одинаковыми шарами. Рассматри­вая равновесие этой цепи, можно видеть (если исключить нижние восемь шаров, которые, очевидно, уравновешены), что на меньшей грани находятся два шара, а на большей — четыре. «Будет ли цепь находиться в равновесии?» — спра­шивает Стевин. Если это так, то происходит чудо. Четыре шара уравновешиваются двумя!

«Не будь это так, — пишет он, — ряд шаров должен был бы (придя в движение) занять то же положение, что и раньше. По той же причине восемь левых шаров должны были бы, как более тяжелые, чем шесть правых, опускаться вниз, а шесть — подниматься вверх, так что шары совер­шали бы непрерывное и вечное движение».

Таким образом, возникает вопрос, ответ на который вы­несен на надпись рисунка, помещенного на титульном ли­сте: «Чудо не есть чудо» (на фламандском языке).

Рис. 1.13. Рисунок с титульной страницы трактата С. Стевина «О рав­новесии тел»

Стевин, исходя из невозможности вечного движения, утверждает, что никакого чуда нет и два шара совершенно «законно» уравновешивают четыре. Он выводит теорему: «Тело на наклонной плоскости удерживается в равновесии силой, которая действует в направлении наклонной плос­кости и во столько меньше его веса, во сколько длина наклонной плоскости больше высоты ее».

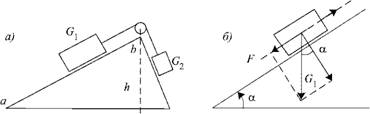
Если взять два груза G и G2 (рис. 1.14, а), то условие их равновесия для данных задачи Стевина запишется так:

G ab 1 ~G~2 = b~c = 2'

Четыре шара весят как раз вдвое больше, чем два.

Пользуясь современной терминологией, можно выра­зить эту теорему в более удобной форме (рис. 1.14, б) сила

Ft удерживающая груз на наклонной плоскости и равная по значению противоположно направленной силе F, стре­мящейся его сдвинуть, определяется (если пренебречь тре­нием) произведением его веса G на синус угла а наклона плоскости к горизонтали:

F = Gsin а.

Если плоскость вертикальна, то а = 90° и since = 1, тогда F = G; если плоскость горизонтальна, то а = 0 и

F = 0.

Стевин уверенно, опираясь на бесчисленные практиче­ские данные, вывел один из важнейших законов статики. Применяя этот закон к проектам ррт вроде показанного на рис. 1.12 и аналогичных ему, легко видеть, что вес на­клонных частей тяжелого ремня (или грузов), висящих по диагонали, нельзя считать равным силе, с которой они по­ворачивают колеса двигателей. Нужно учитывать, что эта сила тем меньше, чем больше отклоняется ремень (или цепь с грузами) от вертикали. Если в каждом конкретном случае произвести соответствующий расчет, то выяснится, что силы, действующие с обеих сторон на колесо (или ко­леса) двигателя, будут неизбежно в точности одинаковы.

Таким образом, Уилкинс и Стевин создали научную базу, позволяющую показать нереализуемость любого ме­ханического ррт. Тем не менее отсутствие общей теории, показывающей неосуществимость любого ррт, оставляло возможности поиска как новых решений ррт, так и обо­снований возможности его существования.

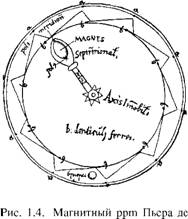
Это особенно чувствуется при ознакомлении с магнит­ными ррт. Наука о магнитах, в отличие от механики, была в самом зачаточном состоянии; поэтому и дискуссия вокруг них велась, главным образом, в общефилософском плане.