Технологическое оборудование машиностроительных производств
ОБЩАЯ МЕТОДИКА НАЛАДКИ МЕТАЛЛООБРАБАТЫВАЮЩИХ СТАНКОВ
Уравнение кинематического баланса. Для большинства металлообрабатывающих станков независимо от их сложности методика наладки одинакова. Она заключается в сообщении исполнительным органам станка согласованных друг с другом движений для изготовления деталей.
Процесс наладки станка требует расчета передаточных отношений органа, наладки скоростей для получения заданной частоты вращения шпинделя и передаточных отношений органов наладки цепей для осуществления необходимых подач (подачи).
Для этих целей намечают расчетные кинематические цепи, составляют расчетные перемещения конечных звеньев этих цепей и уравнения кинематического баланса, из которых выводят формулы наладки цепей.
Уравнением кинематического баланса называют уравнение, связывающее расчетные перемещения конечных звеньев кинематической цепи. Это уравнение служит основой для определения передаточных отношений органа наладки. Конечные звенья могут иметь как вращательное, так и прямолинейное движение. Если оба конечных звена вращаются, то расчетные перемещения этих звеньев условно записывают следующим образом: лнмин-1 -» лкмин-1. Стрелка в этой записи заменяет слово «соответствует». По этим расчетным перемещениям составляют уравнения кинематического баланса данных кинематических цепей: пн • /пост • /х = Якмин'1, где пк — частота вращения в минуту конечного звена органа наладки; пн — частота вращения в минуту начального звена органа наладки; /пост — постоянное передаточное отношение органа наладки; /х — искомое передаточное отношение органа наладки.
Решая уравнения кинематического баланса относительно /х, получим формулы наладки рассматриваемых кинематических цепей.
Если одно из конечных звеньев в кинематической цепи имеет вращательное движение, а другое — прямолинейное, то при подаче, выраженной в миллиметрах на один оборот начального звена, расчетные перемещения можно записать: 1 оборот начального звена -» Suu продольного перемещения конечного звена. Уравнение кинематического баланса будет иметь вид: 1 оборот начального звена іпосг • /х • 1 = =5, где S — перемещение кинематической пары, преобразующей вращательное движение в прямолинейное (например, перемещение гайки за один оборот винта), мм; 1 = Z • Рь (здесь Z— число заходов винта; Рв — шаг винта, мм).
При наладке станков в общем случае необходимо:
1. По технологическому процессу изготовления детали установить характер движений в станке и их взаимосвязь;
2. Определить все кинематические цепи, по которым будет осуществляться необходимое для этого движение;
|
|
3. Составить соответствующие уравнения кинематических цепей, связывающих попарно рабочие органы станка;
4. По полученным передаточным отношениям вычислить и подобрать сменные зубчатые колеса и т. п.
При составлении уравнения кинематической цепи безразлично, в каком порядке рассматривается данная кинематическая цепь — от первого элемента ее (считая в направлении передачи движения) к последнему звену или наоборот, от последнего звена к первому.
У некоторых металлообрабатывающих станков для наладки кинематических цепей применяют устройства, называемые «гитары». В основном металлорежущих станках встречаются двухпарные гитары, лишь в редких случаях, когда необходимы особенно малые передаточные отношения или требуется особенно высокая точность подбора этих отношений, используют трехпарную гитару.
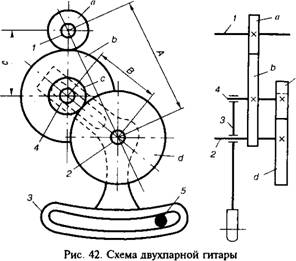
На рис. 42 показана схема двухпарной гитары. Расстояние А между ведущим 1 (колеса а) и ведомым 2 (колеса Ь) валами неизменно. На ведомом валу свободно посажен «приклон» 3 гитары. В приклоне имеются радиальный и дуговой пазы. В радиальном пазу закреплена ось 4 колес «Ь» и «с». Перемещая ось вдоль паза, можно менять расстояние В между колесами «с» и «d». Дуговой паз в приклоне позволяет изменять расстояние между колесами «а» и «Ъ» при повороте приклона на валу 2. В требуемом положении приклон закрепляют болтом 5. Чтобы подобранные зубчатые колеса могли переместиться на гитаре и не упирались во втулки валиков зубчатых колес, необходимо соблюдать следующие условия зацепляемости: а = Ъ> с + 15...20 мм; с+*/>/>+ 15...22 мм. Необходимо также, чтобы 0,2 </<2,8. Суммы 64 чисел сопряженных колес не должны превышать допустимого значения, определяемого конструкцией и размерами места, отведенного для размещения гитары на станке. Нормальные комплекты сменных зубчатых колес приведены в табл. 5. Существует несколько способов подбора чисел зубьев сменных зубчатых колес.
Способ разложения на простые множители применяют в том случае, если на них можно разложить числитель и знаменатель передаточного отношения, полученного по уравнению наладки. Произведя разложение, сокращают дробь или вводят дополнительные множители, комбинируя их так, чтобы получить выражение дроби через числа зубьев, имеющихся в комплекте сменных колес.
Способ замены часто встречающихся чисел приближенными дробями заключается в том, что часто встречающиеся числа я; 25,4; я/25,4 и 25,4я заменяют приближенными величинами, дающими возможность с достаточной точностью получить передаточные отношения. Этот метод применяют на токарно-винторезных станках при необходимости нарезания модульной или питчевой резьбы, а также при нарезании дюймовой резьбы при отсутствии в наборе колеса с числом зубьев Z= 127.
Логарифмический способ основан на том, что находят логарифм передаточного отношения (если передаточное отношение имеет вид неправильной дроби), берут логарифм величины обратной передаточному отношению, и по соответствующей таблице (таблица В. А. Шишкова) определяют числа зубьев сменных зубчатых колес. Этот способ основан на принципе логарифмирования передаточного отношения и дает зубчатые колеса, кратные пяти, с весьма малой ошибкой. Передаточное отношение зубчатых колес гитары / = (а/Ь) • (c/d) после логарифмирования имеет вид: lg/ = lg ас — lg bd (табл. 5).
Метод подбора чисел зубьев на логарифмической линейке. Край движка логарифмической линейки устанавливают против числа, соответствующего передаточному отношению; передвигая визир, находят риски, совпадающие на движке и на линейке. Риски должны соответствовать целым числам, которые дают при делении значение передаточного отношения. Затем подбирают числа зубьев сменных зубчатых колес. Этот способ подбора колес при нарезании резьб применять, как правило, нельзя, так как его точность обычно невысока.
Подбор чисел зубьев по таблицам М. В. Сандакова. Очень часто передаточные отношения содержат дробные числа в числителе и знаменателе или множители, не кратные набору колес. В этом случае удобно подбирать числа зубьев зубчатых колес по таблицам М. В. Сандакова, содержащим до 100 ООО передаточных отношений. Заданное передаточное отношение в виде простой правильной дроби, неудобной для преобразования, нужно прежде всего превратить в десятичную дробь с шестью знаками после запятой. Если дробь неправильная, то необходимо разделить ее знаменатель на числитель, чтобы получить десятичную дробь меньше единицы. После этого в таблице находят десятичную дробь, равную полученной, или ближайшую к ней, а рядом — соответствующую ей простую дробь. Получив простую дробь, числа зубьев сменных колес подбирают обычным способом: например, / = =223/137, откуда 1// = 137/223 = 0,614346. Из таблицы М. В. Сандакова имеем значение 0,614346, равное 728/1185. Ввиду того, что у передаточного отношения перед обращением его в десятичную дробь числитель и знаменатель поменяли местами, у приближенного числа делают то же самое. Тогда і = 223/137 = 1185/728 = (3 х 5 х 79)/(2 х 2 х 2 х 7 х х13) = (60/56) х (79/52). Подобранные колеса имеются в наборе для затыловочных станков.