ЕЛЕМЕНТИ, НА ЯКІ ДІЮТЬ ОСЬОВІ СИЛИ ТА ЗГИНАЛЬНІ МОМЕНТИ
|
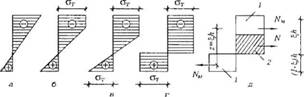
Рис. 3.8. Епюри напружень від одночасної дії осьових сил і згинальних моментів: а—г — послідовні етапи утворення шарніра пластичності; д — розрахункова схема. |
Розглядаючи одночасну дію на стержень осьової стискальної сили і згинального моменту, скористаємося принципом незалежності їх дії. Від обох навантажень у перерізах елемента виникатимуть нормальні напруження. Епюра напружень від дії
Розрахункова схема для обчислення несучої здатності у цьому випадку зображена на рис. 3.8, д. Згинальний момент М, який діє у перерізі, можна замінити парою сил NM, прикладених з плечем 2. Ці сили є рівнодійними силами частин 1 епюри напружень.
Рівнодійна частини епюри 2 (заштрихована) відповідає нормальній силі N. Розглянемо прямокутний переріз розмірами bx h. Висота частини перерізу 1 становить (] — £,) h, де — відносна висота стисненої зони перерізу.
Таким чином,
N„ = Ь-(1 - Q ■ h ■ а,. = b - h-(1 - І;)-аг, М = NM ■ z = Ь ■ h ■ (1 - £) • а.,. • • h = = b - h2 ■ £,(1 - l)a. r, N = Ъ (1 - 2І;) - h ■ стт = b ■ h ■ (1 - • ст.,,. Позначивши
|
И, |
|
W„ |
N M
= v,
A„ ■ стт
' n, pl ^T
|
N |
|
= 1 |
|
І,1 = |
|
А„ст. г М W„ р1 • ст. г |
|
B ■ h" ■ ст.. |
Де An ■ Gr — осьове зусилля, при якому досягаються напруження текучості за відсутності згинальних моментів; W„ pi - о.,. — те ж, згинальний момент за відсутності осьової сили. Обчислимо
B-h-(l - 2Е,) - ст.,.
(3.43)
B - h - стт
= 4Ј(1
4 (3.44)
Де W„ p| = b ■ h2 — пластичний момент опору. Визначаємо t, з (3.43):
R v + 1
Далі, підставляючи в (3.44), отримуємо гг + р = 1,
Або
М
(3.45)
-А-п" ст..
Замінюючи о.,, на значення розрахункового опору металу, приймаючи Wn р1 = ct ■ W„ і вводячи коефіцієнт умов роботи конструкції, отримуємо умову міцності для прямокутного перерізу:
М
(3.46)
Ап ■ Rv ■ Yr
С, • Wn - Ry-Ус
/
Відповідно до форми перерізу показник степеня при першому доданку матиме інші значення.
У загальному вигляді норми рекомендують таку форму запису умови міцності позацентро - во-стиснених і стиснено-згинаних елементів при допущенні пластичних деформацій:
М
<1, (3.47)
An -Ry - Yc
С, ■ Wn ■ Ry ■ Yc
Де n — коефіцієнт, що залежить від форми перерізу.
Наприклад, для двотаврових симетричних перерізів, замкнутих прямокутних профілів і труб його значення становитиме 1,5.
|
N |
|
^х * wm Ry Yc |
При наявності згинальних моментів у двох площинах умова міцності матиме вигляд
М,
Ry Yc
< 1.
(3.48)
С • W • R ■ v
У v* yn 1С
Елементи зі сталей підвищеної і високої міцності, межа текучості яких перевищує 580 МПа, через нижчі пластичні якості матеріалу необхідно розраховувати лише в пружній стадії (3.42). Елементи з м'яких, пластичних сталей, при стт < 580 МПа розраховують у пружно-пластичній стадії за формулами (3.47), (3.48). Це стосується і характеру навантажень. У випадку навантажень, які сприяють крихкому руйнуванню (динамічний характер навантаження, наявність великих пере - різувальних сил і > 0,5Rs тощо), необхідно користуватися формулою (3.42).
Нормативні документи накладають також обмеження на використання виразів (3.47) і (3.48) N
AnRy
Розраховуючи міцність елементів, на які діють осьова розтягувальна сила і згинальний момент, використовують ті ж формули, що й для стиску зі згином (3.42), (3.47) і (3.48), оскільки характер їх роботи та епюри напружень подібні.