ЦЕНТРОВО-СТИСНЕНІ ЕЛЕМЕНТИ. МІЦНІСТЬ І СТІЙКІСТЬ
Міцність коротких центрово-стиснених стержнів розраховують аналогічно до центрово-розтягнених за формулою (3.5), що пояснюється відповідністю діаграм розтягу та стиску металу.
У довгих стиснених елементах несуча здатність вичерпується внаслідок втрати стійкості. Якщо прямий стержень стискати центрально прикладеною силою, то він буде залишатися прямолінійним і навіть при невеликому відхиленні, зумовленому деяким впливом, повертатиметься у попередній прямолінійний стан після припинення впливу. Тобто стержень перебуває у стійкому стані рівноваги. При поступовому збільшенні навантаження стискальна сила досягає такого значення, що будь-яке невелике відхилення стержня від початкового прямолінійного зумовлює швидке зростання викривлення. У цьому випадку осьова сила досягає свого критичного значення.
Значення критичного навантаження і відповідного йому критичного напруження залежить від способу закріплення стержня та геометричних характеристик перерізу. Збільшення кількості зв'язків, якими закріплені кінці стержня, зумовлює підвищення несучої здатності. За основу для порівняння взято стержень з шарнірним закріпленням кінців (рис. 3.2, а). Зміна способу кріплення (рис. 3.2, б, в, г) спричинює зміну форми поздовжнього згину при втраті стійкості. Але її можна привести до основної схеми шляхом заміни дійсної довжини І її розрахунковим значенням Ze[:
Lel = x-l, (3.7)
Де р — коефіцієнт зведення довжини стержня.
|
N_ |
Аналогічним чином впливає жорсткість перерізу. Чим вищий момент інерції перерізу стержня І при сталій площі, тим вища його несуча здатність. Застосуємо відому з курсу опору матеріалів формулу обчислення критичного навантаження
11=1
Н * І
1 І -
Літ -
Рис. 3.2. Розрахункові довжини стиснених стержнів.
Стержня, виведену
Для центрово-стисненого Ейлером:
|
Ішп lef |
Fr,. = п2Е
(3.8)
Перейшовши до критичних напружень Frr U^E ЛпІП
Сг
|
Min А |
А
•ef
ПІП *
Та підставивши радіус інерції г, і гнучкість А = -—,
Lmin
|
(3.9) |
|
О... = |
Одержуємо
7Г£
А2 '
Таким чином, несуча здатність залежить лише від гнучкості стержня, оскільки чисельник — величина стала. Отже, несучу здатність стержня можна підвищити за рахунок зменшення гнучкості, не збільшуючи площі перерізу і, тим самим, матеріаломісткості.
Формула Ейлера справедлива лише для сталих значень модуля пружності металу Е, що спостерігається при великих гнучкостях і напруженнях, менших за межу пропорційності. Водночас розрахунковий опір металу має вищі значення. Теоретичне обчислення критичних напружень дуже ускладнюється, оскільки втрата стійкості проходить при частковому розвиткові пластичних деформацій і змінних значеннях Е. Сьогодні цю задачу розв'язують, використовуючи замість модуля пружності Е зведений модуль Т, за допомогою якого стержень, що працює у пружно - пластичній стадії, замінюють еквівалентним йому пружним ([27], с. 70—77). У нормативних документах критичні напруження рекомендовано обчислювати спрощено як добуток розрахункового опору Ry і коефіцієнта поздовжнього згину <р:
Осг = Ry ■ ф. (3.10)
|
Р=2 / І І, |
|
[1=0, 7 І « • о |
|
Р=0,5 |
|
Jr |
|
С5 II |
Таким чином, перевірка стійкості матиме вигляд
O<otr, (3.11)
Або у розгорнутому вигляді з урахуванням коефіцієнта умов роботи конструкції
Ct = ^<R„-(p-Yc - (3-12)
ГІри обчисленні коефіцієнта ф доцільно використовувати таблиці (наприклад, табл. 1 додатка 8), в яких подано його значення залежно від гнучкості. У нормах також наведені аналітичні залежності з використанням умовної гнучкості:
X = Л (3.13)
Отримані за рекомендаціями норм значення коефіцієнта поздовжнього згину дещо нижчі, ніж за формулою Ейлера. Рівняння Ейлера справедливе для ідеально прямолінійного стержня в умовах центрового стиску. Разом з тим реальні елементи практично завжди мають деяку кривизну, а при завантаженні спостерігаються випадкові ексцентриситети. Це знижує стійкість стержнів і враховується шляхом зменшення коефіцієнта ф.
У дуже гнучких стержнях зазначені випадковості можуть призвести до передчасної втрати
Ь Ь +--------------- ¥ і"-------------------------- 1
Стійкості. Тому нормами встановлено граничні значення гнучкості.
Критичний стан наскрізного стисненого стержня складеного перерізу, окремі частини якого — вітки, з'єднані планками або решітками (рис. 3.3), визначатиметься не тільки гнучкістю власне стержня, а й жорсткістю з'єднувальних елементів (планок чи решіток). Коефіцієнт поздовжнього згину щодо вільної осі приймають, як для суцільних перерізів, за зведеною гнучкістю що враховує податливість з'єднання за допомогою планок чи решіток.
У сталевих стержнях на планках
Kf = Щ + 0,82Xf (1 + п), (3.14)
Або
>,.| = ^ + Хі, (3.15)
Де ку —- гнучкість всього стержня щодо вільної осі у — у, обчислена, як для суцільного перерізу;
, Ц
Л] = — — гнучкість окремої вітки щодо власної осі hi і
Перерізу у, — ylt паралельної вільній (рис. 3.3); Ь b
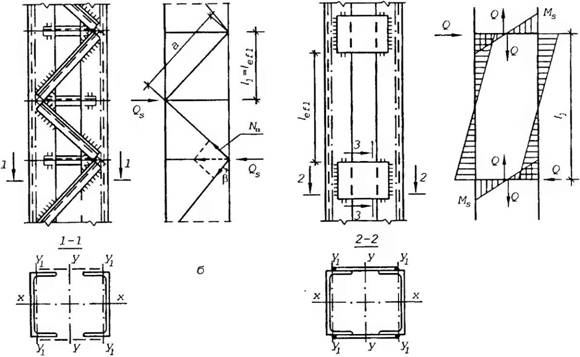
|
Рис. 3.3. Стержні складеного перерізу: а — з решітками: а — на планках; б, г — відповідні розрахункові схеми. |
4---------- f 4-------------- lt,( — розрахункова довжина вітки; г, Уі — радіус
Інерції перерізу вітки відносно осі уі — у2-
Формула (3.14) використовується при співвідношенні погонних жорсткостей окремих віток і планок, що їх з'єднують:
N = (3.16)
Ll ls о
Де /()і та /„. — відповідно моменти інерції перерізів вітки та планки відносно осей г/, — ух та 1—1.
Формула (3.15) справджується при п < - jr.
|
(3.17) |
У наскрізних стержнях складеного перерізу зі з'єднувальними решітками зведену гнучкість обчислюють
Kr = VxJ + (Xj
Ad,
Де А — площа перерізу всього стержня; А(; — площа перерізу розкосів решіток; о^ — коефіцієнт, який залежить від кута розміщення розкосу і визначається за формулою значення коефіцієнта умов роботи yt. = 0,75, оскільки кутник, що є розкосом, кріпиться до стержня колони однією поличкою.
Обчислюючи гнучкість розкосу, використовують найменше значення радіуса інерції кутника. На зусилля N<i розраховують також з'єднання розкосу з вітками колони.
При обчисленні зусиль у планках стержень складеного перерізу розглядають як раму, де стояками є вітки перерізу, а ригелями — планки. Виходячи з рівноваги вузла приєднання ригеля до стояка
Q.,-| = Q-|,
Одержуємо перерізувальну силу в планці:
(3.21)
Q = Q, І
І відповідно згинальний момент:
M = Q|.
(3.22)
(3.18)
Де а, Ь, її — умовні позначки згідно з рис. 3.3.
У стержнях складеного перерізу гнучкість окремих віток не повинна перевищувати 40 та зведеної гнучкості X(.f всього стержня. Коли ж ці умови не виконуються, то можливе руйнування стержня внаслідок втрати стійкості однією з віток перерізу.
Для перерізів, складених з кутників, стержнів з алюмінієвих сплавів та в інших випадках при обчисленні А. ег використовують відповідні рекомендації нормативних документів.
|
А |
|
= 10 |
|
1%' |
Розрахунки з'єднувальних елементів (решіток чи планок) стиснених стержнів виконують на дію умовної гіерерізувальної сили:
За дією цих зусиль перевіряють міцність власне планок, а також засобів їх приєднання.
Перерізи з кутників, швелерів тощо, з'єднаних впритул або через прокладки, перевіряють як суцільні. Але при цьому відстань між прокладками (в просвіті) або між центрами крайніх болтів не повинна перевищувати 40г (і — радіус інерції кутника чи швелера).
У таврових і двотаврових складених перерізах значення г приймають відносно осі, паралельної площині розміщення прокладок, а в хрестових перерізах — мінімальним.
Перевірку стійкості стержня складеного перерізу відносно матеріальної осі х — х здійснюють як суцільного.