Оборудование заводов по переработке пластмасс
Элементарная мощность, рассеиваемая в винтовом канале червяка
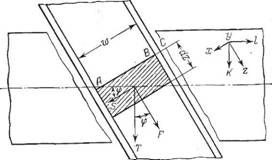
Рассмотрим плоскую модель (рис. 5.26), представляющую собой развертку корпуса и червяка на плоскость хог.
Работа внешних сил расходуется на преодоление сопротивления от сил вязкого трения, возникающих как на поверхности винтового канала (участок АВ), так и в зазоре между гребнем нарезки и стенкой корпуса (участок ВС). Действующая на поверхности стенки корпуса сила dT представляет
|
Рис. 5.26. Схема для расчета мощности, диссипируемой в червяке на участке канала длиной dz. |
Собой векторную сумму сил вязкого трения dF и dS, возникающих в результате существования каждого из этих течений.
Силы вязкого треиия dF и dS, действующие на площадь элемента канала длиной dz, равны »
DF = %zyvadz (5.71>
DS = tx)jwdz (5.72)
Напряжения сдвига, входящие в эти уравнения, определим из выражений
, dvz
Y~h
_ dvx I rin 4UX
= Ч (T) ^ (5.74)
Где Rlz)=eW~™ — коэффициент, учитывающий снижение вязкости за счет разогрева расплава.
Мощность, рассеиваемая на участке канала длиной dz, равна
DW1 = (dF cos ф + dS sin ф) U (5.75)
Подставляя значения dF и dS с учетом уравнений (5.73) и (5.74)-, получим:
DW1 = -------------- jj - [(1 + За) cos2 ф + 4 sin2 ф]dz (5.76)-
Мощность, рассеиваемая в радиальном зазоре, определится из выражения:
DW2 = Uet6R cos фdz (5.77)
Где тек — напряжения сдвига, действующие в зазоре. *
Определяя направления сдвига из закона Ньютона [см. (1.8)], получимї
U2 т)0е cos фdz dW2 = ~~g (5./8)
Итоговая величина элементарной мощности dW, рассеиваемой на участке dz, равна сумме dW и dW2:
DW = drx + dW2 = хф №Adz (5.79>
Где
|
{ |
:W Є )
-jj - [4 sin2 Ф + (1 + 3a) cos2 ф] + J cos ф (5.80)
А N — частота врашения червяка.
Подставим полученное выражение для элементарной мощности в уравнение энергетического баланса (5.55). Далее, заменяя dz на dl/sin ф и пренебрегая величиной QdP (ввиду ее относительной малости), преобразуем уравнение энергетического баланса к виду
ЙТ Чо___ N2di /5 81).
Eb (T-Tg) - QpCp sm<pAdl
Где Ki — дифференциальный коэффициент политропичности, равный
W [(Ть - Т)Кь+ (Ts - Т) %s]
І^ь — коэффициент теплоотдачи расплав — корпус; 7.s — коэффициент теплоотдачи расплав — червяк).
Интегрируя выражение (5.82), получим для небольших значений г�/г[Т— =R(l)< 1,3 (т)о — вязкость при Tg, гт — вязкость при Т), простую расчетную формулу для термонейтрального червяка (taCXb):
Где
Кг=1+2агС (5.84)
А/ = w}4]l(A'<„N2 sin ф) (5.85)
С= 0,5 (Tb + Ts— 2Т) (5.86)
Полученное решение справедливо, если R(l)< 1,3. Это условие означает, ■что приращение температуры в пределах одного Шага расчета не должно превышать 20—25 К (если Ј)f»0,01 К-1)'. В действительности приращение температуры в пределах одного шага расчета составляет от 3 до 5 К. Следовательно, это условие всегда выполняется.
Уравнение (5.84) отражает воздействие основных внешних факторов на ■особенности теплообмена в процессе экструзии. Так, при очень малых значениях коэффициента теплообмена существование перепада температуры между корпусом и расплавом не оказывает никакого влияния на коэффициент поли - тропичности, и процесс протекает в адиабатическом режиме, Ki= 1.
Если же щ велико, то при малых R(l) и больших С (когда средняя разность температур положительна) процесс идет с подводом тепла извне, Ki> 1; напротив, если R(l) велико и средняя разность температур отрицательна, процесс идет с отводом тепла, Ki< 1.
Из уравнения (5.84) следует, что коэффициент политропичности сильно зависит от среднего значения перепада температур, определяемого разностью Ть—Т. Если этот перепад положителен, то в результате дополнительного подвода тепла от стенок корпуса коэффициент политропичности оказывается больше единицы. Если же средний перепад температур отрицателен, то вследствие отвода тепла в окружающую среду коэффициент политропичности оказывается меньше единицы.
В обоих случаях существенное влияние на тепловой поток оказывает коэффициент щ, определяющий относительную долю подводимой извне (или отводимой) энергии по сравнению с энергией, диссипируемой вследствие вязкого трения. Чем меньше щ, тем больше степень термоизоляции системы и тем ■ближе рабочий режим к адиабатическому.
Продольное распределение температур описывается соотношением
Ті+1 = Ті + In (Ri/b) (5.87)
Температура расплава на выходе из червяка также подсчи - тывается из выражения (5.87), только в этом случае вместо текущей координаты / = ЇД/ расчет заканчивается по достижении фактической длины зоны дозирования /д. Очевидно, что каждому значению производительности экструдера при фиксированном значении скорости вращения червяка будет соответствовать ■своя длина зон плавления и питания. Поэтому фактическая длина зони дозирования, которая определяется как разность между общей длиной червяка и суммарной длиной зон питания и плавления, при каждом значении производительности имеет свою величину.
|
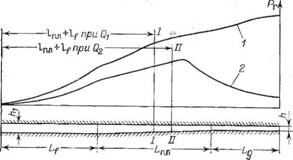
Рис. 5.27. Типичные эпюры давлений при экструзии термопластов при Qi<QKP (кривая 1) и при Q2>Qkp (кривая 2); I—I и II—II — фактические границы зоны плавления; Р, — давление в головке. |
Распределение давлений в пределах зоны дозирования (рис. 5.27) определяется из выражения
DP АI 6nDN cos (pa г|. А/
= ~dF~ 7ігГф +pi=pi+ hib (Ti+1-Tt) - Шу (5.88)
Где Pi — давление в конце предыдущего шага расчета.
Обычно червяки современных экструдеров состоят из двух участков с резко различной глубиной винтового канала, соединенных ступенью сжатия — коротким участком с переменной глубиной канала (длиной от половины до одного'шага).
Некоторые экструдеры оснащаются червяком с ярко выраженной зоной плавления, представляющей собой участок червяка с коническим сердечником, располагающийся между зоной питания и зоной дозирования.
Изменение фактической длины зоны дозирования, вызываемое изменением длин зон питания и плавления, приводит к тому, что реально существующая зона дозирования состоит из двух - участков червяка с различной глубиной винтового канала.
Поскольку объемный расход через поперечное сечение канала остается везде одинаковым (утечками пренебрегаем), изменение глубины канала приводит к тому, что величина а = ~4vlq& по мере уменьшения глубины канала уменьшается, а при очень больших объемных расходах даже изменяет знак.
Объемный расход, при котором на входе в участок зоны дозирования с наиболее мелкой нарезкой градиент давлений меняет знак, удовлетворяет соотношению
QkP>°WV. (5.89)
Где амнн — значение коэффициента а для участка канала с наиболее мелкой нарезкой.
Дальнейшее увеличение производительности приводит к тому, что давление проходит через максимум. При этом эпюрз Давлений приобретает вид, подобный кривой 2 на рис. 5.27.
Если производительность участков канала, расположенных 'ближе к зоне плавления, оказывается чрезмерно велика, возникающий при этом положительный градиент давления автоматически приводит к ее уменьшению. Аналогичным образом при недостаточной объемной производительности участка червяка с коническим (или цилиндрическим) сердечником избыточный расход обусловливает возникновение отрицательного градиента давлений.