Моделирование температурных полей в ограждениях методом элек’гро’геплоаналогии
При исследовании стационарной теплопроводности в твердых телах методом ЭТА основанием для замены температурного поля электрическим служит математическая и физическая аналогия между теплопроводностью в твердом теле и распространением электрического тока в электропроводной среде. Эквипотенциальным линиям в модели соответствуют изотермы в исследуемом твердом теле (рис. 10-1). С линиями токов они образуют ортогональную тепловую сетку, которая дает картину распределения полей температур и тепловых потоков в исследуемой конструкции. В практике широко распространены модели из электропроводящей бумаги. При построении модели должны выполняться следующие требования теории подобия:
1. Электрическая модель должна представлять узел в некотором масштабе, геометрические размеры которо
|
V |
<р |
|||||||
|
N |
||||||||
|
Ч |
N |
|||||||
|
5' |
||||||||
|
Rj |
N |
|||||||
|
Ч |
||||||||
|
И |
|
БО |
ГО связаны коэффициентом геометрического подобия kfl
(10-1)
Где и I — геометрические размеры модели и натуры.
2. Удельное сопротивление модели должно быть обратно пропорционально коэффициенту теплопроводности натуры при постоянстве физического коэффициента подобия в любой зоне исследуемой конструкции:
|
Рис. 10-1. Теплопроводность составного ограждения. |
К = (10-2)
Где р — удельное поверхностное сопротивление квадрата электропроводящей бумаги, Ом[6].
3. Граиичиые условия для модели и иатуры должны быть подобны, т. е. потенциалы в любой точке должны быть связаны с температурой соответствующей точки иатуры коэффициентом подобия теплового состояния kt:
Т~фмин, (10-3)
|
I — изоляция; 2 — теплопроводное включение; 3 — изотерм»: 4 — линии теплового потока; 5, 6 — распределение температур по толщине ограждения соответственно в сечениях 1-І н //-//. |
T---- 'мин
Где ф, фмин — потенциал Е любой точке модели и минимальный потенциал; t, н — температура в некоторой точке модели н минимальная температура.
При моделировании удобно пользоваться не значением потенциала ср, выраженного в вольтах, так как при этом нужна стабилизация питающего напряжения, а приведенной единицей потенциала. В качестве приве
денной единицы можно принять значение, равное 1% напряжения питающего устройства. Если максимальный и минимальный уровни потенциала модели будут составлять Фмакс=100% И ф„11Ш = 0, то выражение (Ю-З) примет вид:
•макс 'мин
Из выражения (10-3) следует, что если принять при 4>мви=0 tme—to (где 4 — температура среды, с которой происходит теплообмен), то электрический потенциал (р, замеренный в любой точке модели, отобразит в некотором масштабе избыточную температуру в данной точке натуры:
Если учитывать, что избыточная температура представляет разность t—t—to, искомые значения t могут быть вычислены по формуле
T = ф(<»"",с~'°) -f L. (10-6)
100
Прн моделировании тепловой работы ограждений наиболее часто встречаются следующие граничные условия: теплообмен по границе отсутствует-^- =0; за-
Dn
Дана постоянная температура q>=const; значение температуры меняется вдоль границы cp=f(S); задан теплообмен постоянной интенсивности со средой 0=const; теплообмен вдоль границы имеет переменную интенсивность q=f(S), где S — граница моделируемой области.
Наиболее просто реализуется граничное условие = о. Для этого вдоль рассматриваемых участков
Дп
Обрезают электропроводную бумагу и преграждают путь току в направлении нормали к данной границе. Для реализации граничного слоя <p=const на заданном участке необходимо приклеить шины из фольги и подать на ннх напряжение с нужным потенциалом. На участках границы, где потенциал <р является функцией длины границы S, вдоль границы области приклеивается полоска фольгн, разрезанная по длине S на п участков, внутри
каждого из которых потенциал будет оставаться постоянным. Подключая выход декад делителя напряжений к соответствующим участкам, можно добиться требуемого распределения ф по границе. Граничное условие теплообмена 17—const выполняется просто. Термическое сопротивление перехода теплоты от поверхности к среде с температурой t0 моделируется полосой электропроводной бумаги, ширина которой 6 при заданном коэффициенте теплоотдачи от стенки к среде а, определяется по формуле
Б = -г———, (10-7)
Где р,- — удельное сопротивление бумаги.
В тех случаях, когда задан радиационный теплообмен в топочной камере, например, при моделировании тепловой работы ошипоианного экрана, ои может быть условно сведен к конвективному теплообмену с использованием формулы Ньютона:
9 = (Ю-8)
Где <ф — заданная температура факела; t — замеряемая температура поверхности.
Значение а, неизвестно, и его подбирают методом последовательных приближений путем сравнения значений теплового потока, рассчитанных по формуле (10-8) и по уравнению Стефана — Больцмана.
Граничное условие q=f(S) встречается редко, например, в задачах по лучистому теплообмену, где распределение теплового потока от факела по периметру трубы определяется угловым коэффициентом освещенности. Изложение более сложного способа реализации подобного граничного условия дано в [10-1] и здесь не приводится.
|
Рис. [0-2. Принципиальная схема Моделирования методом ЭТА. |
Конструктивно модель представляет собой плоское сеченне исследуемой обмуровочной конструкции, выполненной из электропроводной бумаги с различным удель
ным сопротивлением. Отдельные участки модели склеиваются на ширине 2—3 мм между собой электропроводным клеем.
Принципиальная схема моделирования методом ЭТА с помощью электроинтегратора ЭГДА-9-60 показана на рис. 10-2. Интегратор / представляет собой измерительный мост постоянного тока с выпрямителем для питання
|
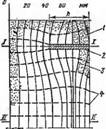
Рис. 10-3. Моделирование температурных полей составного узла ограждения. / — жаростойкий бетон: 2 — изоляция; 3 — газе плоти а я штукатурка; 4— каркасная рама плиты. |
От сети переменного тока. В схему интегратора входит необходимый для моделирования потенциометрический делитель напряжения. Измерительное устройство 2 выполнено в виде отдельного малогабаритного блока. С помощью щупа 3 измерительного устройства производится снятие промежуточного значения потенциала в заданной точке модели 4.
Для представления процесса моделирования рассмотрим конструкцию обмуровки (рнс. 10-3), состоящую из слоев жаростойкого бетона Ї сложной конфигурации, изоляции 2 и наружной газоплотной штукатурки 3. Рама щита обмуровки 4 находится в слое изоляции. Условия работы обмуровки н теплофизические характеристики следующие: температура на внутренней поверхности *Вн=650°С; окружающего воздуха *В = 25°С; коэффициент теплоотдачи от обмуровки к воздуху а=10 ккал/(ч-м2'°С); коэффициент теплопроводности материалов: металла? ц=40, изоляции Я2=0,1, бетона Я3=0,9 и штукатурки ^4=0,5 ккал/(м-ч-°С). Геометрические характеристики узла обмуровки показаны иа рис. 10-3.
Требуется найти распределение температуры по сечению конструкции, наружную температуру обмуровки и тепловые потери в окружающую среду с учетом теплопроводных включений. Предварительно найдем величину q, произведя расчет данного узла обмуровки без учета теплопроводного включения:
________ tKH — tB______________ 650 — 25______
Q~ ^ , Да, fid, 1 "0,26 0,1 0.015 1 Яа ?і3 ^ а 0,1 0,9 0,15 + 10 = 220ккал/(ч-мв).
Зная тепловой поток через обмуровку q, определяем температуру наружной поверхности обмуровки /н:
= — ? = 25 + 22 = 47°С. а
Для моделирования тепловой работы конструкции с учетом тепловых «мостов» берем участок, ограниченный вертикальными осями симметрии, условно перенеся стенку швеллера рамы по центру его полки. В данном случае поле температур двумерное, т. е. t=f(x, у). Граничные условия задачи: теплообмен по вертикальным осям симметрии отсутствует, постоянство температуры по внутренней поверхности и конвективный теплообмен по наружной поверхности. Так как погрешность измерений уменьшается при увеличении масштаба модели, считается, что площадь модели должна быть не менее 200 см2. В нашем случае конструкция имеет небольшие размеры н можно взять масштаб т=1/1. При этом масштабный коэффициент ki, вычисленный по формуле (10-1), будет равен единице. Далее подбираем бумагу для изготовления модели. Так как теплопроводность материала и электропроводность бумаги обратно пропорциональны, выбкраем для изоляции с ^2=0,1 ккал/(м-ч-Х) бумагу с максимальной электропроводностью (в нашем случае р2=100 кОм). Коэффициент подобия для всей модели, вычисленный по формуле (10-2), составляет:
H= ~ . .L»^ = Ю-4 ч• м• °С/(ккал• Ом).
К 0,1-100000 1 '
Из этой же формулы, учитывая постоянство для всей модели, находим значение р для остальных зон модели:
= - тД—=------------------------- =250 Ом = 0,25 кОм;
W ю-«-40
Рз = 10 кОм и р4 = 20 кОм.
Коэффициент теплоотдачи моделируем полосой электропровод - нон бумаги. Ширина полосы при принятом р—12,5 кОм вычисляется по формуле (10-7):
{=7^ = 10-МО! І2.5.10* = 0'08М-
А) 0,3
|
Б) |
Средняя температура наружной поверхности обмуровки с учетом влияния теплопроводного включения (рис. 10-4,6) составляет /ср=53°С.
Потеря теплоты в окружающую среду с учетом тепловых «мостов» составит:
= a (tcv — /в) = 10 (53 — 25) = 280 ккал/(ч - м2).
|
Обычно моделирование а производится полосой из бумаги, одинаковой с бумагой для модели, что позволяет избежать лишней склейки. В данном случае это привело бы к слишком узкой полоске и могло бы вызвать большую погрешность. Для моделирования отвода теплоты перпендикулярно поверхности полоса для а разрезается в поперечном направлении на полоски шириной 5—10 мм. Для предотвращения электрического контакта между ними в прорези вкладывается лист обычной бумаги. Детали модели вырезаются в масштабе 1:1с необходимым припуском на |

|
= ее |
|
Рис. 10-5. Характер влияния относительной глубины включения hjH на (рмвкс обмуро - вочной конструкции (s=0,5 мм; 6— = 0,0025 м; ВІ2 = 15; Х, Д2=390). |
Превышение потерь теплоты по сравнению с плоской однородной стенкой составляет:
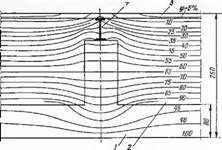
Рис. 10-4. Распределение температур в модели.
С —по толщине ограждения; б —по наружной поверхности ограждения; 1 — по оси включения; 2 — на участке максимального удаления от включения.
Склейку. При изготовлении модели у выбранной бумаги проверяется ее удельное сопротивление. Так как оно неоднородно возле краев рулона, прн изготовлении модели целесообрано отступать от края примерно иа 100—150 мм с каждой стороны. Места склейки модели разглаживаются и прижимаются грузом. Фольга перед приклеиванием к бумаге обезжиривается спиртом. Полное высыхание клея происходит через 5—7 ч. После изготовления модель зажимают в шины и к внутренней поверхности ограждения подводят электрический ток с потенциалом, равным 100%, что соответствует температуре ограждения 650°С, и к полосе, моделирующей а с нулевым потенциалом, что соответствует температуре воздуха /„=25°С. Установив иглу интегратора (щуп) в любую точку модели, с помощью измерительного устройства получаем значение потенциала. Распределение эквипотенциальных линий (изотерм) в модели с учетом теплопроводного включения показано на рис. 10-3. На рис. 10-4 показано распределение температур по наружной поверхности, по толщине конструкции в районе теплопроводного включения и иа участке максимального удаления от него. Пересчет замеренных значений потенциалов в температуру ведется по формуле (10-<5). Например, максимальное значение потенциала, замеренное на наружной поверхности модели по оси теплопроводного включения, составляет <р=13,9 В, что в пересчете по упомянутой формуле дает:
.3,9(650 - 25) 100 " 100
Приведенный пример показывает простоту метода моделирования, его преимущество над сложными аналитическими расчетами.
На ЗиО были проведены исследования температурных полей методом ЭТА [10-3] по методике, разработанной ОРГРЭС. В программу исследований входило изучение влияния теплопроводных включений прямоугольной формы на распределение температур по наружной поверхности составной обмуровочной конструкции. Результаты исследований показали, что максимальная температура иа наружной поверхности обмуровки fMавс практически ие зависит от шага включений. Для несквозного включения нз металла максимальная температура наружной поверхности обмуровки зависит не только от глубины включения, но и от его местоположения. При расположении включения с наружной стороны изоляции (например, укрытие наружной швеллерной рамы в слое изоляции) рост локальных температур изоляции вблизи включения более интенсивен. Зависи - Іость /м,1кс от местоположения включення показана на рис. 10-5. Кривая 1— включение расположено с наружной стороны ограждения, кривая 2 — с внутренней.