ОЦЕНКА ВЛИЯНИЯ МЕТАЛЛИЧЕСКИХ ВКЛЮЧЕНИИ
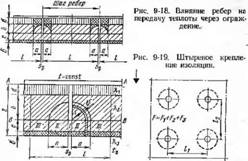
В современных натрубных обмуровках применяются ребра н штыри, служащие для креплення изоляционных материалов. Ребра (рис. 9-18) и штыри (рис. 9-19) располагаются в определенном порядке с постоянным тагом. Расчет ограждений с металлическими включениями сводится к оценке их влияния на потери теплоты по сравнению с ограждениями без включений. Решение такой задачи при определенных допущениях возможно только для правильного и регулярного расположения в обмуровке металлических ребер и штырей. Для расчета потерь теплоты через стеику с ребрами делают следующие допущения [9-6, 9-7]:
1. Температура ребра постоянна по его длине и ширине н равна температуре основания.
2. Тепловой поток от боковых поверхностей ребер идет по цилиндрическим поверхностям, центральная' ось которых лежит в основании двугранных углов ребер (рис. 9-18).
|
|
3. На участках стенки вне цилиндрических поверхностей тепловой поток не искривлен и распространяется прямолинейно. При этом сопротивлением между ребра - 'ми и обмуровкой пренебрегают и считают, что теплообмена на границах зон не происходит.
Рассматривая общий случай, выделим участок стенки высотой Н— I м с ребрами. Ширину стенки принимаем равной шагу I между ребрами. При принятых допущениях ширина стенки I делится на три зоны (рис. 9-18), каждая из которых соответствует своему тепловому потоку. Зона /—Fi=Sp (толщина ребра); зона II—F2=2a; зона III—F3 = l—sp—2а.
Площадь выделенного участка, м2:
F = F1 + F, + F, = Hl = l.
Через каждую зону проходит свой тепловой поток, полная величина теплового потока для выделенного участка:
<? = & + & + ft.
Ширина зоны //, равная 2а, находится из условия, что тепловой поток всегда распространяется по кратчайшему пути: от линии А-А (основания ребра) до линии В-В (конца ребра) (b+d), поэтому радиус а внешней поверхности потока теплоты от ребра найдется из равенства термического сопротивления дуги Jto/2 н толщины слоя fc-j-d:
Пс d ^ b 2/.^ 7-і Я* в
Откуда получим:
Это равенство справедливо при условии что
Обычно имеет место.
Нетрудно видеть, что при принятых допущениях в объеме изоляции, показанной двойной штриховкой, теплообмен отсутствует. Термическое сопротивление:
Для зоны /
Для зоны III
R — d | | 6 | 1
Яі Яга Яд ttg
Полное термическое сопротивление зоны //
+ _!_. (9-32)
ОЇ 1 I ап^з, .1 «в
Если известны температура t, па уровне А-А, температура внешней среды tО и термические сопротивления каждой из зои Ri, Ru, Rш, то потери теплоты и наружные температуры /„,, 1„2 и t, a определяются по соответствующим тепловым потокам:
Л h—lg. П - ^ "t,! . п tl
Потери теплоты, отнесенные КІМ2 ограждения (при Н= м),
|
|
Q_ Q.+Qs+C»
Прн расчете потерь теплоты через стеику со штырями (рис. 9-20) будем исходить нз тех же допущений, что и прн расчете ребер, откуда следует, что тепловой поток от штырей распространяется по сферическим поверхностям. Выделяем участок стены F, на котором расположено II штырей, и делим его на три зоны. Площадь первой зоны F,=nf, где f~nd2/i~ площадь сечения одного штыря. Площадь второй зоны
Рнс. 9-20. Влияние шты-
_ я (д2 — (Р) ревого крепления на пе-
Са — 11' 7 ' редачу теплоты через
Ограждение.
Где о — радиус внешней сферической поверхности; Fa'~F—(Fi~hF2) —площадь третьей зоны.
Радиус внешней поверхности находится из условия кратчайшего пути теплового потока
—----- — = Ь,
2 2
Откуда
2b+d
Так как диаметр штыря d мал по сравнению с величиной 2Ь, то для упрощения вывода можно принять, что г=о«2Ь/я.
|
Поверхности |
Термическое сопротивление второй зоны Л'; находится также, как и для ребра.
|
(9-33) |
Полное термическое сопротивление второй зоны
. n'(a'-dZ) И'- «1(4 Ь-nd)
Диаметр штыря d по сравнению с размерами а и b мал, и им можно пренебречь. Тогда
Где Rm'c — термическое сопротивление слоя штукатурки.
Примеры расчетов ограждений с теплопроводными включениями рассмотрены ниже.