Моделирование миграции подземных вод
Модели гетерогенно-блоковой среды
Для горных пород характерна гетерогенность различных масштабов— от кристаллической решетки до массива. Для описания процессов переноса наиболее значимой является гетерогенность порядка десятков сантиметров, обусловленная литолого-фациаль- ной изменчивостью и трещиноватостью горных пород. Для ее учета при построении теоретической модели переноса используется расчетная схема (модель) гетерогенно-блоковой среды с двойной емкостью, представляющей собой квазиоднородную систему слабопроницаемых блоков, равномерно прорезаемых проводящими каналами.
В карбонатных породах такие каналы представлены наиболее крупными трещинами (объемное содержание порядка 1 %), а блоки представлены весьма слабопроницаемым карбонатным материалом с пористостью 10—15%. Такая гетерогенно-блоковая среда называется также порово-трещинной. В глинистых породах проводящие каналы —это зоны, повышенная проницаемость которых объясняется наличием более грубого материала, а также повышенной трещиноватостью, причём проницаемости каналов и блоков не имеют резкого различия. Такая гетерогенно-блоковая среда может быть названа также мозаичной.
В модели порово-трещинной среды перенос в трещинах (каналах) осуществляется конвективным путем, а в блоках —диффузионным. Рассматривая перенос в блоке, выделим начальный период, когда на поток переноса не влияет размер блока, который в этом случае можно считать неограниченным (схема неограниченной емкости блока), и квазистационарный период, когда диффузионный перенос в пределах блока можно рассчитывать по схеме - соср°доточенной емкости, усредняя («размазывая») процесс переноса внутри блока, т. е. считая емкость блока как бы сосредоточенной в его центре.
У. Гарднер и Р. Брукс предложили использовать для решения задач солепереноса модель гетерогенной среды с сосредоточенной емкостью. Они выделяли «мобильные» (двигающиеся вместе с водой) и «иммобильные» (отстающие от потока) соли, причем удельная плотность обмена между ними (в единице объема породы) и* принималась согласно уравнению и* = а*(ст—сіт), где - а* — коэффициент обмена; Cm и Сїт — концентрации мигранта в мобильной и иммобильной воде соответственно. Таким же уравнением описывается внутренний обмен в модели двойной (дифференциальной) пористости, согласно которой пористая среда представляется в виде системы проходных и застойных («тупиковых») пор, причем эта модель рассматривается в качестве альтернативной по отношению к модели гидродисперсии [И, 80]. Вместе с тем для лучшего понимания процесса представляется важным обоснование такой модели на основе блокового строения пород,, что открывает возможности оценки связей параметра массообмена с геометрическими характеристиками среды.
Наиболее полное и ясное физическое представление о гетерогенной среде с сосредоточенной емкостью дает рассмотрение м о - заично-блоковой среды, которая представляется как квазиоднородная. Такой постановке соответствует система блоков,, равномерно прорезаемых проницаемыми каналами, причем конвективный поток в извилистых проницаемых каналах равномерно обтекает слабопроницаемые блоки и частично протекает через них (рис. И), Таким образом, в этой модели предполагается, что продольный перенос в проводящих каналах осуществляется только конвективным путем, а обмен между каналами и блоками — диффузионным и кондуктивным по схеме сосредоточенной емкости блока.
Уравнение внутреннего обмена между каналами и блоками здесь составляется на основании баланса мигранта в элёментар: ном объеме породы, содержащем один блок и относящиеся к нему проницаемые каналы. Обозначая концентрацию мигранта в каналах через с, а в блоке через с*, запишем выражение для расхода поступления мигранта в блок диффузионным путем: Qd = = £)м©б((с —с*)//б, где ©б — средняя площадь поверхности блока; /б — расчетная длина диф - фузионно-кондуктивного переноса в блоке.
Кроме того, конвективным путем происходит перенос при скорости фильтрации в блоке Об=£бО (где — относительная проницаемость блоков), так что расход QK конвективного поступления мигранта в блок определяется выражением Qk = г>бЮб'(с — с*), где соб/ — площадь горизонтального сечения блока. Составим баланс мигранта в блоке объемом Fe:
Ал —т~ + (с — С*) =-пУй —- , h ot
Откуда получим уравнение блокового обмена в виде
П* *(С — С%
Dt
Где п* — пористость блоков; а* — коэффициент блокового обмена, который с учетом диффузионных и конвективных составляющих ■а*а и а*к имеет вид
А* - а/ + у. к:':'- = а/ + XKv, (4.1 2)
Где v — скорость фильтрации.
Коэффициент диффузионного обмена a*d и параметр конвективного обмена Як связаны с удельной поверхностью блоков соотношениями
V - ^ = хЛ$*2; хк - ^f - 7.AS,, (4.13)
|
|
|
Е2* & & ЕЕк |
|
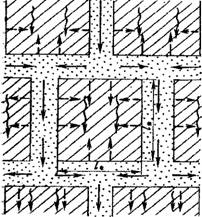
Рис. И. Схема мозаично-блоковой среды: 1 — проницаемые каналы; 3 — слабопрони - •цаемые блоки; 3 и 4 направления конвективного переноса в каналах и блоках соответственно; 5—направлення диффузионного переноса в блоках |
Где %d= (Us*)~[8] и Хк=(о'б/юб— коэффициенты, зависящие от формы блоков; s* — удельная поверхность блоков. Теоретическим анализом Диффузионного переноса в телах различной формы устаиав - «4
ливается, что для шаровидных блоков %d=0,5, для пластинчатых Xrf=2/3, а для блоков кубической формы можно считать Хк=1/6.
При изучении процессов солепереноса в супесчано-суглинистых монолитах было установлено [39], что обычно KkV>a*a, т. е. во внутриблоковом обмене здесь превалирует конвективный перенос, причем получены значения Як= (1 —10) м-1. Для трещинно-поро - вых сред (например, карбонатных пород), характеризующихся малой проницаемостью блоков, а* = а*а-
Для гетерогенной среды с неограниченной емкостью блоков удельная плотность внутриблокового обмена и** записывается на основе интеграла Дюамеля [39]:
____ t
Й**=р*с»'; = <V = T? J^=h (4-14)
О
Где п* и s°* — соответственно пористость и удельная поверхность блоков; t — время от начала процесса; D*M — коэффициент диффузии мигранта в блоках.
Для оценки условий применимости схем сосредоточенной и неограниченной емкостей блоков в квазиоднородной среде рассмотрим условия симметричного диффузионного переноса в блоке пластинчатой формы толщиной 2т0. В этом случае поперечный перенос в блоке описывается Дифференциальным уравнением одномерной диффузии їв направлении г, решение которого в изображениях по Лапласу—Карсону при граничных условиях С—С0, г—0, dC/dz =0, z=m0 и начальном нулевом условии дает следующее выражение для плотности поперечного переноса Сг на границе разделяющего слоя:
С/ = • с/, с/ = т0 th то, т0 = т0 Vnp DM, (4.15)
То
Где р — параметр преобразования. В частности, для схемы неограниченной емкостиcz'=m0 устанавливается, что с ..погрешностью до 10% она применима при >1,5.
Для схемы сосредоточенной емкости Со —С*
С г = Ai ------------ — , (4.16)
Щ*
Где С* и С0 — изображения средней концентрации мигранта в блоке и в проводящем канале соответственно; т0* — средняя длина пути диффузионного переноса в блоке. Уравнение баланса мигранта в блоке, записанное в изображениях, при этом будет
С» —С*
--------- ;----- = поторС*. (4.17)
Щ
|
То ) |
Выражая С* из формулы (4.16) и подставляя в формулу (4.17), после алгебраических преобразований получим
пластинчатой формы доказывается применимость схемы сосредоточенной емкости при условии т<1, причем следует задавать mo* = 0,33mo.
Сопоставление условий применения схем неограниченной и сосредоточенной емкостей показывает, что при расчетах в интегральных изображениях эти схемы практически стыкуются при размерах блока, удовлетворяющих условию
2m0 = (2-3)/Z)M/K/>). (4.19>
Для расчетов в реальном времени в условии (4.19) можно сделать замену p=\/(nt), которая следует из сопоставления решений в изображениях и оригиналах при постоянной концентрации мигранта в проводящих каналах. Тогда выражение для размера блока, разграничивающего применимость схем неограниченной и сосредоточенной емкостей блоков, примет вид
2т0 = (2-3) V*DJIn0 , (4.20)
Где t — расчетная длительность процесса. Для блоков неправильной формы в качестве геометрической характеристики целесообразно принимать удельную поверхность блоков по отношению к объему породы s*, причем для блока пластинчатой формы $*= = /п<г1.
Подставляя в уравнение (4.20) m0=s*~\ получим выражение для времени t*, определяющего условие применимости схем неограниченной и сосредоточенной емкостей (соответственно при t<t* и t>t*): t* = (0,15—0,3)n0/s*2DM).
Аналогичный критерий, но с несколько большим числовым коэффициентом (примерно в два раза) дается в работах [23, 31].
Заметим, что условия применимости схемы с сосредоточенной емкостью могут оказаться более широкими, если учесть заведомую условность представления породы как квазиоднородной среды, а также внутреннюю неоднородность блоков и, в частности, что поверхность блоков горных пород может обладать существенно пониженной диффузионной проницаемостью, обусловленной мета - морфизацией пород при обменных физико-химических процессах.