ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

НЕЛИНЕЙНЫЕ ФЕРМЕНТАТИВНЫЕ ПРОЦЕССЫ

В ферментативных процессах могут проявляться различные типы нелинейных зависимостей от концентраций реагентов; в частности, удается наблюдать и периодические ферментатив­ные реакции (см. § 8.7).

Стационарная кинетика ферментативных процессов может быть нелинейной в смысле нелинейной зависимости скорости превращения субстрата от его концентрации, а также от кон­центрации других эффекторов. С такими ситуациями мы встре­чаемся при рассмотрении белков-ферментов, обладающих чет­вертичной структурой и имеющих несколько активных центров, поведение которых взаимозависимо. Указанная нелинейность служит выражением кооперативности системы и проявляется в наличии особенностей (перегибов и максимумов) на кривых зависимости стационарной скорости от концентраций лигандов. Эти явления, весьма существенные для понимания свойств алло - стерических ферментов, рассмотрены в §§ 7.5, 7.6 книги [9]. Од­нако нелинейность стационарной кинетики в этих случаях никак не означает удаленности системы от состояния равновесия — она возникает и при равновесных соотношениях фермента с ли - гандами. В модели Моно, Уаймана и Шанжё (модель МУШ) [9, 50, 51] присоединение лигандов приводит лишь к сдвигу равновесия.

Рассмотрим неравновесный ферментативный процесс. Не- равновесность возникает в результате значительных различий в скоростях конформационных изменений ферментов, которые могут быть большими и малыми по сравнению со скоростями связывания субстратов и образования продуктов. Как уже ска­зано, классические модели аллостерических ферментов основаны на допущении быстрого наступления равновесия между всеми формами фермента, отличающимися друг от друга коиформа - циями и степенью насыщения лигандами. Однако во многих случаях изменение конформации оказывается наиболее медлен­ной, определяющей кинетику стадией. При этом стационарная реакция протекает вдали от равновесия, что и приводит к спе­цифическим особенностям на кривых зависимости скорости ре­акции от концентраций лигандов. Эти особенности нельзя ин­терпретировать на основе равновесных моделей.

Кинетические проявления конформационных изменений были проанализированы для одноцентрового мономерного фермента в ряде работ [52—56]. Однако во многих случаях за своеобраз­ное кинетическое поведение ответственны скорее медленные из­менения четвертичной структуры олигомерньгх ферментов. В ра­боте [57] рассмотрены их нелинейные свойства.

Модифицируем модель МУШ. Рассмотрим фермент, моле­кула которого содержит п субъединиц — протомеров. Молекула фермента может находиться в двух различных конформацион­ных состояниях R и Т, в которых она имеет различное химиче­ское сродство к лиганду S.

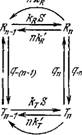
Будем считать, что переходы между этими состояниями про­исходят значительно медленнее, чем связывание и освобожде­ние субстрата и образование продукта. Схема реакции представ­лена на рис. 8.27.

В неравновесном стационарном процессе фермент испыты­вает циклические конформационные изменения. Он лучше свя­зывает субстрат в одной конформации, чем в другой, в которой он легче освобождает продукт, после чего возвращается в ис­ходное конформациониое состояние (ср. стр. 320). При равно­весии конформеров, которое описывается условием (смысл
констант ясен из рис. 8.27)

KRjkT =

Циклические конформационные превращения отсутствуют.

Пхт

KT. x r

В модели МУШ предполагается, что лимитирующими яв­ляются стадии образования продуктов с константами скорости

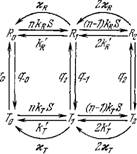
Рис. 8.27. Схема реакции, катализируемой «-мерным ферментом, имеющим два конформационных состояния.

Хд и хт. При этом стационарный процесс соответствует равнове­сию всех конформационных состояний фермента Ru ТПредпо­ложим, что равновесия нет, скорости переходов Ri Tt яв­ляются наименьшими (S — концентрация субстрата)

K~St k „S; k R,

При этих условиях в стационарном процессе соотношения кон­центраций фермента в состояниях Ri/Rj, TJTj определяются только концентрацией субстрата и константами K'R = kRj(k'R-\- xR)

И К'т — k'Tj{k'T + хг), но не константами Ці, q~i. Предполо­жим далее, что концентрация продукта мала, следовательно, можно пренебречь стадией его связывания. Это упрощение не принципиально. Скорости конформационных переходов опреде­ляют только отношение общих концентраций фермента в двух конформациях Rt/Tt, где

(8.80)

Г=0

В са

Мом деле,

Rt — 2 Ri,

(K'Rsy,

(K'rSу.

Яо

Л

То

(8.81)

І)

П (п

П (п - 1) ... (п - і)

1-2 ... і - 1) ... (я - 1-2 ... і

Условие стационарности процесса можно записать в виде

І R,,,= t (8.82,

Из равенств (8.80) — (8.82) следует

І п (п — 1) ... (п — і)

1-2 ...і

І=0

(8.83)

*T (] + KRS)

Rt О + ФГ

I=0

Условие детального баланса при равновесии приводит к законо­мерному изменению констант равновесия qjq-i в зависимости от индекса І:

Її _ % 4-і <7-о

. і

(£) • <8-84>

Где Kr — knjk'n, Кт = кт1кт.

Допустим, что константы ^ и изменяются монотонно по мере связывания субстрата активными центрами. Тогда в силу (8.84) получим

Ч{+1 = а _ 1 Яі Кт s

И (8.85)

Ч—(»-Н) а

—і

Где а, s, г — константы.

Для системы глицеральдегидфосфатдегидрогеназа - f - НАД обнаружено именно монотонное изменение констант qf, при­чем s = 25, г = 1 [58].

У-

С помощью (8.85) получаем из (8.83)

Rt <7-о _ Г(* + /)(г* + 1)-|"

Где x — KrS/г — безразмерная концентрация субстрата и I — — (1 + + xR/k'R). Величина Rt/Tt изменяется от q0/q_0

При S = 0 до qnlq-n при S-*-oo. Для равновесной модели МУШ Rt/Tt монотонно зависит от S [59]. При равновесиях происходит монотонный переход фермента из одной конформации в другую, обладающую большим сродством к субстрату.

Вдали от равновесия при определенных значениях пара­метров г, s, I функция у{х) может быть немонотонной. Допу­стим, что две конформации отличаются каталитической актив­ностью, но не сродством к субстрату, т. е. г = s. В этом случае функция у(х) проходит через максимум, а ее предельные зна­чения при х = 0 и х —V оо совпадают. Если г ф s, то у(х) про­ходит через максимум, а предельные значения разнятся. При г = 100, s = 150, / = 2 и п — 4 максимум у(х) отвечает х = = 0,1. Это означает, что при увеличении х сначала происходит переход Г->- а затем переход R -> Т. Такое переключение кон - формационного перехода может проявиться в виде промежуточ­ного плато на кривой зависимости стационарной скорости реак­ции от концентрации субстрата S. Формула (8.86) показывает, что немонотонность у(х) возможна при отличии параметров г, s, I от единицы.

Начальная стационарная скорость реакции, отнесенная к полной концентрации фермента Rt - f - Tt, равна

П п

XR Z iRi + ХГ Z ІТІ

"Ч+Г,"' ■ (8-87)

Для рассматриваемой модели это выражение приобретает вид

/ ч KRLrx (гх + 1)"-' (X + /)" + XTSX (sx + /)"-' (X + 1) °oW— L(rx+ I)" (x + /)" + (sx + (х + 1)" '

Где L — qo/q-o — аллостерическая константа равновесия. Кри­визна получаемых кривых Уо(х) больше, чем в случае равновес­ной модели МУШ, так как концентрация субстрата х входнт в уравнение (8.88) в степени 2п, а в соответствующую равно­весную функцию только в степени п. Равновесная функция по­лучается из (8.88) при /= 1, она совпадает с формулой для модели МУШ [50]. Рассматриваемая модель учитывает два типа нелинейности — нелинейность, определяемую равновесными ко­оперативными свойствами, и нелинейность, вызванную медлен­ностью конформационных превращений, т. е. удаленностью от равновесия.

Вследствие неравновесности на кривой v0(x) может появить­ся промежуточное плато. Соответствующая кривая v(x), полу­ченная при параметрах xR/xT — 0,1, L = 10, 1 = 4, г = 100, s = 150, п = 4, показана на рис. 8.28. Плато получается в об­ласти х= 1. Такая кривая может вырождаться в S-образную кривую или в кривую, лишенную особенностей. Равновесная модель МУШ объясняет только S-образнне кривые v(x) при
любом числе состояний фермента и любом числе субъединиц п [60].

Для п = 4 кривые с промежуточным плато могут быть полу­чены на основе равновесной модели последовательных конфор­мационных изменений Кошланда [61]. Однако при этом прихо­дится вводить искусственное предположение о резком измене­нии характера кооперативности — замене отрицательной коопе­ративности на положительную при увеличении концентрации субстрата. Впрочем, для любой равновесной модели концентра­ция субстрата входит в выражение скорости реакции в степени, не стар­шей п. Поэтому и модель Кошлан­да не всегда согласуется с опытом [62].

Неравновесная модель очень чувствительна к значениям пара­метров и дает большое разнообра­зие кинетических кривых. Можно думать, что сходные ферменты, по­лученные из различных источников (например, глицеральдегидфосфат- дегидрогеназа из дрожжей, из мышц животных и насекомых), про­являют различный характер коопе­ративности именно вследствие не­равновесности своего поведения. Медленные изменения конформации могут приводить к пред - стационарному нарастанию или спаду активности фермента [56]. Приближение к стационарному состоянию может быть не­монотонным, в частности иметь характер затухающих колеба­ний вследствие неравновесности (см. также [63]).

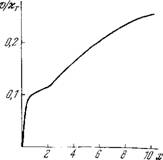
Рис. 8.28. График стационарной скорости с промежуточным плато.

Следует подчеркнуть, что однонаправленность циклического ферментативного процесса возможна только в кинетическом ре­жиме, вдали от равновесия. Ни одна из элементарных стадий цикла не может быть истинно необратимой. Поэтому примене­ние термина «релаксация» (см. § 6.6) условно. На первый взгляд может показаться, что прямая и обратная реакции S -*■ Р н Р -> S способны идти разными путями и равновесие должно лишь уравнять суммарные прямой и обратные потоки. Однако легко видеть, что в таком случае молекула фермента окажется вечным двигателем. В равновесии при неизменных концентра­циях всех веществ в замкнутой системе молекулы фермента со­вершали бы циклические конформационные превращения и на­гревали бы среду вследствие обычных потерь на трение. В дей­ствительности термодинамическое равновесие обязательно озна­чает и детальное равновесие, т. е. равновесие на каждой элс-
ментарной стадии. В любой кинетической схеме, содержащей замкнутые циклы, условие детального равновесия накладывает связи на константы скорости (см., например, стр. 61).

Для регулирования активности фермента существенно то, что по крайней мере в одной из конформаций образование продукта происходит быстрее, чем переход между конформационными со­стояниями фермента. Возникающие нелинейные эффекты очень чувствительны к регулирующим факторам.

Изложенная теория с успехом применима, в частности, для интерпретации своеобразного кинетического поведения лактатде - гидрогеназы [64].

Неравновесные свойства ферментов весьма существенны. В ра­боте Марковича и Крапивинского [ПО] были обнаружены медлен­ные конформационные изменения фермента, продолжающиеся до 20—30 мин. Таковы конформационные изменения окружения SH-групп активного центра D-глицеральдегид-З-фосфатдегидро- геназы (ГАФД) в присутствии ингибитора — АТФ. Эти измене­ния проявляются в дифференциальных спектрах поглощения и в спектрах кругового дихроизма, в полосе поглощения специфи­ческих флуоресцентных меток. Предполагается, что малая ско­рость перестроек активного центра, индуцированных АТФ, объяс­няется их сопряжением с перестройками контактных площадок между субъединицами (ГАФД — тетрамер) и с последующими изменениями расположения субъединиц. В компактной тетрамер - ной структуре последние изменения невозможны из-за стериче - ских ограничений. Конформационный переход реализуется на промежуточной стадии димера или «рыхлого» тетрамера с по­движными контактами субъеднниц. Медленность перехода обус­ловлена низкой константой скорости диссоциации тетрамера. После перехода, вызванного АТФ, происходит ассоциация проме­жуточных форм, причем образуется тетрамер с иным расположе­нием субъединиц. Эти представления подтверждаются исследо­ваниями миграции энергии электронного возбуждения между хромофорами, расположенными на различных субъединицах. В последующих работах [111, 112] было проведено детальное из­учение кинетики ферментативных реакций ГАФД, кинетики свя­зывания ферментом АТФ и кофермента (НАД), подтвердившее изложенные представления и раскрывшее природу кооператив­ных свойств фермента, определяемых его четвертичной структу­рой и неравновесным состоянием.

Возможность весьма медленных конформационных пере­строек фермента непосредственно свидетельствует о необходи­мости учета неравновесности и нелинейности ферментативных процессов в такого рода случаях.

Рассмотренное в данном параграфе нелинейное поведение ферментов не является организованным во времени—система не может выполнять незатухающие колебания, если в ней нет автокаталитических стадий, обратных связей.

Мы видим, однако, что отдаленность от равновесия приводит к разнообразным видам регулируемого поведения биохимиче­ских систем. Можно думать, что эти возможности реализуются, в частности, в сопрягающих мембранах (см. гл. 6 и 7).