ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

АВТОКОЛЕБАНИЯ ПРИ ФОТОСИНТЕЗЕ

Периодические процессы непосредственно проявляются в фи­зиологии как животных, та'.с и растительных организмов. Речь идет прежде всего о процессах, связанных с вращением Земли вокруг ее оси, со сменой дня и ночи, таких, например, кал че­редование сна и бодрствования В связи с этим было введено понятие биологических часов [66]. Хальберг назвал циркадными ритмами биологические колебания с периодом, близким к суточ­ному [83]. Питтендрай перечисляет характерные особенности циркадных ритмов в статье [84]. Циркадные ритмы повсеместны в живой природе и имеют эндогенный и врожденный характер. Физическая причина циркадных ритмов лежит в автоколебатель­ных процессах, периоды их практически независимы от темпе­ратуры и от химических возмущений. Они автономны на клеточ­ном и организменном уровне.

Наряду с циркадными, суточными, ритмами периодических изменений состояния всего организма в живой природе наблю­дается ряд колебательных явлений с другой периодичностью, которые также следует отнести к категории биологических ча­сов. Рассмотрим в качестве примера колебания интенсивности фотосинтеза. Ясно, что фотосинтез непосредственно связан с ос­вещенностью. Скорости поглощения С02 и выделения 02 зеле­ными растениями также периодичны. По-видимому, периодич­ность, определяемая эндогенным ритмом, свойственна темповому циклу Кальвина (см. стр. 360), так как реакции светового цикла протекают очень быстро — за доли секунд. По-видимому, ритм, связанный с темновым циклом, характеризуется периодом, су­щественно меньшим суток. Однако этот ритм хорошо синхро­низуется с периодической освещенностью.

Очевидно, что непосредственно наблюдаемый ритм фотосин­теза должен определяться периодическими биохимическими про­цессами темнового цикла. Мы видели, что периоды колебаний ферментативной активности могут быть и весьма длительными. Теоретическая модель колебаний в темновых реакциях Фотосин­теза разработана Чернавским и его сотрудниками [18, 85—87].

В цикле Кальвина участвуют трехуглеродные, нятиуглерод - ные и шестиуглеродные соединения (см. рис. 7.18). Написание всех кинетических уравнений для цикла приводит к системе, слишком сложной для исследования. Как справедливо указы­вается в [18], целесообразно максимальное упрощение системы, сохраняющее, однако, ее основные качественные особенности. Кинетика процесса лимитируется медленными стадиями, быст - p&w обратимые стадии могут рассматриваться как равновесные. Поэтому следует ограничиться рассмотрением лимитирующих стадий. В сущности, такая процедура уже применялась при ана - лпзе ферментативных реакций в §§ 8.6, 8.7. Упрощение. системі кинетических уравнений проводится на строгих математических основаниях. Рассмотрим их вкратце (ар. [18]).

Имеем исходную систему типа

Xi = Fi(xu *2. xN), t = 1, 2 iV, Ш)

Допустим, что после ряда преобразований и выбора соответ-: ствующих масштабов удается расположить эту систему по сте­пеням малого параметра є при производной

Є2*, = F і (хи. . ., xN), г=1, 2, ...,/, Ї

Bx,^Fj(xu. . ., xN), j = l+\, ..., l + m, > (8.99) xk = Fk(xu. . ., xN), k = l + m+ 1, . . ., N.)

Коэффициенты є2 и є определяют скорости изменений перемен­ных х. В самом деле, систему (8.99) можно переписать. в виде

Ті Тз

Где ті = є2, т2 = є, тз = 1, т. е. ті <С т2 <С т3. Если существенно' поведение системы как на малых отрезках времени порядка ti, так и на больших порядка тз, то приходится изучать систему в целом. В других случаях ситуация иная. Так, если важны яв­ления, происходящие за средние времена порядка т2, то система' упрощается. В самом деле, за эти времена «медленные» пере­менные xh не успевают измениться, и можно заменить' их на-, чальными, постоянными значениями. Напротив, «быстрые» пе­ременные Хі успевают достичь своих стационарных значений," если таковые существуют. Значит, переменные xt можно заме­нить их стационарными значениями. Таким образом, из N урав­нений остаются лишь т уравнений.

Математическое обоснование процедуры связано с так на­зываемой теоремой Тихонова (см. [18, 113, 114]). .

Вернемся к фотосинтезу. Чернавский и сотрудники ограни­чились здесь исследованием всего лишь двух кинетических урав­нений. в которых в качестве независимых переменных фигури­руют концентрации трехуглеродных и шестиуглеродных соеди­нений С3, Сб. Остальные переменные выражаются алгебраически через С3, С6. Так как в цикле Кальвина протекают в основном бимолекулярные реакции, кинетика выражается уравнениями второго порядка

= a, q + a2c3c6 + a3c§. j (8 j00)

С^СІ + Р^ + РзС* j

В первом уравнении аз = О — концентрация триоз С3 не изме­няется в результате взаимодействия двух гексоз. Увеличение Сб может осуществляться лишь за счет соединения двух молекул Сз. Следовательно, Pi > 0, р2, Рз < 0. Увеличение содержания триоз происходит в более сложном процессе, в котором уча­ствуют как сами триозы, так и гексозы Сб - Можно положить осі > 0, аг < 0. Мы получаем уравнения

Рі^з Рг^з^б Рз^б> J

Где все коэффициенты ар, > 0.

Находим изоклины и стационарные состояния, отвечающие С3 = С6 = 0. Обе изоклины представляют собой прямые линии, проходящие через начало координат, их уравнения С6 = а[С3 и Сб — а2С3, где Я] и а2 удовлетворяют условиям а\ — а2а\ =0 и |3j — Р2а2 — рза2 = 0. Имеется лишь одно стационарное состоя­ние C° = CJ? = 0 при й\ ф а2 или бесконечное множество таких состояний при й\ — а2. Первый случай соответствует отсутствию фотосинтеза, второй — безразлично неустойчивым состояниям равновесия. Предельных циклов нет, нет и колебаний. Следо­вательно, система (8.101) недостаточна, модель требует до­стройки. Чернавский вводит в первое уравнение добавочный по­стоянный член ао > 0, описывающий скорость притока С3, воз­никающего в других процессах, отличных от цикла Кальвина (гликолиз, дыхание). Такой приток служит инициатором цикла. Необходимость пускового механизма характерна для автоката­лиза. Итак,

= а1с3 — а2с3с6 + а0' 1

J (8.102) c6=P, q-P2c3c6-P3q. J

Исследуем эту систему уравнений. Перейдем к переменным Х = С3/С°3, У = С6/С°, где С» — стационарные значения С3, Сб, получаемые из условий С3 = С6 = 0. Имеем

X = а\Х2 — a2XY а0, )

- „ - - п ( (8.103)

У = РіХ — РзХУ — Р2У, J

Где а, а2 = а2С°, а0 = а0/С°, Р, = ftC^/Cg, Э3 = Р3Со

Р2 = Р2С«. В стационарном состоянии X = Y — 1, X = Y = 0. Сле­довательно,

«і — «2 + «о = 0, 1

. . . } (8.104)

Р,-Р2-Рз = 0. )

Далее опустим черту над буквами щ и |3j. В стационарном ре­жиме коэффициент |3| представляет количество гексозы, обра­зующейся в единицу времени из триозы, |3г — количество гек­созы, уходящее из цикла Кальвина и образующее крахмал, |33 — количество гексозы, возвращающееся в цикл. Для ухода одной молекулы гексозы нужно шесть оборотов цикла, так как в цикле усваивается одна молекула СОг. Поэтому fb = Рз/6. Следовательно, р3 = 6|3i/7, |32 = |3i/7. С другой стороны, а0 «С «ь а. Имеем, вводя безразмерное время т = tjx' = a\t,

DX dx dY dx

Aj

(8.105)

Ил О2

Ai

Линеаризуем систему, рассматривая ее вблизи стационарного состояния, т. е. считая

Х=\+х, Y=l+y, х, у< 1.

Получаем из системы (8.105), исключив а2 с помощью первого соотношения (8.104),

(8.106)

Dx

Ж = (1-у)х-(\+у)у,

Dy 8 , .

Ж = тв{х-у),

16,

У7еу]'2. (8.107)

Где у = ao/ai

Є = Pi/aj. Ищем решения в виде х = х0ехр Хх, у = у0ехрХх. Находим корни характеристического уравнения К 2 = 7а (1 - Y - 8/?е) ± ['д (1 - Y - 8/7е)2 -

Стационарное состояние х = у — 0 устойчиво, если действи­тельная часть X отрицательна, т. е. если

1 — Y — 8/7е < 0.

И неустойчиво в противоположном случае.

Переход к неустойчивому режиму происходит при е = = 7/e(1 — v) ~ 0,87 (так как!)• При увеличении at такой переход оказывается возможным.

Мнимая часть (8.107) определяет колебания. Их период (без­размерный) равен

2п

Т =

ІшЛ '

15 М. В, Волькенштейн
где

1т % = ± [16/7еу - (Re Я)2]7'. При переходе к неустойчивому режиму, когда Re К

Dy _ 2 *2 - Ч? у2 - ehxy dx З X2 — 21І20ХУ + V20 '

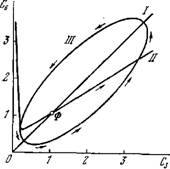
Рис. 8.35. Фазовый портрет для

Модели фотосинтеза [84]. i и ii—линии параллельных и пер­пендикулярных изоклин, iii—пре­дельный цикл. Ф(Х = У = 1) — устой­чивый фокус.

2л

Т =

Vl6/7eY

Поведение системы исследуется обычным методом «фазовых диа­грамм. Положим для конкретности y ^ 1/20 и е » 2/3. Тогда

Условие неустойчивости соблюдает­ся, так как

16

21 '

Интегральные кривые представля­ются уравнением

(8.108)

На рис. 8.35 показан фазовый порт­рет системы уравнений (8.106) при указанных значениях у и е. Систе­ма является автоколебательной, Сз и С6 периодически изменяются с одинаковой фазой. Численное или графическое определение периода колебаний С3 и С6 показывает, что он примерно на два порядка больше характеристического времени т'-^-а"1. Это время оце­нивается в 5—10 мин, период Т порядка нескольких часов или суток. Колебания ангармоничны: система проводит боль­шую часть времени в области малых значений концентраций С3 и С6.

Машинные расчеты показывают, что система синхронизуется внешним периодическим воздействием (освещенность). При пе­реходе от одного режима к другому фаза устанавливается мед­ленно.

Более подробное исследование системы уравнений (8.106) выполнено в работе [87] (см. также [18]).

О, имеем

Очевидно, что приведенное рассмотрение максимально упро­щенно и не позволяет еще сделать какие-либо количественные выводы. Однако упрощенный подход раскрывает физический смысл автоколебаний при фотосинтезе и показывает, как они могут синхронизоваться суточным ритмом.