ЖЕЛЕЗОБЕТОННЫЕ ДЕТАЛИ МАШИН

ОБЩИЕ ПОЛОЖЕНИЯ РАСЧЕТА

На железобетонные базовые детали машин в общем случае действуют статические и динамические нагрузки: вес узлов машин и обрабатываемых деталей; составляющие силы резания, усилия прокатки, штамповки и ковки; крутящие моменты двигателей; инерционные силы от поступательного движения и вращения масс и т. п.

По возможным схемам расчета базовые железобетонные де­тали можно разделить на следующие группы: брусья (станины, стойки); рамы (портальные станины, рамы транспортных машин, фундаментные рамы); пластины (плиты, планшайбы, столы); штампы (шаботы молотов) и прочие (цилиндры, плунжеры, толстые плиты и т. п.).

Под воздействием нагрузок железобетонные детали могут на­ходиться в сложном напряженном состоянии, составляющем ком­бинацию основных его видов (внецентренное растяжение и сжатие, изгиб, кручение).

Статический расчет (определение внутренних усилий) железо­бетонных деталей производится методами строительной механики стержневых систем. Однако использование железобетона для изго­товления деталей машин в ряде случаев вызывает появление новых конструктивных решений и форм элементов, для которых пока не разработаны методы статического расчета. Для массивных элементов в ряде случаев на смену методам строительной механики стержневых систем приходят методы теории упругости. Ведутся теоретические исследования работы массивных элементов и разра­ботаны практические методы расчета цилиндрических архитравов, массивных железобетонных рам, составленных из прямоугольных элементов, и других деталей [28].

Базовые несущие системы машин должны обеспечивать и со­хранять в течение длительного срока службы правильное располо­жение и возможность точных перемещений узлов, инструмента и изделий. В ряде машин и станков не только остаточные, а даже небольшие упругие деформации деталей могут привести к не­правильной работе системы. Поэтому основным критерием работо­способности базовых деталей является их жесткость, которая определяется собственными деформациями несущих систем и мест­ными деформациями в сопряжениях [16].

В связи с этим основными требованиями, предъявляемыми к железобетону при его применении в конструкциях большинства машин, является: обеспечение неизменяемости во времени перво­начальных геометрических размеров элементов машин и повыше­ние их жесткости при распределенных и местных нагрузках.

Базовые детали в машинах являются наиболее сложными и трудоемкими. Поломка корпусной детали надолго выводит всю машину из строя, поэтому размеры их сечений должны удовлетво­рять требованиям прочности при воздействии наибольших, воз­можных в условиях эксплуатации, нагрузок. Если для металли­ческих корпусных деталей расчет на прочность не является обяза­тельным (кроме сильно нагруженных деталей), а в ряде случаев прочность автоматически удовлетворяется расчетом на жесткость (малонагруженные станины металлорежущих станков, плиты и т. п.), то в железобетонных деталях напряжения могут вызвать появление трещин в растянутой зоне вследствие низкого сопро­тивления бетона на растяжение. Поэтому необходимые размеры сечений железобетонных элементов всегда назначаются по усло­виям прочности от статической нагрузки.

При воздействии динамических многократноловторных на­грузок возможны усталостные разрушения, поэтому железобе­тонные элементы деталей надо рассчитывать в этом случае по пре­делу выносливости бетона и арматуры. Расчет на выносливость дополняет, но не заменяет расчета на прочность. Размеры сечений элементов выбирают по наиболее неблагоприятным данным, полу­ченным из расчета на прочность и выносливость.

При расчете несущих элементов машин малой динамичности (большинство металлорежущих станков) динамические нагрузки можно не учитывать [42 ]. Для машин средней и большой динамич­ности расчет конструкций на прочность и выносливость произво­дится с учетом коэффициента динамичности.

Надежность и точность работы машин зависят не только от общей прочности и жесткости несущих деталей, но также и от прочности и жесткости крепления закладных металлических дета­лей в железобетоне. Поэтому такой расчет является важным и не­обходимым. Способы расчета прочности и жесткости анкеровки металлических закладных деталей в бетоне при различных сило­вых воздействиях разрабатывают на основе экспериментальных исследований, с учетом многочисленных факторов, влияющих на работу анкеровки деталей.

Разработка общей методики расчета железобетонных базовых деталей машин встречает ряд трудностей из-за: принятого в ма­шиностроении чисто индивидуального подхода к проектированию деталей; отсутствия нормативного материала по расчету (лими­тирующие деформации, коэффициенты условий эксплуатации, коэффициенты перегрузки и т. п.); сложности статического рас­чета в связи со сложностью форм. Для решения этих вопросов требуются широкие теоретические, экспериментальные и стати­стические исследования.

РАСЧЕТ НА ПРОЧНОСТЬ

Выбор методов расчета. Для расчета строительных железобетон­ных конструкций'в СССР в настоящее время принят прогрессивный и эффективный метод расчета по предельным состояниям, который приводит к более экономичным конструкциям,

Применение железобетона в машиностроении вызывает необ­ходимость учитывать ряд особенностей, присущих деталям машин.

Так, например, для большинства железобетонных деталей машин и станков трещины в растянутой зоне недопустимы.

Если в конструкции появляются трещины, то полное сечение бетона будет ими ослаблено. По мере раскрытия трещин момент инерции сечения уменьшается, следовательно, прогиб будет на­растать. Таким образом, сечение с трещинами имеет меньший момент инерции, а следовательно, меньшую жесткость и боль­шие прогибы. Это неблагоприятно сказывается на работе деталей машин, критерием работоспособности которых является же­сткость.

Трещины нарушают сцепление арматуры с бетоном, а также способствуют коррозии арматуры и бетона вследствие свободного доступа через них влаги и агрессивных сред (масел, эмульсий и т. п.). Трещины понижают жесткость и долговечность железо­бетонных конструкций.

Размеры элементов базовых деталей машин предопределяются условиями жесткости, длительного сохранения высокой точности геометрических размеров. В большинстве машин нельзя допускать, чтобы отдельные детали имели остаточные деформации и работали за пределами упругости [26]. В процессе эксплуатации деформа­ции деталей всегда упругие. В противном случае при остаточных деформациях машины фактически вышли бы из строя. Отсюда следует, что элементы железобетонных базовых деталей машин работают обычно в I (упругой) стадии, с напряжениями в сечениях, не превышающими определенных величин допускаемых напряже­ний. Поэтому наиболее приемлемым для расчета элементов железо­бетонных деталей машин является расчет по упругой стадии, по формулам сопротивления материалов с учетом свойств железо­бетона [15, 32, 37].

Если в сечениях элементов железобетонных деталей машин возникают растягивающие напряжения, не превосходящие до­пускаемых, они легко воспринимаются обычным железобетоном.

Силовые же рамы и другие сильно растянутые и изгибаемые элементы необходимо изготавливать из предварительно напряжен­ного железобетона.

Использование для железобетонных деталей машин высоко­прочных однородных бетонов высокого качества дает возможность учитывать его работу на растяжение до величин допускаемых на­пряжений.

В настоящей главе рассматриваются вопросы статической прочности элементов деталей машин из обычного железобетона.

Допускаемые напряжения и коэффициенты запаса. Выбор допускаемых напряжений является очень важным и наиболее ответственным этапом в расчетах деталей машин на прочность. В практике расчетов J деталей на прочность известно _несколько 2 А.

Методов выбора допускаемых напряжений. Для расчета на проч­ность железобетонных деталей машин, учитывая ответственность их, целесообразно воспользоваться наиболее современным и про­грессивным методом — дифференциальным или методом частных коэффициентов [22 ].

В общем случае формула для расчета допускаемых напряжений имеет вид

Предельные напряжения

Допускаемые напряжения = —--------------------------------------- .

^ ґ запас прочности

Прочность деталей характеризуется предельными напряже­ниями. При статическом нагружении деталей для хрупких мате­риалов (чугун, твердые стали, бетон) характеристикой прочности является предел прочности, для пластичных (мягкие стали)— предел текучести. Пределы прочности бетона для основных видов напряженного состояния (призменная прочность сжатие

При изгибе R", растяжение Rp) определяются в зависимости от марки бетона (см. табл. 1). Для горячекатаной арматуры, контро­лируемой характеристикой прочности, является браковочный ми­нимум предела текучести, для холоднообработанной арматуры — браковочный минимум предела прочности. В табл. 4 [40] приве­дены нормативные сопротивления R% (браковочные минимумы пределов прочности и текучести) арматуры всех классов.

Выбор коэффициента запаса прочности в основном зависит от наличия концентраторов напряжений, однородности материала детали, степени ответственности детали, точности расчета и харак­тера нагрузок.

Концентрация напряжений. В местах острых углов, отверстий, подрезов, неплавных сопряжений и т. д. при нагружении детали возникают местные повышенные напряжения, называемые «кон­центрацией напряжений».

При статическом нагружении концентрацию напряжений в же­лезобетоне можно не учитывать.

Концентрация напряжений опасна при динамическом нагруже­нии деталей, но и здесь наблюдается сглаживание напряжений за счет пластической податливости материала. В этом случае в расчет вводят действительные коэффициенты концентрации напряжений k0 и kx, которые определяются экспериментально.

Однородность материала деталей. Прочность материалов обла­дает изменчивостью. При испытании образцов одной и той же партии материала наблюдается естественный разброс. Изменчи­вость прочности зависит от характера самого материала и совер­шенства технологического процесса его изготовления и устана­вливается опытным путем на основании многочисленных наблю­дений.

Путем испытания партии образцов получают среднее значение прочности материала R. 18

Пониженная прочность $min принимается за возможный прё - дел снижения прочности материала (бетона и арматуры) в практи­ческих условиях. Учитывая, что при расчете по допускаемым на­пряжениям применяется общий коэффициент запаса, состоящий из ряда частных, вводится коэффициент изменчивости механи­ческих свойств материалов kU3 по величине, обратный коэффи­циенту однородности k°6 и k°a, принятому в СН и П*.

Коэффициент изменчивости механических свойств материала

Рекомендуется принимать коэффициенты изменчивости свойств материала, полученные на основании практики эксплуатации железобетонных конструкций, а также статистических данных контрольных испытаний [37].

Для высокопрочных бетонов марок 300—700 сжатие осевое и при изгибе k6U3c = 1,70; растяжение, срез, скалывание k6U3p = 2,0.

Для арматуры из горячекатаной стали класса А—I (марок Ст. 0 и Ст. 3), а также для арматуры из Ст. 0 и Ст. 3, подвергнутой силовой калибровке, kaU3= 1,1.

Для арматуры из горячекатаной стали периодического профиля класса А—II и А—III (Ст. 5 и 25Г2С) kaU3 = 1,2.

Для холодносплющенной арматуры периодического профиля и для арматуры из холоднотянутой проволоки kaU3 = 1,25.

Довольно низкие коэффициенты изменчивости механических свойств для арматуры объясняются тем, что они назначены по отношению к браковочному минимуму прочностных характеристик, а не к средним характеристикам.

Степень ответственности детали. Степень опасности разруше­ния детали оценивается коэффициентом ответственности детали kom, который назначается в каждом конкретном случае [22]. Реко­мендуется принимать следующие величины коэффициента ответ­ственности деталей, когда выход из строя детали: не вызывает остановки машины kom = 1; вызывает остановку машины kom — 1,1 - г-1,2; вызывает аварию kom = 1,2-^1,3.

Точность расчета. Расчет железобетонных базовых деталей машин со сложными расчетными схемами, сечениями и характером загружения требует многих допущений и упрощений. Относитель­ная точность расчета в связи с упрощением схем загружения дета­лей, упрощенным пониманием условий работы детали, усреднением расчетных данных и т. п. оценивается коэффициентом точно-

* Коэффициент k6U3 —------ — и fe°3 =—— принят для удобства его исполь-

Зования в формуле (2). 20

Cl-и расчета km р. Ориентировочно можнб принимать km „ — = 1,1-5-1,3 [22].

Характер нагрузок. Вводимые в расчетные формулы нагрузки назначаются на основании экспериментально-теоретических и статистических данных о работе деталей.

Действующие на детали внешние нагрузки можно подразде­лять на нормативные и расчетные. За нормативные принимают •максимальные нагрузки, соответствующие нормальным условиям эксплуатации машин. За расчетные принимают наибольшие на­грузки, возможные в условиях эксплуатации, вследствие случай­ных перегрузок.

Превышение расчетной нагрузки по сравнению с нормативной оценивается коэффициентами перегрузки kn, которые устанавли­вают на основании опыта проектирования, эксплуатации машин и статистической обработки результатов длительных наблюдений.

Аналогично частными коэффициентами можно оценивать и дру­гие факторы, влияющие на выбор прочности в каждом конкретном случае.

Произведение частных коэффициентов называют коэффициентом запаса прочности материала детали:

^ = ^из^от^т. Pknt (2)

Тогда допускаемые напряжения равны

^ ___ предел прочности ^

Необходимо отметить, что допускаемые напряжения для бе­тона не должны превышать предела упругой работы бетонов, который в 2,5—3,5 раза ниже марочной (кубиковой) прочности или 0,4RnP. При таких напряжениях модули упругости на сжа­тие и растяжение приближенно можно считать постоянными и равными начальному модулю упругости Еб.

При напряжениях, превышающих указанные пределы, модули упругости снижаются из-за появления пластических деформаций, и в элементах возникают остаточные деформации.

Для железобетонных элементов характерно, что коэффициенты запаса прочности сжатого бетона (k6_c), растянутого, бетона

РУ и Для арматуры (ka) будут иметь различные значения.

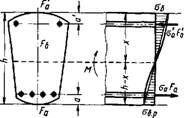
Осевое сжатие. К центрально-сжатым элементам относятся стойки, штампы и т. п. По конструкции железобетонные стойки можно разделить на следующие основные типы: стойки с гибкой продольной арматурой и хомутами; стойки с косвенной арматурой в виде спиралей или сварных колец, т. е. бетон в обойме и стойки с жесткой арматурой.

При расчете основываются на следующих допущениях: напря­жения сжатия распределяются равномерно по всему сечению; вследствие надежного сцепления арматуры с бетоном железобе­тонный стержень будет работать как одно целое и деформации

Арматуры и бетона будут равны; модуль упругости бетона при напряжениях, не превышающих допустимых, постоянен и равен начальному модулю упругости.

Напряжения в бетоне определяют по формуле

N

Об = - г~< \Об. пр], (4)

' пр

Где N — сжимающая продольная сила;

Fnp = F6 + nFa — приведенная к бетону площадь сечения элемента; Fa и F6 — соответственно площади сечения арматуры

(металла) и бетона сжатого железобетонного элемента; п =

£

= ----------- коэффициент приведения:

£■6

RH

[°б. яр] = пг^--------- допускаемое напряжение бетона на сжатие.

С

Напряжения в арматуре определяют по формуле

NN_ *пр

RH

Где [оа] = — допускаемое напряжение арматуры на сжатие.

Расчетные формулы для определения размеров поперечного сечения стойки выразятся следующим образом:

TOC \o "1-3" \h \z?6 = [Об. пр] (1 (6)

Fa = vF6, (7)

Где [л — коэффициент армирования.

Осевое растяжение. Допускаемое растягивающее усилие равно

N = [a6.p\(F6 + nFa). (8)

Напряжения растяжения в бетоне определяются по формуле

И 1 ПР

Площадь сечения бетона и арматуры рассчитывают по фор­мулам:

Р6= \об. р](\+п»)' (10)

Где

Fa = VF6. (11)

Изгиб. Все однородные тела на изгиб рассчитывают на осно­вании следующих допущений: соседние волокна не оказывают 22
друг на друга влияния; удлинения пропорциональны напряже­ниям (закон Гука); модуль упругости для всех волокон постоян­ный и не зависит от знака напряжений; плоское сечение при из­гибе остается плоским (закон Бернулли).

Для железобетона из этих допущений принимают только закон Бернулли. Сечение железобетонной балки при изгибе остается плоским, поэтому изменения длины волокон прямо пропорциональны расстояниям этих волокон от нейтральной оси.

Так как для бетона не совсем справедлив закон Гука и зави­симость между деформациями и напряжениями имеет нелиней­ный характер, то последние распределяются в сечении по кривой. При малых напряжениях эта кривизна незначительная и модуль упругости бетона при растяжении и сжатии почти одинаковый. Поэтому без особой погрешности эпюра напряжений в сечении может быть принята прямолинейной (закон Гу­ка). При таких предположениях напряжения в железобетоне рас­считывают по общим законам соп­ротивления материалов так же, как и балки из однородного мате­риала, причем различие модулей упругости стали и бетона учиты­вается заменой сечения стали п-кратным сечением бетона.

Для сечения любой симметричной формы (рис. 7) выражения напряжений в бетоне и арматуре будут иметь вид

М /г л

Об = - і— X < [об. J;

' пр

Об. р =

(h — х) < [Об. р.«]; оа=п - г— (h — x — a)< [oj Оа = П - р - (х — а) < [о J,

Где J

Пр

Приведенный к бетону момент инерции относительно нейтральной оси (центра тяжести сечения). Положение нейтральной оси определяется из условия

Sno (16)

Зпр спр

В выражениях (12), (13) и (14), (15) допускаемые напряжения определяют следующим образом:

Допускаемое напряжение бетона на сжатие при изгибе

К

Допускаемое напряжение арматуры

К

Допускаемое напряжение бетона на растяжение при изгибе

Rн

Sp. и

[Об.,

■Р-и>- кб. р ■

Величина Rp. u не обусловлена строительными нормами. Но, как показали опыты проф. Б. Г. Скрамтаева, предел прочности бетона на растяжение при изгибе Rp. и у растянутого края бетон­ной балки, вычисленный по обычной формуле изгиба Rp. и = = в 1,7 раза больше предела прочности Rнр при осевом растя­жении, согласно нормам.

Поэтому допускаемые напряжения бетона на растяжение при изгибе целесообразно выразить через RHp-.

Практически из приведенных выше величин напряжений важно учесть лишь растягивающее напряжение, поскольку бетон имеет низкий предел прочности при растяжении.

Если удовлетворяется условие (13), все остальные условия выполняются автоматически, поэтому проверку об, ва, оа можно и не делать.

Допустимый изгибающий момент по растянутой зоне опреде­лится по формуле

Для прямоугольного сечения с двойной арматурой, имеющего высоту h и ширину Ь\

Sap = + nFa (h — а) + nFaa'; (19)

Fnp = bh-\- hFa - f nF'a, (20)

Jnp =№. + nFa(h — x — af + nF'a (x - a')2 + b{h~x)S (21)

Значения Fnp, Snp и J подставляют в формулы (12, 13, 14, 15, 16 и 18). 24

Таким же образом опреДбляюї напряжения Для сечений любой сложной конфигурации.

При расчете сечений с одиночной арматурой, расположенной в растянутой зоне, из всех формул выпадает значение Fa = 0.

Расчет на скалывание при изгибе. Если рассматривать работу железобетонной балки в I стадии (с учетом работы растянутой зоны бетона), то картина распределения главных напряжений будет приблизительно соответствовать случаю однородной балки.

Железобетонные балки в отличие от балок tH3 однородного материала разрушаются не только в середине пролета, а и у опор. Там образуются наклонные трещины из-за больших главных растягивающих напряжений.

Происходит это потому, что сопротивление бетона скалыва­нию RcK колеблется в пределах 42—70 кГ1см% и значительно превос­ходит сопротивление его растяжению (R" в пределах 21—35 кГ/см2). Разрушение идет по линии наименьшего сопротивления, т. е. трещины образуются по направлениям, перпендикулярным к траекториям главных растягивающих напряжений. Поэтому для железобетонных балок главные растягивающие напряжения гораздо опасней скалывающих, и проверку на скалывание нужно заменить проверкой главных растягивающих напряжений. Наибо­лее опасны сечения, в которых направления главных растяги­вающих напряжений значительно отличаются от направления растянутой арматуры, при величине этих напряжений, мало отли­чающихся от максимума. Это сечения, лежащие в растянутой зоне вблизи нейтральной плоскости. Так как нормальные напряже­ния в них невелики, то главные растягивающие напряжения по численному значению близки к скалывающим. Приближенно можно принять, что вблизи нейтральной оси в растянутой зоне

®гл. р ^max•

Во избежание образования в железобетонных балках наклон­ных трещин необходимо, чтобы главные растягивающие напряже­ния огл. р не превосходили временного сопротивления бетона на растяжение Rp. Если по расчету огл, р >> Rp, то сечение балки необходимо увеличить. При агЛш р < [об. р] главные растяги­вающие напряжения могут быть надежно восприняты бетоном без дополнительного специального армирования.

Внецентренное сжатие. Если от внецентренного сжатия в по­перечном сечении железобетонного элемента возникают или только напряжения сжатия, или с одной стороны — сжатия, а с другой, не превышающие допускаемых, напряжения растяже­ния, которые не могут вызвать появление трещин, расчет ведется по одному методу с учетом работы всего сечения.

Особо рассматривается случай, когда растягивающие напряже­ния достигают значительной величины. При этом обычный желе­зобетон, как правило, заменяют предварительно напряженным.

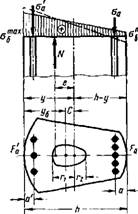
Для сечения любой формы (рис. 8) напряжения определяют по следующим расчетным формулам:

N

< [об.«];

"пр

Min N

Об = - в—

Г пр

] < [оа];

Гпр

N__ Ne0(h-y-a)

Рпр J пр

Приведенная площадь железобетонного сечения слагается из площади бетона и л-кратной площади арматуры;

FnP=F6 + n(Fa + F'a). (26)

Положение центра тяжести находят по формуле

РбУб + пРа (h—a)+nFa p6 + n(Fa + K)

Пр

Приведенный момент инерции сече­ния относительно его центра тяжести равен

Jnp Jfj F6c2 nFa (h — y — af +

NFa (h — a )2,

Определим координаты наиболее уда­ленных точек контура ядра приведен­ного сечения. Если нормальная сила N будет приложена на контуре ядра сечения, а изгибающий момент М = Nrlt то напряжение бетона у менее сжатого края сечения будет равно нулю, т е.

Об1 «= « - = о, (29)

'пр

Откуда

'пр

Fnp(h-y) '

РпрУ

Внецентренное растяжение. К внецентренно растянутым элемен­там относятся стойки сверлильных, фрезерных станков, прокат­ных станов, листоправйльных машин и другие корпусные детали.

Обычный железобетон плохо работает на растяжение, поэтому приведенные выше конструкции, как правило, выполняются из предварительно напряженного железобетона.

Если продольная сила N приложена внутри ядра сечения и растягивающие напряжения в бетоне не превышают допускаемых, то расчет сечения при внецентренном растяжении производится как при внецентренном сжатии, с учетом работы бетона на растя­жение. При этом значения внешней силы и эксцентриситета бе­рутся с обратными 'знаками. Если напряжения в бетоне от вне - центренного растяжения превышают допускаемые напряжения, то в этом случае переходят на напряженный железобетон.

Кручение. Явление кручения в железобетонных деталях ма­шин имеет место во многих случаях. Обычно кручение наблю­дается с изгибом.

Наклонные трещины в бетоне появляются от действия главных растягивающих напряжений по траекториям, пересекающим тре­щины под углом 90°. В практике элементы, работающие на кру­чение, армируют продольной арматурой и вертикальными зам­кнутыми, часто расположенными хомутами (кольцами).

Наружный слой бетона, прикрывающий продольную арматуру, в расчет не вводят. Сопротивление кручению складывается из сопротивления бетона и поперечной арматуры.

Если вычисленные наибольшие главные растягивающие на­пряжения бетона не превосходят допускаемых [об. р], то спе­циального армирования не требуется.

Если же главные растягивающие напряжения превышают допускаемые, то элемент нужно армировать специальной армату­рой с направлением витков, совпадающим с направлением круче­ния или продольной арматурой, охваченной замкнутыми хому­тами.

Наибольшую величину главных растягивающих напряжений

H

Для прямоугольного сечения при обычных отношениях — =

1,5-ьЗ можно вычислить по формуле

М,

Если огл.£>> [об р], то в расчет вводят сечение хомутов и продольной арматуры. Площадь сечения одного хомута опре­деляют по формуле

2К16А *

Где а — расстояние между хомутами;

Ья и Ня — размеры ядра сечения.

При наличии в элементе дополнительной продольной арматуры с сечением стержня при расстоянии между стержнями а, сече­ние стержня будет

<34>

Особенности расчета составных сечений. Составные сечения состоят из нескольких материалов. Так, в железобетонных дета­лях машин применяют железобетонные элементы, в сечении кото­рых значительную роль занимают металлические детали, распро­страняющиеся на часть или полную длину элементов.

Ряд исследований (экспериментальных и теоретических) дока­зывают возможность осуществления прочного и жесткого сопря­жения таких металлических деталей с бетоном при соответству­ющей их анкеровке.

При расчете элементов железобетонных деталей в упругой стадии на изгиб, центральное и внецентренное сжатие и растяже­ние можно считать совместную работу металлических закладных деталей с бетоном обеспеченной.

Приведенный выше метод расчета железобетонных элементов на прочность по упругой стадии (классическая теория) вполне пригоден для расчетов составных сечений железобетонных эле­ментов. Площадь сечения металла заменяют n-кратной площадью

Бетона п = ЕрШ ■ и в расчетные формулы добавляют элементы, б

Содержащие сечение металла закладных деталей.

Приводить подробный расчет таких сечений нет смысла, так как он аналогичен уже рассмотренному методу расчета.

Некоторые особенности приобретает расчет составных сечений при изгибе железобетонных элементов, в которых основная масса металла сосредоточена в сжатой зоне.

Концентрация металла в сжатой зоне железобетонных изги­баемых элементов ухудшает работу растянутой зоны бетона, так как нейтральная ось резко поднимается к сжатой грани сече­ния, вовлекая тем самым большую часть бетона в растянутую зону. Для уравновешивания больших площадей металла сжатой зоны требуется значительное количество арматурной стали, рас­полагаемой в растянутой зоне (при условии сохранения положе­ния нейтральной оси).