Железобетон

ПЕРЕМЕЩЕНИЯ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ

Общие положения расчета

Расчет перемещений железобетонных элементов — прогибов и углов поворота — связан с определением кривизны оси при изгибе или с определением жесткости элементов. По длине железобетонного элемента в зави­симости от вида нагрузки и характера напряженного состояния могут быть участки без трещин (или участки, где трещины закрыты) и участки, где в растянутой зоне есть трещины. Считается, что элементы или участки эле­ментов не имеют трещин в растянутой зоне, если при действии постоянных, длительных и кратковременных нагрузок с коэффициентом надежности по нагрузке = = 1 трещины не образуются.

Кривизна оси при изгибе и жесткость железобетонных элементов на участках без трещин

Кривизну оси изгибаемых и внецентренно загруженных железобетонных элементов на участках, где не образуют­ся трещины, определяют как для сплошного приведенно­го сечения в стадии I напряженно-деформированного со­стояния по формуле

L/R = M<P/B, (VII. 111)

Где М — изгибающий момент от нагрузок, для которых определяется кривизна; В — жесткоеА приведенного сечеиия, которая для тяже­лого бетона и бетона на крупном пористом заполнителе и кварцевом песке при кратковременном действии нагрузки

Ј = 0,85ЈbW (VII. 112)

І коэффициентом 0,85 учитывается снижение жесткости под влияни - ; ем неупругих деформаций в бетоне растянутой зоны; <р — коэффн - ; циеит, учитывающий снижение жесткости (увеличение кривизны) при длительном действии нагрузки под влиянием ползучести бетона ежа - ■ той зоны; при средней относительной влажности воздуха выше 40 % ои равен 2; при средней относительной влажности воздуха 40 % и ниже — 3.

Кривизну оси, вызванную выгибом 1 /г от кратковре­менного действия усилия предварительного обжатия, также определяют по формуле (VII.111) при значении изгибающего момента

М = РеаР. (VII. 113)

, Кривизну оси, вызванную выгибом под влиянием пол - Ч6учести бетона от усилия предварительного обжатия, принимают равной тангенсу угла наклона эпюры дефор­маций по формуле

1 /Г=(*Ь-ВЬ)/Н0; (VII. 114)

Здесь еь и е4— деформации бетона, вызванные ползучестью, на уров­не центра тяжести растянутой арматуры и крайнего сжатого волокна бетона; потери ас = Об+09 <хс=а6+а9;

Е. = е = A IE • el = А'/Е . (VII. 115)

B SC С S' ° с s* v '

Если трещины в растянутой зоне, нормальные к оси элемента, при действии рассматриваемой нагрузки за­крыты, то кривизны, определяемые по формуле (VII. 111), увеличиваются на 20 %.

3. Кривизна оси при изгибе и жесткость железобетонных элементов на участках с трещинами

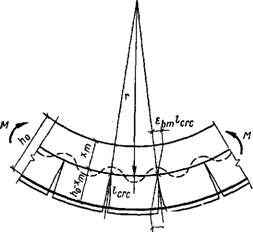
На участках, где образуются нормальные к продоль­ной оси элемента трещины в стадии II, общее деформи­рованное состояние определяют средними деформациями растянутой арматуры esm, средними деформациями бето­на сжатой зоны гьт и средним положением нейтральной оси с радиусом кривизны г (рис. VII. 14). Рассмотрим железобетонный элемент в зоне чистого изгиба. Кривиз­на оси и средние деформации арматуры и бетона связа­ны зависимостью

Icrc ESm Icrc &bmlcrc (em ~4~ e6m) Urc ,

241

Г Ло % XM После сокращения на /сгс кривизна оси при изгибе пред-

16—943
ставляется как тангенс угла наклона на эпюре средних деформаций

_1 &8тп &Bm Icrc Bgm ~Ь еьт

Г Л0 — хт Хт Ha

Принимая во внимание, что

(VIIЛ16)

<W = ^S 0S/ES; ГЪт = г|)ь оь11ь Еь, Кривизна оси при изгибе

•sm

1 _ _ %Оъ

R Es(H0 — хт) %ь Еь хт Es Л0

Рис. VII.14. К определению кривизны оси прн изгибе элемента

О з + ^FcPb ^ь Еь Іц

(VII. 117)

ЕЪт /

LSMl Ого

После подстановки в выражение (VII.117) значений на­пряжений в арматуре и бетоне Os=M/Ws, ab=M/Wc получим выражение для кривизны

Г EsWs(K-*M) HEbWcxm H0 ESWS + Xb EbWc)'

(VII. 118)

Знаменатель в выражении (VII.118) представляет со­бой жесткость железобетонного сечения при изгибе, вы­раженную или по растянутой зоне

B = (Es/^s)Ws(Aa-xm), (VII. 119)

Шли по сжатой зоне

I B = (VII. 120)

|іли по обеим зонам сечения

І ' + <™л21)

Выражения кривизны и жесткости с учетом значений ^пругопластических моментов сопротивления Ws, Wc принимают вид

І — = —Г —+ S6 1; (VII. 122)

; ' vі (ф/+|)хь ЕЬьк,

В общем случае для предварительно напряженных изгибаемых, внецентренно сжатых и внецентренно растя­нутых элементов при ho систему внешних сил и усилия предварительного обжатия заменяют эквивалент­ной системой с моментом Ms и суммарной продольной силой Ntot. Тогда напряжение в бетоне сжатой зоны, со­гласно (VII.97),

Аь = М3/Аь Гі, где Ль = (ф/ +1) Bh0; (VII. 124)

Напряжение в растянутой арматуре, согласно (VII.100), Oa^MJAspZi-Niot/Asp. (VII. 124а)

Общее выражение кривизны оси при изгибе после под­становки значений напряжений в бетоне сжатой зоны и растянутой арматуре принимает вид

— = f-^- + ^hrl - Niot * . (VII. 125) Г Vi L EsAs h Еъ Аь J h0 Ea As

Кривизна оси при изгибе I/г и жесткость В на участ­ках элементов с трещинами с течением времени изменя­ются, и поэтому в расчетах их определяют с учетом ряда физических факторов: работы бетона на растяжение на участках между трещинами, характеризуемой коэффици­ентом ij)s, неравномерности деформаций бетона сжатой зоны на участках между трещинами, характеризуемой коэффициентом - фь, неупругих деформаций бетона сжа­той зоны, характеризуемых коэффициентом Хь.

Значения

I|3s и Хь определяют с учетом длительности действия нагрузки.

16*

243

Значения коэффициента кь установлены нормами для
тяжелых бетонов и б<ет0%в на пористых заполнителях в зависимости от хараК^теР* Действующей нагрузки и усло­вия эксплуатации конструкции. При кратковременном действии нагрузки ДО—W ПРИ Длительном действии нагрузки - в условиях ересей относительной влажности воздуха выше 40 % Л/^0',15- в условиях средней относи­тельной влажности вРздУ*а 40 % и ниже Ль=0,1. Обра - тим внимание что у^тан^лены собственно значения не коэффициентов Кь, а ^нач^ия произведений соЯь, которые при принятой для 1>асч^а в стадии II прямоугольной эпюры напряжений в бет(^е сжатой зоны с коэффициен­том полноты и = 1 чгісле¥° Равны значениям кь.

4. Перемещения желё30б«10нных элементов

Прогиб Железобетонньі? с Элементов, не имеющих трв' щин в растянутых зоРах> Определяют по жесткости при­веденного сечения В и с учетом значений коэффициента <р при длительном д<гистЕііи нагрузки. Полное значение прогиба

/ = F«H,T + Jit - Fcv ~ Fcsc (VII. 126)

Где Uht- прогиб от кратковРЧ'енн°й нагрузки; /„-прогиб от по- стояннЬй и длительно дей(твУю>іІИХ нагрузок; выгиб от кратко­

Временного действия усил«я предварительного обжатия Р с учетом всех потерь; /„с-выгиб вслеДСтвие ползучести бетона от обжатия.

Выгиб предварите/115110 напряженных элементов по­стоянной высоты, выэван1^й внецентренным обжатием: F,P = Be<,Pl2/8B. (VII. 127)

Выгиб предварите-яЬН0 напряженных элементов по­стоянной высоты, выэван1^й ползучестью бетона от об­жатия: . ,2

(VII. 128)

" RCsc О

Прогиб Железобет? ННЬіС Элементов, имеющих трещи­ны в растянутых зонаОпределяют по кривизне оси при изгибе,

Ft= (*) Dx, (VII. 129)

О

Где Ж-изгибающий мом<нт в Сечеиии * от единичной силы, прило­женной по направлению iKom«° перемещения; — (*) определяют по формуле (VII.125). 244

T

; При определении перемещений железобетонных эле­ментов постоянного сечения допускается на каждом уча­стке, в пределах которого изгибающий момент не меня­ет знака, вычислять кривизну для наиболее напряженно - то сечения и далее принимать изменяющейся прямо пропорционально эпюре изгибающих моментов. Это '.допущение равносильно тому, что жесткость В вычисля­ют для наиболее напряженного сечения и далее принн - мают постоянной.

Для предварительно напряженных элементов, к ко­торым предъявляются требования 2-й и 3-й категорий по трещиностойкости, такие допущения в ряде случаев при­водят к существенному завышению прогиба против дей­ствительного значения, так как участки с трещинами в растянутой зоне могут иметь ограниченную протяжен­ность. В таких случаях прогиб

/ = 2 j мД- (х) Dx, (VII. 130)

При этом эпюру кривизны — (х) ПО длине пролета желе­зобетонного элемента разбивают на несколько участков в виде кусочно-линейной функции и вычисляют интеграл перемещений перемножением эпюр, пользуясь правилом

Верещагина. Кривизну—(л;) на каждом участке без тре­щин и с трещинами определяют по формулам (VII.111), (VII.125).

Углы поворота железобетонных элементов также оп­ределяют интегрированием по (VII.129) или (VII.130), но по моменту М в сечении х от единичного момента.

В простейших случаях прогиб изгибаемых элементов без предварительного напряжения — плит, панелей, ба­лок и т. п. — от равномерно распределенной нагрузки / = (5/384) (ql*/B).

Прогиб однопролетных балок и консолей от различ­ных нагрузок определяют по кривизне или по жесткости в сеченин с максимальным моментом по общей формуле F—Sfi (1/г) или F = SP(M/B); (VII.131)

Коэффициент s зависит от расчетной схемы элемента и вида нагрузки. Для свободно опертой балки: при равно­мерно распределенной нагрузке s = 5/48, при сосредото­ченном грузе в середине пролета s = 1/12, при двух рав­
ных моментах по концам s== 1/8; для консольной балки: при равномерно распределенной нагрузке s=l/4, при со­средоточенном грузе на свободном конце s = l/3, при моменте на свободном конце s = 1/2.

При двузначной эпюре напряжений в неразрезных балках для каждого участка жесткость принимают по­стоянной по сечению с максимальным моментом (

Прогиб коротких изгибаемых элементов при отноше­нии L/H< 10 (подкрановых балок, подстропильных балок и т. п.) должен определяться с учетом влияния попереч­ных сил. В этом случае полный прогиб равен сумме про­гибов, обусловленных деформацией изгиба и деформаци­ей сдвига. Прогиб І

Г - 1,5Q<p / = J Q Ух Dx; Ух = —— фсгс,

О

CbhB

Где Q — поперечная сила в сечении х от единичной силы, приложен­ной по направлению искомого перемещения; ф — коэффициент, учи­тывающий длительность действия нагрузки; фсгс—коэффициент, учи­тывающий влияние трещин на деформацию сдвига н принимаемый на участках по длине элементов, где отсутствуют нормальные н наклон­ные трещины, равным 1; на участках, где только наклонные трещи­ны, -- 4,8;

В-

ЗВ ЗВ 1 Фсге = или Ф„с = — Г (х) —

Мх

На участках, где только нормальные нли нормальные н наклонные трещины; Всге — жесткость сечення после образования трещин.

; Полный прогиб элементов определяют с учетом дли­тельности действий нагрузки по формуле

F = h-h+h-fcsc (VII. 132)

Где Fi — прогиб от кратковременного действия всей нагрузки; /г — йрогиб от кратковременного действия постоянной и длительной на­грузок; f3 — прогиб от длительного действия постоянной и длитель­ной нагрузок; /с« — выгиб, вызванный ползучестью бетона от обжа­тии.

Прогибы fi и U вычисляют при значениях if>s и кь, от­вечающих кратковременному действию нагрузки, а про­гиб /з — при значениях i|js и %ь, отвечающих длительному действию нагрузки.

Физический смысл формулы (VII. 132) можно уяснить из рассмотрения диаграммы зависимости F—f, изобра­женной на рис. VII.16.

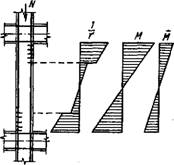
Рис. VII. 17. К определению осред - нениой жесткости Вт внецентрен­но сжатых стоек с учетом пере­менного эксцентриситета продоль­ной силы и трещин на краевых Участках

Полный прогиб предварительно напряженных элемен­тов определяют с учетом длительности действия нагруз­ки по полной кривизне

— I, ум и. IVUf

Т TI ТГ гз Гене 5. Осредненная жесткость железобетонных элементов С учетом трещин в растянутых зонах

При расчёте статически неопределимых железобетон­ных конструкций (например, многоэтажных рамных кар­касов) необходимы значения жесткости элементов или их отношение. Для вне­центренно сжатых элемен­тов с двузначной эпюрой напряжений н с участка­ми по длине без трещин и с трещинами в растянутой зоне необходимо опреде­лять осредненную жест­кость.

Рассмотрим внецен­тренно сжатую стойку ра­мы (без предварительного напряжения) прямоуголь­ного сечения с симметрич­ной арматурой AS=A'S (рис. VII. 17). Продоль­ную сжимающую силу представим как N=M/E0,
А заменяющий момент — как М3=Ме/е0. Тогда из выра­жения кривизны (VII.125) найдем жесткость стойки на участках с трещинами

Й М и /Г (е — Zi) . __Фь_1 ..... В = 17Г = e°h°i[ E, AS (VIM34)

Которая по длине стойки будет переменной в связи с пе­ременным значением эксцентриситетов е0 и других пара­метров. Жесткость стойки на участках без трещин посто­янна и определяется по формуле (VII.112).

. Применение переменной жесткости В для расчета конструкций (например, для расчета статически неопре­делимой рамы) практически неудобно. Поэтому пользу­ются осредненной жесткостью, постоянной по длине эле­мента, которую определяют из условия равенства пере­мещений.

Угол поворота внецентренно сжатой стойки, имеющей по длине различные участки с трещинами и без них, от действия концевых моментов и продольной силы соста­вит

Е = Z JM (1/г) * (Dx).

Этот же угол поворота опорного сечения стойки с ос­редненной по длине жесткостью

Е = Af//6Bm.

Осредненную жесткость внецентренно сжатой стойки определяют из равенства этих двух выражений для угла поворота опорного сечения. Опуская промежуточные вы­кладки, приведем лищь конечный результат, который может применяться для практических расчетов:

Вт = к0Еьіь, (VII. 135)

Где h — момент инерции бетонного сечения стойки; k0 — коэффици­ент, определяемый в зависимости от относительного эксцентриситета E0/H0, коэффициента армирования ц=А,/ЬИо, класса бетона, класса арматуры.