Напряжения в бетоне и арматуре в сечениях с трещиной
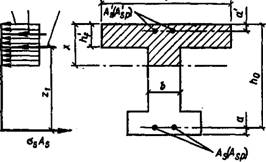
Рассмотрим изгибаемый элемент двутаврового сечения после образования трещин (рис. VII.11). Бетон
6ІСЛ£ *Sc Nb+NsС
Рис. VII.11. К определению напряжений в бетоне и арматуре элемента таврового сечения с полкой в сжатой зоне
Ч
M
*ъАьш
<М
>5 «а
Растянутой полки в сечении с трещиной не работает. Начнем с анализа напряженного состояния при отсутствии предварительного напряжения. Будем исходить из следующих положений:
В зоне чистого изгиба средние сечения, расположенные между трещинами и испытывающие слева и справа симметричные воздействия, после изгиба остаются плоскими;
Зависимость между высотой сжатой зоны в сечении с трещинами х и средней высотой сжатой зоны выражается эмпирической формулой
0,7
ІООц+1 '
(VII. 78)
Ер = =1-
Хе
3) участок бетона растянутой зоны над трещиной в. Расчете не учитывается; влияние этого участка в некоторых случаях существенно, одчако необходимые данные для практического учета этого фактора пока не накоплены.
Исходя из этих положений, выразим напряжения в бетоне и арматуре сжатой зоны сечения с трещиной через напряжения в растянутой арматуре оа и определим высоту сжатой зоны. Деформации бетона сжатой зоны у края сечения
Е _£ьт =—£а__ в Ї—(vn<79)
% H — Xm % (Fh0 — X I|)6 Напряжение в бетоне у края сечения
О = е. = —— —~^ <v, (VII.80)
6 6 фЛ0 — [1] уфь
Напряжение в сжатой арматуре на расстоянии а' от края
А; = Eb eb = JLZ3SL JL 0s. (VII.81)
6 b *m фЛ0 — X
Запишем уравнение равновесия внутренних усилий в сечении с трещиной:
А8л8-аьль(0-а;л;=0, (VII.82)
Где
Аь = Bx + (B'F — B) H'F; (VII.83)
Ю — коэффициент полноты эпюры напряжений бетона сжатой зоны; сведения о вводимой в расчет ширине сжатой полки bf изложены в гл. III.
/
ФH0 — K Vi|>B S 6 Fh0—X І|>ь
Подставим в уравнение (VII. S2) значения аь и As по (VII.80), (VI 1.81):
(VII. 84)
Уравнение (VII.84) после умножения его на (ф/г0— —X)LoABho, подстановки значения Ль и преобразования приводится к квадратному уравнению относительно высоты сжатой зоиы:
Где Р = |т|>ь/(0Хьг|>5; (VII. 86)
Ф, = [(&;- 6) Л) + (vA„) As]/bh0. (VII.87)
Разделив уравнение (VII.85) на Hi и отбросив в свободном члене значение ц'а'/цЛо как малое в сравнении с единицей, получим
S2H-(P + v')i —Рф = 0; (VII.88)
Отсюда относительная высота сжатой зоны в сечении с трещиной
(VII. 89)
Если высота сжатой зоны окажгтся X<Hf, ее следует определить вторично, рассматривая сечение как прямоугольное с шириной сечения Bf.
Обратим внимание, что произведение ыХь в формуле (VII.86) при кратковременном действии нагрузки слабо зависит от формы эпюры нормальных напряжений бетона сжатой зоны. Например, при прямоугольной эпюре напряжений <о=1, и поскольку такая эпюра напряжений вызвана развитием неупругих деформаций, коэффициент А, ь=0,5; следовательно, (oJls=0,5. При треугольной эпюре напряжений в прямоугольном сечении ш = 0,5 и коэффициент Хь = = 1; следовательно, и в этом случае шА, й = 0,5. Поэтому при определении высоты сжатой зоны для удобства расчета принята прямоугольная эпюра напряжений (см. рис. VII.11).
При длительном действии нагрузки под влиянием ползучести бетона сжатой зоны нейтральная ось перемещается и высота сжатой зоны увеличивается (рис. VII.12).
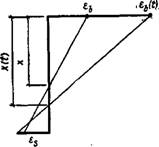
Рис. VII.12. Увеличение высоты сжатой зоны с течением времени
Нормы рекомендуют принимать приближенно высоту
сжатой зоны в сечении с трещиной одинаковую при кратковременном и длительном действии нагрузки и определять ее для изгибаемых и внецентренно загружённых элементов (предварительно напряженных и без предварительного напряжения) по эмпирической формуле
І=іЯі,8+1 + 5(6 + 7Ти h*±3L—t (VII.90)
Но не более 1. Для второго слагаемого правой части формулы (VII.90) верхние знаки принимают при сжимающем усилии Nm, нижние знаки —при растягивающем усилии Ntot.
В формуле (VII.90) фу определяют по формуле (VII.87); для предварительно напряженных элементов вместо A'S принимается A'Sp, значение Хь — отвечающее кратковременному действию нагрузки; согласно нормам, ХЙ==0,45;
T = Y'{-Hf№0) (VII.91)
В формулу (VII.91) для прямоугольных сечений вместо А/ подставляют 2а';
6 = Ma/Bf%RbtSer, (VII.92)
Где Ма — заменяющий момент, т. е. момент относительно оси, проходящей через центр тяжести растянутой арматуры, от внешних сил и усилия предварительного обжатия Р, определяемый по формулам:
Для изгибаемых элементов
Ms = М+Реар (VII. 93)
Для внецентренно сжатых и внецентренно растянутых элементов
Ма = Ne + Pesp-, (VII. 94)
Е3р — расстояние от точки приложения усилия предварительного обжатия Р до оси, проходящей через центр тяжести растянутой арматуры; е — расстояние от точки приложения усилия от действия внешней нагрузки N до оси, проходящей через центр тяжести площади растянутой арматуры.
Высоту сжатой зоны в сечении с трещиной по приведенным формулам определяют приближенно, однако на результаты расчета раскрытия трещин, кривизн, прогибов и т. п. во многих случаях это не оказывает существенного влияния.
Плечо внутренней пары сил для таврового сечения при прямоугольной эпюре напряжений в бетоне сжа
той зоны равно расстоянию между усилием в растянутой арматуре и равнодействующей усилий в бетоне и арма туре сжатой зоны (см. рис. VII.11). Его можно опреде лить из отношения статического момента площади при веденного сечения сжатой ЗОНЫ Sred относительно оси проходящей через центр тяжести растянутой арматуры к площади приведенного сечения
Г_ Sred _Sh+(vAbKK-fl')
Zl Ared (<Pt + І) BK
После преобразований
' Fa/Hp) Ф, + Г 2(Ф/ + 8
Напряжение в бетоне сжатой зоны в сечении с трещиной найдем из равенства моментов внешних сил и усилия предварительного обжатия Р моменту внутренних усилий относительно оси, проходящей через центр тяжести площади растянутой арматуры,
Ms = Ob (Ф/ + І)іА0 Zi, (VII. 96)
Отсюда
<гь = ЛШГ' + 0 4Ао *iJ = MJWC. (VII. 97)
Знаменатель выражения (VII.97) представляет собой упругопластический момент сопротивления после образования трещин по сжатой зоне
Wc — (ф/ +1) Bh0 Zf. (VII. 98)
Приращение напряжения в растянутой арматуре, после того как момент внешних сил превысит момент усилия предварительного обжатия, найдем из уравнения моментов в сечении с трещиной. Момент внешних сил и усилия предварительного обжатия относительно оси, проходящей через точку приложения равнодействующей усилий бетона и арматуры сжатой зоны, равен моменту внутреннего усилия
Ms — Ntot Zi = As Zi і (VII.99)
Отсюда
= (М5 — NM z^/Asp Zi. (VII. 100)
Знаменатель выражения (VII.100) цредставляет собой упругопластический момент сопротивления после образования трещин по растянутой зоне:
(VII. 95)
Zi — Л„
Wa = AaPZi или №8 = л8гх. (VII. 101;
Формула (VII. 100) после подстановки значения Ма по (VII.93), (VII.94) и с учетом значения Nioi по (VII.71) принимает вид:
Для изгибаемых элементов
<xs = [М - Р (zi - Esp)]/Ws-, (VII. 102)
Для внецентренно сжатых элементов
0S = [JV (е— гд -P(Zi- EsP)]/Ws; (VII. 103)
Для внецентренно растянутых элементов
As = [JV(* + 2l)-P(zi-*sp)]/ttV (VII. 104)
Для внецентренно растянутых элементов при EA,Tot< <0,8 h0 значение os определяют по формуле (VII. 104), принимая гх равным Zs — расстоянию между центрами тяжести растянутой и сжатой арматуры.
Для изгибаемых элементов без предварительного напряжения:
<хь = Af/Wc; (VII. 105)
Os = M/Ws. (VII. 106)
Полученные значения as подставляют в расчетные формулы при определении ширины раскрытия трещин.
4. Расстояние между трещинами
Приращение напряжений в растянутой арматуре, после того как момент внешних сил М превысит момент
Усилия предварительного обжатия Мгр в сечении с трещиной as, crc (как только она появилась), найдем из условия, что при переходе сечения из стадии I в стадию II изгибающий момент один и тот же Mere■ Тогда с учетом выражения (VII.29)
Os. crc = (МСГС — Мгр)/Ws = = Rbt,SerWpl/Ws. (VII. 107)
3FVOpO?C
![]()
-Эпюра т.
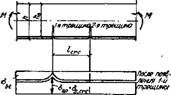
Рис. VI 1.13. Напряженное состояние изгибаемого элемента при образовании трещин
Расстояние между трещинами в зоне чистого изгиба lav, найдем, как и при
центральном растяжении, из условия, что разность усилий в растянутой арматуре в сечениях с трещиной и между трещинами уравновешивается усилием сцепления арматуры с бетоном (рис. VII. 13). Тогда, согласно уравнению (VII.68),
(о8р + аз, сгс) Л3р — (а3р + 2VRbtlser) Аср = тс Alcrc со,
После подстановки значения As,Crc по (VII.107)
(Wpl/W3 - 2v) %,8ЄГ А,Р = тс Alcrc <■>. Отсюда расстояние между трещинами
/сгс = (Wpi/VW, - 2) VuRbt,Ser/°>Тс (VII • 108)
Или
LCTC = K1Vu ті; (VII. 109)
K^WpihW^-li (VII. 110)
Где и, г) имеют такие же значения, как н в (VII.70) при центральном растяжении.
Расстояние между трещинами в элементах без предварительного напряжения также определяют по формуле (VII. 109).
Закрытие трещин, нормальных и наклонных к продольной оси элемента, должно быть обеспечено в предварительно напряженных конструкциях, отвечающих требованиям 2-й категории трещииостойкости. Это обусловлено тем, что для коррозии арматуры наиболее опасно продолжительное раскрытие трещины. Если при полной нагрузке — кратковременной и длительной — образуются трещины, то при снижении нагрузки до длительно действующей они закроются лишь при условии, что арматура работала упруго, необратимые деформации не возникали.
Для надежного закрытия трещин, нормальных к продольной оси элемента, должны соблюдаться требования:
1) ®зР + °s < 0,8RStSer,
Где Стер — предварительное напряжение в арматуре с учетом всех потерь; а, — приращение растягивающего напряжения в арматуре от действия виешинх нагрузок; K — коэффициент, принимаемый: для высокопрочной проволочной арматуры равным 0,65; для стержневой арматуры — 0,8;
2) сечение с трещиной в растянутой зоне при постоянной и длительной нагрузках должно оставаться обжатым с нормальными напряжениями на растягиваемой внешними нагрузками грани: аь^0,5 МПа.
Сжимающие напряжения аь определяют для упругого приведенного сечения от действия внешних нагрузок и усилия предварительного обжатия Р.
Для надежного закрытия трещин, наклонных к продольной оси элемента, оба главных напряжения amt= = Omc на уровне центра тяжести приведенного сечения должны быть сжимающими и по значению аь^0,5 МПа. Чтобы обеспечить это требование, может оказаться необходимым создание двухосного предварительного напряжения (с помощью напрягаемых хомутов или отогнутых стержней).