Железобетон

КОНСТРУКЦИИ МНОГОЭТАЖНЫХ ГРАЖДАНСКИХ ЗДАНИИ

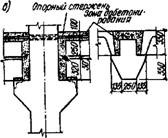
Рис. XV.13. Конструкция узлов сборио-монолитной многоэтаж­ной рамы

А — до замонолнчивання; б — после замонолнчивання

1. Конструктивные схемы зданий

Многоэтажные гражданские каркасные и панельные (бескаркасные) здания проектируют для массового стро­ительства высотой 12—16 этажей, а в ряде случаев — высотой 20 этажей и более. Сетка колони, шаг несущих гстен и высоты этажей выбирают в соответствии с требо­ваниями типизации элементов конструкций и унифика­ции габаритных параметров. Конструктивные " схемы ' зданий, возводимых из сборных элементов, характерны

Ь-
постоянством геометрических размеров по высоте, perys| •лярностыо типовых элементов конструкций, четким реше-1 нием плана. ' '

Каркасные конструкции применяют для различных! административных и общественных зданий с большими1 помещениями, редко расположенными перегородками, а в некоторых случаях и для жилых домов высотой более 25 этажей. Основными несущими конструкциями много­этажного каркасного здания в гражданском строитель­стве являются железобетонные рамы, вертикальные свя - зевые диафрагмы и связывающие их междуэтажные пе­рекрытия.

При действии горизонтальных нагрузок обеспечение совместной работы разнотипных вертикальных конструк­ций в многоэтажном здании достигается благодаря вы­сокой жесткости при изгибе в своей плоскости между­этажных перекрытий, работающих как горизонтальные диафрагмы. Сборные перекрытия благодаря сварке за­кладных деталей и замоноличиванию швов между от­дельными плитами также обладают высокой жесткостью при изгибе в своей плоскости.

Важнейшим условием достижения высоких эксплуа­тационных качеств многоэтажного здания является обес­печение его надежного сопротивления горизонтальным нагрузкам и воздействиям. Необходимая пространствен­ная жесткость такого здания достигается различными вариантами компоновки конструктивной схемы, в основ­ном отличающимися способами восприятия горизонталь­ных нагрузок.

Например, при поперечных многоэтажных рамах и по­перечных вертикальных связевых диафрагмах горизон­тальные нагрузки воспринимаются вертикальными конст­рукциями совместно и каркасное здание в поперечном направлении работает по рамно-связевой системе, при этом в продольном направлении при наличии только вер­тикальных связевых диафрагм здание работает по свя­зевой системе (рис. XV.14, а).

При поперечном расположении вертикальных связе­вых диафрагм и продольном расположении многоэтаж­ных рам здание в поперечном направлении работает по связевой системе, а в продольном направлении — по рамной системе (рис. XV.14,б). Конструктивная схема каркаса при шарнирном соединении ригелей с колонна­ми будет связевой в обоих направлениях.

Рис. XV. 15. Конструктивный план панельного здания

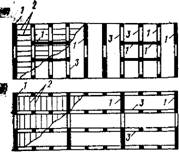
1 — поперечные несущие пане­ли стен; 2 — продольные несу­щие панели стен; 3 — плнты перекрытия; 4 — навесные па­нели ограждающих стен

Рис, XV. 14. Конструктивные 'Планы каркасных многоэтаж­ных гражданских зданий в — с поперечными рамами; й — с продольными рамами; 1 — связевые диафрагмы; 2 — Ланели перекрытий; 3 — рнге - " ли рам

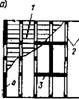
Рис. XV.16. Конструктивный план многоэтажного каркасно­го здания с центральным яд - — ром жесткости

1 — ригели рам; 2 — плиты пе­рекрытия; 3 — ядро жесткости

О.) 1

■ • ■ ■ Q •

■ ■ » » ■ UmJ •

Рис. XV. 17. Конструктивные планы многоэтажных каркас­ных зданий а — с двумя ядрами жестко­сти; б — с двумя ядрами жест­кости, сложной конфигурации, возводимые методом подъема перекрытий; 1 — плнты пере­крытия; 2 — ригели рам; 3 — ядро жесткости двутаврового профиля; 4 — связевые диа­фрагмы; 5 — замкнутое ядро жесткости; 6 — монолитное безбалочное перекрытие

Конструктивные схемы многоэтажных каркасных зда­ний, воспринимающих горизонтальные нагрузки по рам - но-связевой системе, как имеющие лучшие технико-эконо­мические показатели, нашли широкое применение в ^строительстве, особенно в сейсмических районах страны.

Панельные конструкции применяют для жилых до­мов, гостиниц, пансионатов и других аналогичных зда­ний с часто расположенными перегородками и стенами. В панельных зданиях основными несущими конструк­циями служат вертикальные диафрагмы, образованные панелями внутренних несущих стен, расположенными в поперечном, иногда в продольном направлении, и связы­вающие их междуэтажные перекрытия. Панели наруж­ных стен навешивают на торцы панелей несущих попе­речных стен. Многоэтажное панельное здание как в поперечном, так и в продольном направлении восприни­мает горизонтальную нагрузку по связевой системе (рис. XV. 15). Возможны другие конструктивные схемы много­этажных зданий. К ним относятся, например, каркасное здание с центральным ядром жесткости, в котором в ка­честве вертикальных связевых диафрагм используются внутренние стены сблокированных лифтовых и вентиля­ционных шахт, лестничных клеток (рис. XV.16); здание с двумя ядрами жесткости открытого профиля — в виде двутавров (рис. XV. 17,а); здание с двумя ядрами жест­кости и сложной конфигурацией в плане, позволяющей индивидуализировать архитектурное решение (рис. XV. 17, б). В описанных конструктивных схемах зданий горизонтальные воздействия воспринимаются по рамно - связевой или связевой системе.

В зданиях с центральным ядром жесткости в целях обеспечения удобной свободной планировки сетку колонн укрупняют, в ряде решений внутренние колонны исклю­чают и элементы перекрытий опирают на наружные ко­лонны и внутреннее ядро жесткости. Ригели перекрытий пролетом 12—15 м проектируют предварительно напря­женными, шарнирно связанными с колоннами, панели перекрытий — пустотными или коробчатыми. Горизон­тальное воздействие на здание воспринимается вв* свя­зевой системе.

В зданиях с двумя ядрами жесткости и сложной кон­фигурацией в плане перекрытия выполняются монолит­ными в виде безбалочной бескапительной плиты. Возво­дят такие здания методом подъема перекрытий (или подъема этажей). Конструктивно-технологическая сущ­ность этого метода состоит в том, что полигоном для изготовления перекрытий служит перекрытие над под­валом. Перекрытия бетонируют одно над другим в виде пакета с разделяющими прослойками. В местах, где цроходят колонны, в перекрытии оставляют отверстия, окаймленные стальными воротниками, заделанными в бетоне. В проектное положение перекрытие поднимают с ромощью стальных тяжей и гидравлических домкратов, Остановленных на колоннах верхнего яруса. После подъ­ема перекрытия в проектное положение стальные ворот - йики крепят к стальным деталям колонн на сварке. При ртой конструктивной схеме восприятие горизонтального воздействия на здание осуществляется по связевой сис­теме, а при обеспечении конструктивной связи плит пере­крытий с колоннами — по рамно-связевой системе, в ко­торой ригелями служат безбалочные плиты.

2. Основные вертикальные конструкции

Многоэтажные рамы высотой до 16 этажей имеют ко­лонны постоянного сечения по всей высоте здания (рис. XV.18, а). Увеличение несущей способности колонн ниж­них этажей достигается повышением класса бетона, про­цента армирования, применением жесткой арматуры. Элементы сборных колонн в целях снижения трудоемко­сти на монтаже выполняют размером на 2—4 этажа.

Комбинированные вертикальные связевые диафрагмы, состоящие из сплошной и рамной частей, сохраняют ре­гулярную структуру — размеры элементов и пролетов ригелей —по всей высоте здания (рис. XV.18, б). Верти­кальные связевые диафрагмы с проемами и ядра жест - кости имеют железобетонные перемычки, жестко свя­занные на опорах с простенками, и также сохраняют регулярную структуру по всей высоте здания (рис. XV. 18, в).

' Стыки ригелей с колоннами выполняют жесткими на консолях, бесконсольными и шарнирными (см. гл. XI)! При жестком соединении ригелей с колоннами сущест­венно повышается общая жесткость многоэтажного зда­ния"'и достигается экономия металла на армирований рйгелей (по условиям прочности, трещиностойкости и йредельных прогибов).

'Элементами сборных вертикальных связевых диаф - |)йгм являются колонны каркаса и панели с полками для опирання плит перекрытий (рис. XV.19). Элементы сое­диняют сваркой закладных деталей и замоноличиванием. Применяют также монолитные панели, бетонируемые на

Рис. XV. 18. Основные верти­кальные конструкции много­этажных зданий а — многоэтажные регулярные рамы; б — связевые комбини­рованные диафрагмы; в — свя­зевые диафрагмы с проемами

Рис. XV.19. Соединение эле­ментов вертикальной связевой диафрагмы

— колонны каркаса здания;

— панели диафрагмы; 3 —> полки для опирання панелей перекрытий; 4—монтажная сварка; 5 — закладные детали колонн; 6 — стыковые стержни; 7 — закладные детали панелей

Диафрагмы

В)

6)

To

В-в

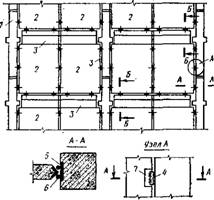
Месте возведения после приварки к закладным деталям колонн арматурных сеток.

Вертикальные связевые диафрагмы в виде ядер жесткости чаще выполняют монолитными в скользящей опалубке. В сборных ядрах жесткости элементы стенок малоповторяемы; кроме того, из-за значительных сдвига­ющих усилий, возникающих в углах стенок, на монтаже увеличивается объем сварочных работ.

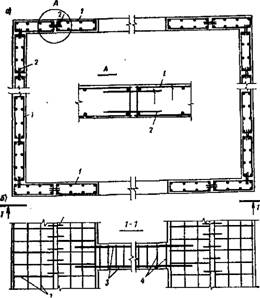
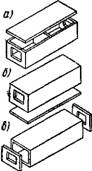
Рис. XV.20. Схема конструирования арматуры монолитного ядра

Жесткости

А — сечение в плане; б— вид сбоку; 1 — арматурный пространствен" ный каркас; 2 — соединительные стержни; 3 — продольная арматура перемычки; 4 — поперечная арматура перемычки

Монолитные ядра жесткости армируют вертикальны - ми пространственными каркасами, которые на монтаже стыкуются соединительными стержнями (рис. XV.20). Перемычки над проемами армируют горизонтальными Каркасами. Продольная и поперечная арматура ядер жесткости и перемычек назначается по расчету. Толщина стенок ядер жесткости устанавливается по расчету, обыч­но 200—400 мм. По условиям технологии возведения в скользящей опалубке наименьшая толщина стенок 200 мм. Стены и перемычки ядер жесткости могут быть предварительо напряженными. Для монолитных ядер жесткости применяют бетон классов В15, В25.

Панели внутренних несущих стен в панельных здани­ях по условиям требуемой звукоизоляции выполняют из тяжелого бетона толщиной 14—16 см. При такой толщи - *не обеспечивается несущая способность этих панелей в

Объемный злемент

Рис. XV.21. Конструкции многоэтажного жилого дома из объемных блоков

А — блок-стакан; б — блок-колпак; в —• блок-трубы; г — многоэтажный дом

Зданиях высотой до 16 этажей. Увеличение несущей спо­собности панелей стен зданий большей высоты достига­ется применением в нижних этажах бетона более высо­кого класса, увеличением толщины железобетонных панелей.

Бетонные панели несущих стен армируют конструк­тивной вертикальной арматурой у каждой поверхности панели в количестве 0,3 см2 на 1 м длины горизонталь­ного сечения панели. Площадь сечения горизонтальной распределительной арматуры у каждой грани должна составлять не менее 0,3 см2 на 1 м вертикального сече­ния. Железобетонные панели несущих стен армируют двойной вертикальной арматурой так, чтобы у каждой поверхности минимальный процент армирования гори­зонтальных сечений при бетоне класса В15 составлял 0,1, а при бетоне класса В25 или ВЗО —0,15. Чтобы по­высить сопротивление опорных сечений железобетонных панелей (с целью компенсации обрываемой продольной арматуры), применяют косвенное армирование приопор - ных участков сетками.

Дальнейшим усовершенствованием конструкции па­нельного здания может считаться конструкция из желе­зобетонных объемных блоков на комнату или на квар­тиру, изготовленных на заводе с полной внутренней от­делкой. Такая конструкция имеет самую высокую завод­скую законченность и требует минимальных трудовых затрат на монтаже. В зависимости от технологии изго­товления различают объемные блоки трех типов: блок - стакан с отдельной панелью потолка, блок-колпак с от­дельной панелью пола и блок-труба (рис, XV.21). Объ-
:емные блоки перечисленных типов изготовляют на заво« дах монолитными или сборными из отдельных панелей. Способ опирання блоков один на другой предопределя­ет характер работы конструкции здания под нагрузкой. При полосовом опирании блоков на растворный шов создаётся конструктивная схема панельного здания с не­сущими стенами, работающими на сжатие, при точечном опирании на углы или внутренние пилястры — конструк­тивная схема здания с несущими стенами, работающи­ми в своей плоскости на изгиб.

§ XV.3. СВЕДЕНИЯ О РАСЧЕТЕ МНОГОЭТАЖНЫХ РАМ

1. Предварительный подбор сечений

" Плоские рамы, расположенные с определенным ша­гом и Связанные перекрытиями, образуют пространст­венный блок рам с размерами в плане, равными расстоя - , нию между температурными швами или наружными сте­нами. Вертикальные постоянные и временные нагрузки, а также горизонтальные ветровые нагрузки приложены одновременно ко всем рамам блока, поэтому пространст­венный характер работы в этих условиях не проявляется и каждую плоскую раму можно рассчитывать в отдель­ности на свою нагрузку.

Многоэтажная железобетонная рама статически не­определима, и для ее расчета необходимо предвари­тельно подобрать сечения ригелей и стоек, определить их жесткости или установить отношение жесткостей. С этой целью пользуются примерами ранее запроектированных аналогичных конструкций или предварительно прибли­женно подбирают сечения. Высоту сечения ригеля опре­деляют по формуле

Где Лї=0,6...0,7 Мъ здесь М0 — изгибающий момент ригеля, вычис­ленный как для однопролетиой свободно лежащей балки.

Площадь сечений колонн находят по приближенной, формуле

А= (1,2 ... 1-,5)N/Rb.

"По результатам предварительного подбора сечений производят взаимную увязку сечений ригелей и стоек и округляют их размеры до унифицированных. Момент - инерции сечений ригелей и стоек определяют, как для

W? /Я7 777f ffff ОТ

R~m

■H-

Г7Л

Ш

Rm

Ші Ш

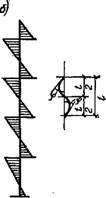
Рис. XV.22. Расчетные схемы многоэтажных рам (а) и эпюра мо­ментов многоэтажной колонны (б)

Сплошного бетонного сечения. При монолитных перекры­тиях момент инерции ригелей определяют, как для тав­ровых сечений с шириной полки, равной шагу рам.

2. Усилия от нагрузок

Многоэтажные многопролетные рамы каркасных зданий имеют преимущественно однообразную (регуляр­ную) расчетную схему с равными пролетами или со сред­ним укороченным пролетом на оси симметрии, а также с одинаковой нагрузкой по ярусам (рис. XV.22,а). Узлы стоек таких рам, расположенные на одной вертикали, имеют примерно равные углы поворота и, следовательно, равные узловые моменты с нулевой точкой моментов в середине высота этажа (рис. XV.22, б). Это дает осно­вание расчленить многоэтажную раму на ряд одноэтаж­ных рам с высотой стоек (колонн), равной половине вы­соты этажа, с шарнирами по концам стоек, кроме пер­вого этажа.

На вертикальную нагрузку необходимо рассчитывать три такие одноэтажные рамы: верхнего, среднего и пер­вого этажа. Если число пролетов рамы больше трех, ра­му практически заменяют трехпролетной рамой и пола-

Р

Т изгибающие моменты в средних пролетах много­летной рамы такими же, как и в среднем пролете хпролетной рамы, р При расчете по методу перемещений число неизвест­ных углов поворота равно числу узлов в одном ярусе вамы. Горизонтальным смещением при вертикальных Іагрузках обычно пренебрегают. При расчете по методу сил в качестве неизвестных принимают опорные момен - |ы ригелей одного яруса рамы и сводят задачу к реше­нию трехчленных уравнений балки на упруговращаю - Щихся опорах. Расчет также можно выполнять по таб­лицам прил. XI. Если ригель рамы на крайних опорах Цюрнирно опирается на несущие наружные стены, рас­чет также предусмотрен табл. 1 прил. XI. В таблицах опорные моменты ригелей рамы, имеющей колонны с одинаковыми сечениями:

M = (*g + £*)<!,

|уде a, j3 — табличные коэффициенты, зависящие от схемы загруже - 1 {имя постоянной и временной нагрузками и от отношения суммы по- Йгонных жесткостей стоек, примыкающих к узлу, к погонной жестко - JfeTH ригеля; g, v — постоянная и временная нагрузки на 1 м ригеля; / — пролет ригеля между осями колонн.

Изгибающие моменты в стойках для каждой схемы загружения рамы определяют по разности опорных мо­ментов ригелей в узле, распределяя ее пропорциональ­но погонным жесткостям стоек.

Изгибающие моменты в пролетных сечениях ригелей, а также поперечные силы определяют обычными спосо­бами как в однопролетной балке, загруженной внешней нагрузкой и опорными моментами по концам.

513

При расчете рам целесообразно учитывать образова­ние пластических шарниров и выравнивать изгибающие Моменты для достижения экономического и производст­венного эффекта: облегчения сборных стыков, увеличе­ния повторяемости элементов опалубки и арматуры, упрощения армирования монтажных узлов, облегчения условий бетонирования их и т. п. Для этого раму (как и ригель балочного перекрытия) рассчитывают на дей­ствие постоянной нагрузки и различных загружений временной нагрузкой как упругую систему. Затем для каждого из перечисленных загружений строят свою до­бавочную эпюру моментов, которую суммируют с эпю­рой упругой системы.

«3—943

Величина выравненного момента не оговаривается, но для его определения следует выполнить. расчеты по предельным состояниям второй группы! 'Йрактичёскй'не­обходимо, чтобы выравненный момент в расчетном сече - ни составлял не менее 70 % момента в упругой схеме. •

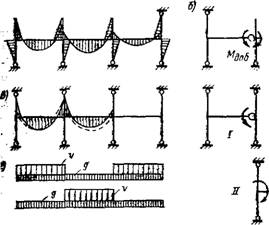
В рамных конструкциях целесообразно намечать ста образования пластических щарнирйв на опорах ри­гелей и уменьшать опорные моменты. Допустим, что ра­ма рассчитана как упругая система и для определенного загружения получена эпюра моментов (рис. XV.23, а) . Если теперь для Этого же загружения строить добавоч­ную эпюру моментов, то добавочный опорный момент ДМ будет заданной величиной, и вследствие этого рассмат­риваемую раму и систему канонических уравнений рас­членяют на две более простые системы с меньшим чис­лом неизвестных (рис. XV.23, б) .' Выравненная эпюра М ригелей рамы изображена на рис. XV.23, е.

При упрощенном способе выравнивания моментов ри­гели многоэтажных и многопролетных рам загружают временной нагрузкой через пролет и постоянной нагруз­кой во всех пролетах, при этом получают эпюру момен­тов с максимальными моментами в пролетах и на стой­ках, которую принимают в качестве выравненной эпюры моментов (рис. XV.23,г). Опорные моменты ригелей в такой выравненной эпюре моментов При отношениях ин­тенсивности временной и постоянной нагрузок vjg^. 5 обычно составляют не менее 70 % максимального мо­мента в упругой схеме, В расчете по выравненным мо­ментам необходимо, чтобы в сечениях стоек рам момент продольной силы относительно центра тяжести сжатой зоны составлял не менее 70соответствующего момен­та в упругой схеме, а в сечениях стоек рам, работающих по случаю 2, кроме того, воспринималась полная про­дольная сила и, по крайней мере, половина изгибающего момента в упругой схеме.

Расчет на горизонтальные (ветровые) нагрузки вы­полняют приближенным методом. Распределенную гори­зонтальную нагрузку заменяют сосредоточенными сила­ми, приложенными к узлам рамы (рис. XV.24). Нулевую точку эпюры моментов стоек всех этажей рамы, кроме первого, считают расположенной в середине высоты эта' жа, а в первом этаже при защемлении стоек в фунда* менте — иа расстоянии 2/3 высоты от места защемленияі

Ярусные поперечные силы рамы

Щштіііш <L

1Ґ f

Пластический шарнир ;

-г

Т

Ib

А

Л

Fie if if

Рис. XV.23. К расчету многоэтажных рам на вертикальные нагрузки по вы - равненнкм моментам

Рнс. XV.24. К расчету многоэтажных рам на горизонтальные нагрузки

І Qi = Fi + Pfb... Q2 = F2 4- F3 + ... +F» ИТ. д.;

Q=Qk

(XV. 1)

(s/f4

Вдесь В -=■ жесткость сечения стойки; т — число стоек в ярусе.

Крайние стойки рамы, имеющие степень защемления в узле меньшую, чем средние стойки (поскольку к край­нему узлу примыкает ригель только с одной сторны), ^воспринимают относительно меньшую долю ярусной по­перечной силы, что учитывается в расчете условным

Они распределяются между отдельными стойками про­порционально жесткостям:

Таблица XV. I. Значения коэффициента Р для уменьшения жесткости крайних стоек многоэтажных рам прн расчете на горизонтальные нагрузки

Обозначения: і=В/1 — погонная жесткость ригеля крайнего пролета; і погонная жесткость крайней стойки, примыкающей к узлу снизу.

Уменьшением жесткости крайних стоек путем умноже­ния на коэффициент р<1, определяемый по табл. XV.1.

По найденным поперечным силам определяют изгиба­ющие моменты на стойках всех этажей, кроме первого:

M = Ql/2. (XV. 2)

Для первого этажа изгибающий момент стойки в верхнем и нижнем сечениях

М = Q//3; М = Q2//3. (XV.3)

При определении опорных моментов ригелей суммар­ный момент в узле рамы от выше и ниже расположен­ных стоек распределяется между ригелями пропорцио­нально их погонным жесткостям. В крайнем узле момент ригеля равен сумме моментов стоек.

3. Расчетные усилия и подбор сечений

На основании эпюр моментов и поперечных сил рамы от различных загружений строят огибающие эпюры М и вычисляют соответствующие им продольные силы N для основных и дополнительных сочетаний нагрузок.

Для расчетных сечений по огибающим эпюрам долж­ны быть найдены значения Мтах и Літг„ и соответствую-, щие им значения N, а также Nmax и соответствующие им М. Расчетные усилия могут быть найдены также состав­лением таблицы, куда вписывают значения усилий, соот­ветствующие отдельным загружениям. Расчетными сече­ниями для ригелей являются сечения на обеих опорах и в пролете, для колонн — сечения вверху, внизу и, кроме; того, для высоких колонн — в одном-двух промежуточ-. ных сечениях по высоте. :

Сечения ригелей и стоек подбирают как для изгибае­мых и сжатых элементов. Если моменты имеют разные; знаки, но близки по величине, сечения армируют с сим-

Ош

І w%

>KK

A

77Г

777

-ъ-L

В)

Б) Гп

1 rf

ІРнс. XV.25. Расчетные схемы (а, б) и перемещения многоэтажной

Рамы (в)

Метричной арматурой. Расчетную длину стоек принима­ют в зависимости от условий закрепления в узлах.

Для расчета усилий многоэтажных рам с применени­ем ЭВМ имеются разработанные программы.

Горизонтальные перемещения

Г Расчетной схемой многоэтажного многопролетного каркасного здания, работающего по рамной системе, яв­ляется многоэтажная рама, жесткости ригелей и стоек которой равны соответствующим суммарным жесткостям всех рам здания (рис. XV.25, а). При расчете горизон­тальных перемещений, как показали исследования, мож­но допустить равенство углов поворота узлов яруса мно­гоэтажной рамы и принять соответствующую расчетную Схему, изображенную на рис. XV.25, б, в которой Si — сумма погонных жесткостей стоек этажа; гг—сумма Жесткостей ригелей этажа, деленная на осредненный яролет ригелей I (возможна сумма погонных жесткостей ригелей этажа); U — высота этажей; п — число этажей. ' Горизонтальные перемещения от действия силы F =1 Ъ принятой расчетной схеме равны:

Ви= (1/12) (Si + (XV.4|

Bkk = (m){Sk + Rk + lllArh)-, £=2,3 (XV. s|

Shi = 8{fc = «м+і = ••• =6ft7v = 6ftft + 'fe/ftW48rfti (XV. б):

Где

= +0.335^; (XV. 8)

Я2 = (k + /2)-2/(4гі + 0,33^); (XV. 9)

Rb=Rh-i+(h-i + kYI4rh-l-> *=3, 4,..., п. (XV. 10^

В формулах (XV.4) и (XV.5) первое слагаемое Su от­ражает влияние жесткости стоек на перемещения много-, этажной рамы, второе слагаемое Rh — влияние жестко - сти ригелей. При определении перемещений в предполо­жении полного защемления стоек рамы в узлах необхо­димо принять Rk=0. Однако неучет жесткости ригелей многоэтажной рамы может приводить к существенной погрешности при определении перемещений (в 2—3 раза и даже больше).

Перемещения многоэтажных рам от горизонтальных нагрузок, приложенных одновременно по всем этажам:

У = ЄЙІ Ft + 6ft2 F2 + ... + dhn Fn. (XV. 11)

Перемещения рамы при числе этажей п^6, если принять во внимание, что ярусные поперечные силы

П

Qk = 2 Ft i і > k, і=к

Можно определять как сумму поэтажных линейных пере­косов (взаимных смещений концов стоек) :

Y^j^Qtcr, i<k, (XV. 12)

Где Сі — линейный перекос от единичной силы, приложенной в одном, из верхних этажей.

Для многоэтажной рамы регулярной структуры с по­стоянными по высоте погонными жесткостяМй S, г и оди­наковой высотой этажей I линейный перекос от F=1 можно найти умножением самой на себя эпюры момен­тов на заштрихованных участках (рис. XV.25,6). Тогда

Сдвиговая жесткость многоэтажной рамы К — сила, вызывающая единичный угол перекоса ty = Kc/l=l, от-

К = 1/с, или К= 12/[/(s-i+ /•-!)]. (XV. 14)

|їри числе этажей п^6 дискретное расположение риге­лей можно заменить непрерывным, сосредоточенную на­грузку Pi — распределенной р{х), а суммирование в |XV.12)—интегрированием. Тогда перемещение

* X

У = J Qo (сII) dx = j (Qo/K) dx, (XV. 12a)

О 0

We Qj — поперечная сила от распределенной нагрузки; х—■ коорди­ната горизонтального сечения рамы.

Последовательным дифференцированием выражения (XV.12a) найдем:

КУ' = Q0; (XV. 15)

Ky" =—р(х). (XV. 15а)

Следовательно, при изгибе многоэтажной рамы за­висимость между горизонтальным перемещением и по­перечной силой выражается первой производной, а кри - Твизна у" с точностью до постоянного множителя А рав- ; на внешней нагрузке со знаком минус.

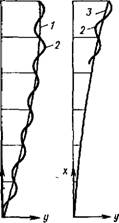
Линия 1 общего изгиба стоек (эпюра смещений яру­сов рамы) обращена вогнутостью в сторону начального положения как у системы, работающей на сдвиг, а ли­ния 2 местного изгиба стоек располагается вокруг ли­нии 1, отклоняясь в пределах каждого этажа в ту и дру­гую сторону (рис. XV.26). В случаях когда стойки ^обладают жесткостью, значительно превышающей же­сткость ригелей, характер общего изгиба стоек меняет­ся— линия 3, при этом поперечная сила By"', зависящая от суммарной изгибной жесткости стоек B—'ZBj, стано­вится весьма существенной. Кроме того, под влиянием деформаций удлинения и укорочения крайних стоек от действия продольных сил N происходит изгиб рамы как вертикальной консольной конструкции, у которой рас­стояние между крайними стойками-поясами равно b, а изгибная жесткость равна В0. В средних стойках много­пролетной рамы с малоотличающимися пролетами про­дольные силы незначительны, так как они равны разно - 'Стн поперечных сил ригелей. Дополнительный угол

Цт. 4—

— Л'

Я

Zo

І

Ft л,

Ріц. XV.26. Перемещения многоэтажной рамы

1 — лииия общего изгиба стоек многоэтажной рамы, деформирую­щейся как сдвиговая система; 2 — линия местного изгиба стоек; 3 — лииия общего изгиба стоек, когда их жесткость значительно пре« вышает жесткость ригелей

Поворота стоек от момента продольной силы в верти­кальной конструкции M=Nb в предположении плоского поворота рамы

С мм ь с

Тогда выражение поперечной силы при учете дефор­маций от продольных сил, согласно (XV. 15):

(XV. 16)

= Qo-

К

(у' + (b/BQ) Г Ndx

5. Общее уравнение многоэтажной системы

Уравнение равновесия поперечных сил в горизон­тальном сечении системы

- By"' + Ку' + (КЫВо) J Ndx = Q0.

(XV. 17)

О

Значение N найдем из уравнения равновесия момен­тов в том же горизонтальном сечении

N = (M0-M)/b=(M0 + By")tb, ' (XV. 18)

•де Mo—момент внешней нагрузки в уровне х М=—By" — суммар­ный изгибающий момент стоек рамы.

После подстановки в (XV. 17) значения N найдем

X

By"' - /Cv? у' - (/С/Во) $ M9dx + Q0 = О, (XV. 17а)

О

Уа после дифференцирования по х получим

By™ - /Cv2 у" - КМаІВ0 - Р(х)= 0. (XV. 19)

Введем для увеличенного в В раз перемещения у обозначение w=By, тогда

4wlv-w"М0-^р(х) = 0, (XV.20)

Где s2 = Yb/KvZ — линейная характеристика; (XV. 21)

V2 = 1 + В/В0. (XV. 22)

Уравнение многоэтажной системы в перемещениях (XV.20) —общее, на его основе решаются системы рам­ные, рамно-связевые, связевые. Если учесть, что М = =—w", его можно свести к дифференциальному урав­нению второго порядка.

Решение уравнения (XV.20) имеет вид

Tci = C1 + C2S2<P + C3sh<p+C4sh<p + C0; (XV.23)

Эдесь Сі — постоянные интегрирования, зависящие от краевых усло­вий; Со — частное решение, зависящее от вида нагрузки;. <$=x/S2 — безразмерная координата.

К — H/s2 — характеристика жесткости при х = Я; (XV.24)

Н = Н0 п/(п — 0,5) — расчетная высота здания; (XV.25)

Но — расстояние от заделки до оси ригеля верхнего яруса.

Для обычных рамных конструкций влиянием перво­го члена уравнения (XV.18) можно пренебречь, и тогда

Ку" + КМ01Ва + р (х) = 0. (XV.26)

Здесь v2 = l, поскольку В—0.

После двукратного интегрирования уравнения (XV.26), определения постоянных интегрирования с уче­том краевых условий г/(0)=0 и Ку'{0) =Qo(0) при рав­номерно распределенной нагрузке р=р[х) и значении

Момента внешней нагрузки Мо=—0,5р(Н — х)2 полу­чим уравнение перемещений многоэтажной рамы: р№ Л рЯ1 / 4 £1 v

Мг(2р"Тр+ 3 )' (xv-27)

Где £=д:JH— безразмерная координата.

При | = 1 прогиб верхнего яруса рамы

Р№ pW pHl (

Где Ki — характеристика жесткости рамы при учете влияния про­дольных сил стоек;

%fr = H К/В0. (XV.29)

Как показали исследования, если Kfr<0,7, влиянием продольных сил стоек многоэтажной рамы можно пре­небречь и принимать в расчетах v2 = l.

Для определения изгибной жесткости Во обозначим; Ли Л2 — суммарные площади сечений левых и правых крайних стоек этажа; Zo— расстояние от оси левых сто­ек до центра тяжести горизонтального сечения (см. рис. XV.26).

Тогда

Г0 = Аг ЬІ(Аі + А2) = Ы( 1 + ЛцМг); (XV.30)

Момент инерции горизонтального сечения

/0 = Аі гі + А2 (6 - Zaf = At bll( + AJAtf, (XV.31) изгибная жесткость рамы

В0 = Еь At &2/( 1 + AilA2y, (XV.32)

Изгибная жесткость при А{=А2=А симметричной рамы

Вй = ЕъАьт. (XV.33)

•Следовательно, жесткость В0 зависит от осевой же­сткости стоек ЕьА.

6. Податливость стыков

Податливость или деформативность стыков сборных железобетонных элементов приводит к некоторому сни­жению жесткости и увеличению горизонтальных проги­бов многоэтажного каркасного здания. Стыки ригелей и стоек вследствие неупругих деформаций закладных де­талей, соединительных стержней и анкеров в бетоне де-

Й) S)

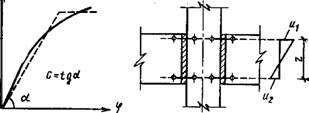
Рис. XV.27. К учету податливости стыков ригелей с колоннами

Формируются. При этом первоначальный угол между гранями стыкуемых элементов под действием изгибаю­щего момента М изменяется на величину угла податли - ївости, равную ф. Средний модуль деформативности сты­ка, или коэффициент жесткости стыка, определяют по ре­зультатам испытаний как тангенс угла наклона секущей на диаграмме М—ц> (рис. XV.27) : С—М/ф.

Угол податливости стыка

<р = (ні + и2)/г, (xv.34)

Где «і, its — измеренные перемещения растянутой и сжатой зон сты­ка за вычетом перемещений, возникающих иа этой же базе измере­ний в монолитных аналогичных стыках; г — расстояние между ося­ми измерительных приборов.

Коэффициент жесткости стыка, кН-м, можно пред­варительно определить в зависимости от высоты сечения стыкуемого элемента по эмпирической формуле

C — 4-Qbh?, где Т] я* 7. (XV.35)

Податливость стыков при определении сдвиговой жесткости рамы А учитывают соответствующим умень­шением погонной жесткости элементов. Если стыки ко­лонн в каждом этаже и стыки ригелей на каждой опо­ре, то:

<'i (1 + Иг) h_

2 2

(XV. 36)

1+4Ц2 ; С2

Где Си Сі — коэффициенты жесткости стыка ригелей и стоек; іи — погонная жесткость ригелей и стоек.

Осевой податливостью обладают стыки колонн так­же под действием продольной силы N. В зоне стыка ко-

—rv

Й)

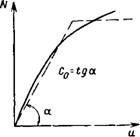
U = ljn

Рис. XV.28. К учету податливости стыков колонн

Лонн развивается дополнительное продольное перемеще­ние и. Коэффициент жесткости стыка Ci—N/u [где и— =ljn{ejn—еь] определяют испытаниями (рис. XV.28). Ко­эффициент жесткости стыков типовых колонн сечением 40X40 см по данным испытаний С/=7-106 кН/м.

Продольные деформации стоек с учетом податливо­сти стыков (при стыках в каждом-этаже)

N

N

N( 1 + И.)

Еь Л ICi Eb А

Где н,„ = Еъ АЦСи (XV.38)

Можно считать, что модуль упругости Еь под влия­нием податливости стыков стоек уменьшается в (І+Цо) раз.

Изгибная жесткость симметричной рамы с учетом податливости стыков стоек, согласно выражению (XV.33),

Ва = Еь АЬЧІ2 (1 + щ)]. (XV.33а)

Аналогично определяют значение В0 для несимметрич­ной рамы.

Как показали исследования, податливость стыков элементов может привести к увеличению горизонтальных перемещений многоэтажного каркасного здания на 20— 40%.

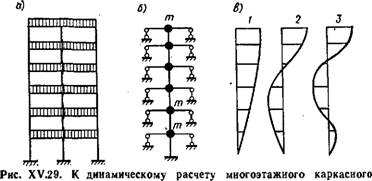
Здания

А — поперечная рама; б — расчетная схема при определении частот и форм свободных горизонтальных колебаний; в — первые три фор­мы свободных колебаний

7. Динамические характеристики

Для многоэтажного каркасного здания (рис. XV.29, а) число частот и соответствующих им форм свободных го­ризонтальных колебаний равно числу этажей (числу степеней свободы). При этом массы перекрытий и ко­лонн считаются сосредоточенными в узлах (рис. XV.29,б). Ярусная масса многоэтажного здания

M=Q/g, (XV. 39)

Где Q — ярусная нагрузка от массы перекрытия, колонн, стен и вре­менной нагрузки; g — ускорение силы тяжести.

Частоты и формы свободных колебаний определяют из уравнений частот, при этом единичные перемещения бік определяют по формулам (XV.4) и (XV.5).

Частоту колебаний первого тона многоэтажной рамы можно определять по формуле

(D^ajVT. (XV. 40)

Где а — коэффициент, зависящий от числа этажей и равный: 1,08— прн ге=3; 1,1—при п—4; 1,12 — при ге=5; /—прогиб верхнего яру­са рамы, определяемый по формуле (XV.11), от горизонтальных сил, равных ярусным маслам, Fh=mk.

При свободных горизонтальных колебаниях много­этажной рамы внешней нагр/узкой будут силы инерции д2 и

Массы, равные — т. При 6 их можно предста­вить в виде распределенной нагрузки

С учетом Ку"=—р(х) получим однородное дифферен­циальное уравнение свободных колебаний

Из решения уравнения с подстановкой у=ХТ найдем

X = Ci sin ах + cos аде, (XV.43)

«- — -^V — . (XV. 45)

Где X — ордината формы свободных колебаний; Т — функция вре­мени;

А = ш ymJKl; (XV.44)

Со — частота свободных горизонтальных колебаний.

Краевые условия: 1) Х(0)=0; 2) АХ'(Н)= 0. При этом получим два однородных уравнения: 1) С2=0; 2) С cos а#=0, из решения которых следует, что cos аН=0; аН= (2i—1) (я/2), где t'= 1, 2, 3,... номер тона свободных колебаний.

Период свободных колебаний, согласно (XV.44),

=—V

О) 2( — 1 V К1

Здесь Я — по формуле (XV.25). Форма свободных коле­баний, согласно (XV.43),

X = Ci sin ах = Сі sin (2і — 1) я|/2. (XV.46)

При определении форм свободных колебаний необ-

ХОДИМЫ лишь отношения перемещений, поэтому в (XV.44) принимают Q — Первые три формы свобод­ных колебаний изображены на рис. XV.29, в.

Если характеристика жесткости рамы^ согласно (XV.29), %fr%0,7, период свободных колебаний опреде­ляют с учетом продольных сил стоек

Ті = а, нУт/кї, (XV. 47)

Где 0( — коэффициент, определяемый по графику (рис. XV.30). Продольные силы влияют в основном на первый тон.