ХИМИЯ КРЕМНЕЗЕМА

Работы Одели и Эвестона

Одели и Эвестон [147] выполнили очень тщательные измере­ния молекулярной массы методами рассеяния света, ультра­центрифугирования и определения вязкости в 2,19%-ном рас - творе кремневой кислоты при рН 2,1 по мере полимеризации раствора при 24,5°С в течение 29 сут. Поскольку золь приго­товляли в щелочной среде и очищали ионным обменом, то крем­незем должен был полимеризоваться до небольших сферических частиц в течение первых суток или около того. Дальнейшая по­лимеризация в течение последующих 28 сут включает в себя процесс агрегации. Полученные данные по величинам вязкости и молекулярным массам могут быть интерпретированы с точки зрения возрастания объемной доли микрогеля и размера обла­стей микрогеля с соответствующей молекулярной массой. Это согласуется с мнением авторов, согласно которому поликрем­невая кислота не существует в растворе в виде удлиненных це­почек.

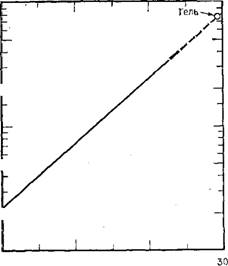
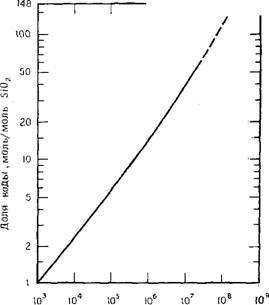
Кривые на рис. 3.40 и 3.41, полученные на основании дан­ных Одели и Эвестона, показывают повышение со временем гра­ничной вязкости nsp/C. Из них подсчитывалась доля лишенной подвижности воды, содержащейся внутри полимера или микро­геля. Вязкость, рассчитанная из уравнения Муни, быстро по­вышается, по мере того как объемная доля дисперсной фазы приближается к 0,5, т. е. к моменту, когда половина объема жидкости будет занята микрогелем. Тогда в 2,19%-ном золе кремнезема с общим молярным отношением Н20 : Si02, равным 148: 1, гелеобразование должно происходить, когда это отноше­ние в фазе геля станет 74 : 1. Из рис. 3.41 видно, что усреднен­ное значение молекулярной массы при данном отношении со­ставляет приблизительно 4-Ю7. С другой стороны, из графика, представленного на рис. 3.40, видно, что граничная вязкость в точке гелеобразования равна 0,75, а из кривой, полученной указанными авторами (рис. 7 в [147], не приведенный в на­стоящей монографии), такая вязкость соответствует молекуляр­ной массе 108, что находится в хорошем согласии с приведен­ным выше значением молекулярной массы.

При достижении точки гелеобразования соответствующая молекулярная масса отражает размер единичных образований микрогеля. Молекулярная масса, равная 108, соответствует ча­стице микрогеля, содержащей 1,7-Ю-16 г Si02. Поскольку ми­крогель содержит 2.19 Si02 и имеет плотность 1,01 г/см3, то диа­метр средней частицы микрогеля составляет, по расчету, 0,27 мкм.

Размер исходных частиц кремнезема может быть оценен из данных по начальной «гидратации» кремнезема, равной, как было сообщено, 1,8 НгО/БЮг. В рассмотренном выше разделе по вязкости золей, состоящих из очень малых частиц, было по­казано, что полное содержание связанной воды на дискретных частицах (как сумма силанольных групп и воды, связанной во-

Дородной связью) определяется размером частицы следующим образом:

36, 9сР 3,21

№0: S1O2

\\,ЫЪ D

Где d — диаметр частицы, нм.

Подставив Н20 : Si02= 1,8, получим диаметр d=l,8 нм. Степень полимеризации, равная 11,5d? или 65, соответствует молекулярной массе 3900. Это значение сопоставимо со значе­нием 5000, полученным прямым измерением.

Граничная вязкость золя nsv\C связана с усредненной моле­кулярной массой Mw полимера, полученного посредством агре­гации, следующим соотношением:

= 1,74-10"3 М0/90

Это соотношение и значительное линейное возрастание со временем величины логарифма граничной вязкости в настоящее время не могут быть удовлетворительно объяснены в рамках теории процесса агрегации частиц, происходящего в растущих областях микрогеля. Очевидно, что частицы микрогеля не яв­ляются однородными по своему размеру, как принималось выше, а имеют некоторое распределение по размерам, как это показали Одели и Эвестон методом центрифугирования. Таким образом, математическое описание подобной системы предста­вляется очень сложным.