ВЫСОКОПРОЧНЫЙ БЕТОН

ПРОЧНОСТЬ И ДЕФОРМАЦИИ БЕТОНА

Прочность бетона определяется в основном величиной соотношения количества воды и цемента по весу в исходной

/ В

Бетонной смеси и активностью цемента R ц. Закон водо-

Цементного отношения подтверждается широким диапазоном

Изменения В/Ц, примерно начиная с д = 0,25. Прочность

Бетона на портландцементе при этом может достигать Rc х « 1500-И700 кГ/см2 на сжатие и /?р = 60ч-70 кГ/см2 на растяжение. Можно считать, что для большого диапазона прочностей и цементов эта связь выражается в виде (1.1).

Формулы подобного типа имеют тот недостаток, что в них входят лишь начальные параметры бетонной смеси и в самом общем виде. Они не содержат характеристик структуры новых образований и тех параметров, которые определяют процессы их создания.

В последнее время предлагается оценивать прочность бетона с учетом физико-химических параметров структуры цементного камня.

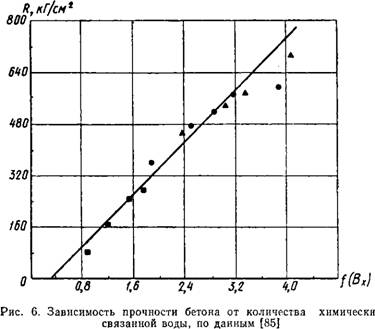
Принимается, что прочность бетона определяется при­веденной прочностью кристаллического сростка, которая в свою очередь связана с пористостью гидратных обра­зований [56]. При построении формулы прочности, основан­ной на учете разности объемных весов гидратных новооб­разований, учитывается количество химически связанной воды. При оценке прочности по концентрации новообразо­ваний в данный момент времени ( метод разработан в Харь­ковском Промстройниипроекте М. И. Стрельниковым,

Я. И. Табачишиным и М. В. Полетиком [85]) концентра­цию новообразований вычисляют с учетом количества хи­мически связанной воды, объема пор, минералогического состава цемента и В/Ц бетонной смеси. Авторы показывают, что прочность цементного камня из различных цементов, затворенных разным количеством воды, является линейной функцией количества связанной воды (рис. 6). Связь между

Пористостью цементного камня и характеристиками проч­ности и деформативных свойств бетона исследовалась так­же в работах С. В. Шестоперова [71]. При дальнейшем проведении исследований в указанном направлении необ­ходимо учитывать, что ни в одной из формул для оценки прочности затвердевшего бетона не отражен процесс раз­рушения. Между тем показано [7, 8, 10, 135], что разру­шение бетона как материала начинается с микроразруше­ний, которые затем развиваются и приводят к потере несу­щей способности конструкции.

Было бы желательно прочностные характеристики оп­ределять из уравнения деформаций материала под нагруз-

Кой. Однако пока не удается найти удовлетворительной решения этой задачи. Например, Е. Рейниус [180] пред­лагает рассматривать материал как сложную статически неопределимую пространственную решетчатую систему, в которой под действием нагрузки постепенно разрушаются связи между узлами решетки. В этом случае мы получаем аналитические зависимости между деформациями и воз­никающими напряжениями, которые совпадают с наблю­даемыми экспериментально. Модель Е. Рейниуса, конечно принципиально, правильно отражает процесс, который про­исходит в материале, но сильно упрощает его.

Учитывая постепенный характер разрушения бетона под нагрузкой сжатия, можно объяснить изменение проч­ности бетона в зависимости от скорости возрастания на­грузки, так как это связано со скоростью развития разру­шений. При больших скоростях возрастания внешней на­грузки процессы микроразрушений запаздывают, что по­вышает величину нагрузки, соответствующей стадии раз­рушения. При длительной выдержке нагрузки прочность снижается за счет того, что микроразрушения проходят с очень малой скоростью [113].

Связь деформативных и прочностных свойств бетона, как и всякого другого материала, отражается в диаграмме сжатия или растяжения. Для функциональной связи между а и є были предложены многочисленные формулы [125]. Недостаток большинства формул состоит в том, что в них не учитывались конкретные свойства материала и связы­валась только продольная деформация Єї с наибольшим нормальным напряжением а4. Между тем свойства бетона наиболее отчетливо проявляются при анализе его объемных деформаций.

Сложность анализа состоит в том, что обе упругие ха­рактеристики бетона, принимаемые в механике сплошных сред в виде констант (коэффициент Пуассона і и модуль уп­ругости £б), изменяются в процессе нагружения, и закон объемного деформирования с некоторых уровней напря­жений все больше отличается от закона упругого изме­нения объема материала, определяемого уравнением

E=s3a,(l-2|i)t (П1)

Еб

Где af — среднее нормальное напряжение, равное 1/3(сгі +

+ о2 +

GЗ) 0 — объемная деформация в окрестности данной точки, равная 0 = єі + е2 + е3.

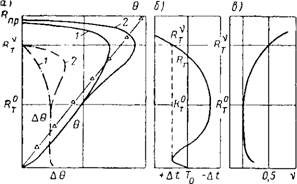
Характерные для бетона диаграммы объемного дефор­мирования при сжатии (рис. 7, а) свидетельствуют о том, что при возрастании нагрузки выше определенного предела экспериментальные данные перестают отвечать закону уп­ругого изменения объема.

Для построения диаграммы сжатия следует пользоваться такими уравнениями, которые отражали бы также законо­мерности изменения объема образца, коэффициента по­перечной деформации и модуля упругости.

Для выражения связи между наибольшим напряжением <?! и деформацией єі могут быть по предложению Г. Г. Со- ломенцова использованы уравнения вида:

Ві=в|*МЛі). (ІІ.2)

Где — соответствующая предельная деформация бе - тона на стадии разрушения; Ї|І = ^ относительная ве­личина напряжения; Rnр — призменная прочность.

Для продольной деформации уравнение, например, имеет вид

Ч= від h Ы = 8! R [ 1 — (1 - Tll)m],

А для поперечной деформации

Следовательно, объемную деформацию можно выразить в виде:

Є ^Єі+ 2єа= eli? [ 1 _(1 —п)-] + 2Є2Л [І — (1—

(И. З)

В этих уравнениях для тяжелого бетона п = т8, где

Макс*

(И.4)

В этом выражении для наибольшей прочности цемент­ного бетона (#куб = 1700 кГ/см2) следует принимать ве­личину призменной прочности #макс = 1350 кГ/см2.

Величины предельной продольной деформации сжатия могут быть установлены по эмпирической формуле (V.19), предложенной Г. Н. Писанко.

В зависимости от соотношения интенсивности развития продольных и поперечных напряжений объем образца может изменяться по двум кривым (кривые 1 и 2 на рис. 7, а). Физический смысл процессов, выражаемых обеими кри­выми, пока не ясен.