ВЫСОКОПРОЧНЫЙ БЕТОН

ПРОЧНОСТЬ БЕТОНА ПРИ МНОГОКРАТНОМ НАГРУЖЕНИИ

Установлено, что относительный предел выносливости бетона при растяжении и изгибе примерно такой же, как и при сжатии [45]. Это обстоятельство нашло свое отра­жение в существующих нормативных документах (СНиП П-В. 1-62*, СН 365-67 и др.).

В отличие от классического определения предела вы­носливости, вошедшего в литературу [45, 72], мы считаем, что под пределом выносливости следует понимать среднее максимальное напряжение стмакс, которое вызывает раз­рушение образца при базовом числе циклов[1]. Такая фор­мулировка представляется более правильной, поскольку она согласуется с общепринятым методом расчета конст­рукции по предельным состояниям, когда нормативное сопротивление при любом виде нагружения (статическом, многократном и т. д.) соответствует стадии разрушения, а запас прочности в конструкции или сооружении обеспе­чивается применением раздельных коэффициентов запаса прочности.

Предел выносливости высокопрочных бетонов зависит от следующих факторов:

1) условий загружения;

2) свойств материала;

3) условий его приготовления;

4) размеров образца и т. д.

К первой группе факторов относятся: режим нагружения (характер кривой нагружения, изменение уровня макси­мального напряжения огмакс в процессе пульсации, чере­дование многократно повторного нагружения с отдыхом и т. п.), уровень максимальных напряжений, характеристи­ка цикла р, частота приложения нагрузки.

Ко второй группе можно отнести влияние прочности образца на относительный предел выносливости, В/Ц, ко­личества цемента, состава бетона, вида и качества запол­нителя и т. п.

Выносливость Высокопрочного бетона, Как и прочность при однократном статическом нагружении, изучалась при простейших видах деформации: сжатии, растяжении и из­гибе. Исследования показали, что характер кривой нагру­жения [146], частота приложения нагрузки в диапазоне 10—103 циклов [8,146] существенно не влияют на предел выносливости. Практически мало влияют В/Ц и количество цемента [146]. Еще недостаточно изучены роль заполнителя, масштабного фактора, влияние отдыха и многократного нагружения, предварительного обжатия статической на­грузкой, изменение уровня нагружений <тмакс в течение базового числа циклов нагружений [42] и т. д. Вместе с тем установлено, что существенно изменяет предел вы­носливости число циклов нагружения и уровень макси­мальных напряжений, а также характеристика цикла р, на основании чего найдены корреляционные связи:

§2-=F(N) и - за =/(р),

Где RB — предел выносливости бетона; N — число циклов нагружения; р = характеристика цикла.

Амакс

Довольно противоречивы данные о влиянии прочности бетона на его предел выносливости. О. Я. Берг, Т. С. Ка - ранфилов, Ю. С. Волков [9, 42] считают, что с увеличением /?Пр относительный предел выносливости возрастает. О. Граф и др. [146, 81] полагают, что он не только не ме­няется, а даже уменьшается.

Поэтому, прежде чем переходить к оценке выносливости высокопрочного бетона, необходимо уточнить, как влияет изменение прочности на относительный предел выносли­вости бетона, т. е. установить имеется ли корреляционная связь

JRB Rnp

И насколько она существенна.

Т. С. Каранфилов и Ю. С. Волков [42] установили, что между выносливостью и прочностью бетона имеется хотя и слабая (коэффициент корреляции равен 0,37) корреля­ционная связь, причем с ростом прочности бетона относи­тельный предел выносливости увеличивается. Однако при этом они не использовали опытных данных, полученных при различных характеристиках цикла р и «приведенных»

12 — Фролова [101]

Лов определяли по корреляционным прямым. Полученные таким образом пределы выносливости для бетонов различ­ных прочностей при разных значениях р показаны на рис. 27, из которого следует, что в наиболее широком диа­пазоне прочностей (і? пр = 150ч--700 кГ/см2) исследованы пределы выносливости при р^ 0,1 и 0,1 <р^0,2. Для этих случаев получены корреляционные прямые, урав­нения которых имеют вид:

= 0,60— 0,00005ЯПР (Р<0,1); (IV. 1) пр (0,1 <р <0,2), (IV.2)

Т. е. для р ^ 0,1 с ростом прочности относительный предел выносливости уменьшается, для 0,1 < р < 0,2 он увели­чивается.

Однако оба вида корреляционных связей чрезвычайно слабые: в первом случае коэффициент корреляции равен 0,14, во втором — 0,27. При других значениях р не пред­ставляется возможным провести корреляционные прямые.

Таким образом, анализ опытных значений р для цен­трально сжатого бетона не дает однозначного ответа на по­ставленный вопрос. При одних значениях р относительный предел выносливости несколько уменьшается с ростом прочности, при других значениях растет. В обоих случаях коэффициенты корреляции очень малы, что свидетельствует

О слабой связи ~ = F(RnР).

Р R

К анализу функции = F(RUv) можно подойти и с

Других позиций, рассматривая механизм усталостного раз­рушения на основе данных, полученных при статических ис­пытаниях. Как уже отмечалось выше (см. главу II), при раз­рушении образца статической нагрузкой существенно важ­ными характеристиками являются параметрические точки R? и Rr> определяющие уровень микротрещинообразования бетона. Доказано, что чем выше граница микроразрушений тем больше статическая прочность образца, и что от - R0

Ношение возрастает с увеличением прочности бетона.

"пр

Можно предполагать, что процесс усталостного разру­шения начинается после первого загружения образца. При стмакс > І?? повторное нагружение вызывает даль­нейшее развитие уже появившихся микротрещин и обра­зование новых микроразрушений, связанных с преодоле­нием сопротивления усталости в отдельных точках~образца. При определенном количестве нагружений в зависимости

От соотношения образовавшиеся микротрещины сли-

RT

Ваются в макротрещины, которые затем прорастают в одну сплошную трещину, пересекающую сечение образца и вы­зывающую его разделение на части, т. е. разрушение.

Рассматривая механизм разрушения с этих позиций, надо полагать, что существует абсолютный предел выносливости бетона, равный или несколько ниже RT (так как при сгмакс = = RT при первом нагружении структура бетонного образца не нарушается), что первые микроразрушения появятся спустя большое количество циклов нагружения и что мо­мент разрушения будет значительно отдален. Так, по дан­ным [42], при нагружении образца до напряжений амакс = == до 36 • 106 циклов не началось усталостное раз­рушение, что подтверждает выдвинутую гипотезу.

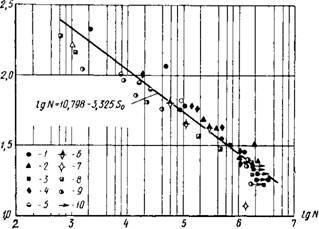
Основываясь на этом же механизме разрушения, можно сделать вывод о росте относительного предела выносли­вости с увеличением RT. Такой вывод подтверждается опыт­ными данными Г. С. Галузо по аглопоритобетону (рис. 28).

)

Аглопоритобетон на кварцевом песке: 1-R =200 кГ/см2; 2 — R =256 кГ/см2; 3-Я =323 кГ/см2; 4-ДПр=314 кГ/см2; 5-ЯПр=326 кГ/см2 5-^=451 кГ/см2] 7 —487 кГ/см2; 8 — #пр = 431 кГ/см2; то же, на агло - поритовом песке; 9 — і^Пр=326 кГ/см2 тяжелый бетон на гранитном щебне; 10 — образцы, не разрушившиеся при воздей­ствии многократно повторяющейся нагрузки

При р = 0,15 и количестве циклов N = 2-Ю6 получаем отношение

— = 1,35 ^ .

^пр ^пр

Поскольку оно увеличивается с ростом прочности, должно

RB

Возрасти и отношение при заданном р.

Апр

К сожалению, последний вывод для тяжелого бетона при разных р не доказан. Прямой анализ опытных данных, приведенный выше, лишь указывает на слабость и противо­речивость корреляционных связей между относительным пределом выносливости и прочностью бетона.

В связи с этим целесообразно установить зависимости

§±=f(N) И р)

^пр 'мір

С учетом экспериментальных данных, полученных при изуче­нии бетонов различных прочностей, и применить их к высоко­прочным бетонам.

Корреляционная связь = F(N) для бетона в полу-

^пр

Логарифмической системе координат обычно представляется в виде кривой линии:

^-^A—blgN. [(IV.3)

#пр

Такое выражение при значениях N = 103-f-107 хорошо согласуется с опытными данными и возражений не вызывает. Продолжение прямой выносливости влево до пересечения с осью ординат, по данным [83], приводит к тому, что при

N = 1 отношение меньше единицы, что невозможно

Апр

Объяснить с позиций физики твердого тела.

В том случае когда прямая продолжена вправо до пере­сечения с осью абсцисс, приходится признать, что при ко­нечном числе циклов образец должен разрушиться при амакс ^ О» что невозможно. В литературе уже обращалось внимание на то, что линия выносливости бетона в полуло­гарифмических координатах не является прямой [42, 72].

Анализ выносливости центрально сжатого бетона пока­зывает, что в полулогарифмических координатах функция

D

= /(lgN) действительно криволинейна. Для р^0,1 уравнение такой кривой можно записать в виде:

— = l,23N-°'05. (IV.4)

Япр

Из уравнения (IV.4) следует, что при N = 1 отношение

D

■5і = 1,23, а к оси абсцисс кривая асимптотически при-

Ближается при NОо. Из рис. 29 видно, что она удов­летворительно согласуется с опытными данными.

Рис. 29. Изменение относительного предела вынос­ливости Яв/Япр в зависимости от числа циклов на­гружения N, по данным

/—Антрима и Лафлина [114]; 2 — Беченевой [21]; 3 — Гама - юнова; 4 — Каранфилова и Волкова [42]; 5 —Карпухина [45]

Рис. 30. Прямые выносливости в логарифмической системе

Координат, по данным

А — Каранфилова и Волкова [42]; б— Карпухина [45] и в—Антрима и Лафлина [114]

Данные [42, 45, р ^ 0,1 отношение

Р

Чине отношения Q-^-ПрИ N = 1.

Апр

Т. С. Каранфилов и Ю. С. Волков отмечают [42], что при

D

N = 1 отношение должно

Апр

Быть больше единицы, так как скорость загружения влияет на прочность бетонного образца. Г. В. Беченева [21] показала, что при нагружении образца за 0,4—2 сек прочность на сжатие возрастала примерно на 20% по сравнению с прочностью при обычном испытании. Поскольку испытания на выносливость обычно осуществляются при вы­сокой скорости нагружения (ча­стота 5—10 гц)у то естественно,

П

Что отношение q-~ при N = 1

Апр

Должно быть больше единицы. На рис. 30 показаны опытные из которых следует, что при

При N = 1 колеблется от 1,17

Выносливость с большой скоростью прикладывается лишь величина напряжений, равная амак

Рассмотрим корреляционную связь = /(р). Известно,

^пр

Оказывает существенное влияние на

*L

Rnv 1,0

И VT Hfi dji Ifip

Предел выносливости бетона, причем с уменьшением р он снижается. По данным различных авторов, функция =

^пр

= /(р) оценивается по-разному (рис. 32). Средние значения 1,0

Пределов выносливости высокопрочного бетона на базе 2 млн. циклов удовлетворительно согласуются с зависи­мостью (рис. 33):

=0,35р2+ 0,60.

#пр

Из формулы (IV.5) следует, что при р = 0 предел вы­носливости получается равным 0,6 і? цр, а при р = 1 — —0,95 /?ир.

(IV.5)

Большинство авторов считают, что при р == 1 предел выносливости должен быть равен «длительной прочности бетона», не поясняя, к какому времени нагружения отно­сится понятие «длительная прочность». В работах [9, 45] эта величина принимается равной 0,85 /?пр.

П

Отношение -5і - при р = 1 можно объяснить основываясь

^пр

На следующих соображениях. При высоких значениях р (например, р = 0,99) несущую способность образца при базовом числе циклов 2 млн. можно рассматривать и как предел выносливости при р = 0,99, и как длительную проч­ность при времени загружения образца, равном времени создания базового числа циклов. Это возможно потому, что при р = 0,99 многократно прикладывается лишь незначи­тельная часть напряжения, равная сгмакс — сгмин = 0,01амакс. При р = 1 напряжения к образцу приложены статически, однако для сравнения со всеми предыдущими случаями (р = 0,9; 0,99; 0,999) логично принять, что время нагру­жения образца остается одним и тем же, т. е. равным вре­мени для создания базового числа циклов. Тогда при р = 1

П п

Отношение -5і - заменяется отношением - к35-, где /?дл —

*<пр Апр Л

Длительная прочность образца при времени нагружения, равном времени создания базового числа циклов. В этом случае предел выносливости при р = 1 и базовом числе циклов 2 млн. [формула (IV.5)] можно рассматривать как длительную прочность при времени загружения 2—4 суток (частота 10—5 гц). Если увеличить базу испытаний до 10 млн. циклов, предел выносливости при р = 1 должен понизиться и будет меньше 0,95 /?пр, т. е. величины, ко­торая получается при расчете по формуле (I V.5).

Следовательно, корреляционные связи, существенно влияющие на предел выносливости бетона, могут быть при­няты в соответствии с зависимостями (IV.4) и (IV.5), которые удовлетворительно согласуются с опытными дан­ными.

Относительный предел выносливости для высокопроч­ного бетона при р ^ 0,1, вычисленный по формуле (IV.5), равен 0,6. Коэффициенты /Ср, представляющие собой от­ношение пределов выносливости при р>0,1 к пределам выносливости при р ^ 0,1, могут приниматься следующие: