ВОЗОБНОВЛЯЕМЫЕ ИСТОЧНИКИ ЭНЕРГИИ
Функции состояния
Состояние заданного количества идеального газа полностью оп - тяется любыми двумя из трех переменных: давлением, объемом, темпера - ій. Третья переменная может быть вычислена, если заданы две другие пере - ■гнные (при условии, что известно количество газа, выраженное в киломолях), уравнения состояния идеального газа.
Если газ переходит из одного состояния в другое, то можно вычислить из - ение его внутренней энергии. Для того чтобы это сделать, достаточно знать К'ство газа, его удельную теплоемкость при постоянном объеме, а также іьную и конечную температуры. При этом неважно, как менялась темпера в процессе перехода газа из одного состояния в другое.
С другой стороны, для того чтобы вычислить работу, совершенную при Пеле из одного состояния в другое, важно точно знать, по какому пути был ршен рассматриваемый переход. Знания только начального и конечного • эяний в этом случае недостаточно. В эксперименте, описанном выше,
,
а, совершенная при переходе в конечное состояние, зависела от того, ,'М образом протекал процесс. Никто не может сказать, какую работу надо шить для того, чтобы перейти из одного состояния в другое, опираясь ‘ ко на знание этих состояний. Если Вы увидели кого-то на вершине горы, Ьы не можете знать, каких усилий стоило это восхождение. Можно выбрать «>ю. вымощенную дорогу, а можно пойти длинным усеянным камнями Другими словами, работа не является функцией состояния газа.
2.12. ЭНТАЛЬПИЯ
До сих пор мы имели дело только с замкнутыми системами, в которых рассматривалась некая фиксированная масса газа. Многие устройства, например, такие как турбина, являются открытыми системами, через которые проходит поток газа. Вместо того, чтобы фиксировать свое внимание на заданной массе газа, мы должны рассматривать заданный объем, через который проходит поток газа, претерпевающий некоторые термодинамические изменения. Для того чтобы вычислить изменение энергии, происходящее в такой открытой системе, мы должны вычислить энергию, приносимую в нее потоком, и энергию, уносимую из нее.
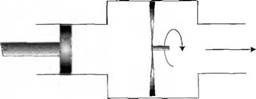
Для того чтобы создать поток в открытой системе, изображенной на рис. 2.3, представим себе некий (воображаемый) поршень, создающий давление р и проталкивающий объем газа V через наше устройство. Поршень создает силу рА и, толкая газ, перемещается на расстояние L, совершая при этом работу pAL = pV. Энергия, вводимая в устройство, равна рвх Vm. На выходе из устройства газ уносит энергию, равную РВЫХУВЫХ. Тогда энергия, накопленная в устройстве, равна Рвх Кх ~ Рвых Кык - Если при этом газ изменил свою внутреннюю энергию, то полная работа, совершенная устройством, выражается как
W = A(pV) + AU = A(pV+ U)= АН. (62)
Предполагается, что устройство является адиабатическим (т. е. нет теплообмена с внешней средой через стенки устройства).
|
Рис. 2.3. Открытая система, в которой поток газа совершает работу |
Сумма pV + Uчасто используется в термодинамике, и определяемая с ее помощью величина называется энтальпией
Н = U + pV. (63)
Величины И, U и pV, будучи энергетическими характеристиками, являются относительными, т. е. они могут быть отсчитаны от некоего произвольного уровня. Их абсолютные значения не столь важны. Наибольший интерес представляет изменение этих величин:
АН = AU = A(pV) = AU + pAV + VAp. (64)
При постоянном давлении АН есть просто AU + рАУм, следовательно, равно теплу Д Q, которое вводится в систему,
АН = AU + pAV = AQ. (65)
По этой причине энтальпию иногда называют теплосодержанием. Эта величина, как правило, используется в химии, потому что зачастую реакции протекают в открытых сосудах, т. е. при постоянном давлении.
Из уравнения (12) следует (в расчете на 1 кмоль)
т
AU=]cvdT (66)
То
Используя уравнение состояния для идеального газа (также на 1 кмоль) и шнение (64) получаем
АН = AU + A{pV) = AU + A(RT)= j cvdT + Rj dT = j (cv ^ R)dT = j cpdT.
To? o Г0 T„
(67)
Сопоставьте уравнения (66) и (67).