ВОПРОСЫ ТЕОРИИ. И ИННОВАЦИОННЫХ РЕШЕНИЙ. ПРИ ИСПОЛЬЗОВАНИИ. ГЕЛИОЭНЕРГЕТИЧЕСКИХ СИСТЕМ
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В ГЕЛИОСИСТЕМЕ В КВАЗИСТАЦИОНАРНОМ РЕЖИМЕ
Рассмотрим математическую модель тепловых и гидродинамических процессов, происходящих в солнечной нагревательной системе, состоящей из солнечного коллектора, бака аккумулятора и соединительных трубопроводов - подъемного и опускного. Тепловой расчет всех элементов солнечной системы с естественной циркуляцией теплоносителя может быть выполнен на основе математической модели, учитывающей наиболее существенные факторы тепловых и гидродинамических процессов, происходящих в каждом из элементов системы при их взаимодействии. Такая модель может быть представлена нестационарными уравнениями теплопроводности для каждого элемента установки, а также уравнением движения жидкости, циркулирующей по термосифонному контуру. В разработанную математическую модель был внесен ряд изменений и дополнений по сравнению с известными решениями [50]:
- модель базируется на двумерном представлении тепловых процес-сов с учетом теплоемкости материалов, что особенно важно для случая использования полимеров в конструкции солнечного коллектора;
- учитывался эффект охлаждения абсорбера солнечного коллектора жидкостью, поступающей из бака-теплоаккумулятора.
Для упрощения этой модели воспользуемся методами теории размерностей. Дифференциальная задача приводится к безразмерному виду. В качестве характерных (масштабных) величин принимаются следующие значения: время начала работы системы т0 = 10 ч 00 мин; размер - длина соответствующего элемента системы 10; средняя температура элемента системы Т массовый расход жидкости G0, соответствующий 12 ч 00 мин.
При тепловом расчете водонагревательной системы для уравнений теплопроводности прозрачного покрытия, теплоприемника и жидкости в каналах коллектора и трубопроводах можно использовать стационарные приближения, в то время как для бака-аккумулятора рассматриваемой системы, распределение температурного поля по высоте аккумулируемой емкости с течением времени должно описываться нестационарным уравнением. Таким образом, математическая модель рассматриваемой гелиосистемы в квазистационарном приближении представляется следующей дифференциальной задачей:
1) для прозрачного покрытия:
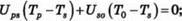
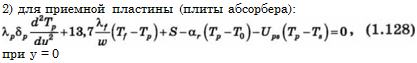 |
(1.127)
![]() (1.129)
(1.129)
3) для жидкости в трубах коллектора:
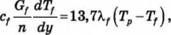 (1.130)
(1.130)
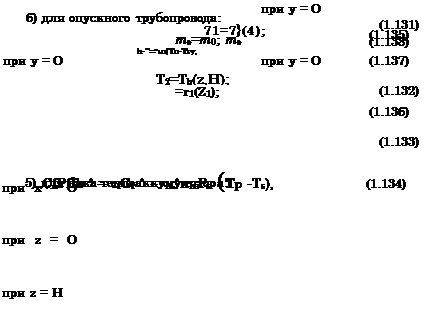 |
7) уравнение движения жидкости в каналах абсорбера:
ik
kfGf=gv0sinQkj(Tf(y)-T2(l2))dy. (1.139)
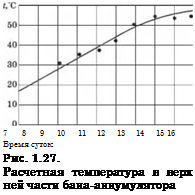
В соответствии с разработанной моделью был проведен расчет гелиосистемы с плоским солнечным коллектором. Для трубопроводов и бака-теплоаккумулятора (БТА) длина подающего трубопровода 1х = 1 м; длина отводящего трубопровода 12 = 2 м; диаметр трубопровода = d2 = 0,025 м; высота БТА - Н = 0,6 м; диаметр емкости БТА - d6 = 0,46 м.
Результаты расчетов представлены на рис. 1.26 и 1.27. Точками показаны экстремальные данные.
![]()
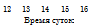
 Gf, кг/с 0,018 0,016 0,014 0,012 0,010 0,008 0,006 0,004 0,002 0
Gf, кг/с 0,018 0,016 0,014 0,012 0,010 0,008 0,006 0,004 0,002 0

