ВОПРОСЫ ТЕОРИИ. И ИННОВАЦИОННЫХ РЕШЕНИЙ. ПРИ ИСПОЛЬЗОВАНИИ. ГЕЛИОЭНЕРГЕТИЧЕСКИХ СИСТЕМ

ИСПОЛЬЗОВАНИЕ ТЕПЛОВЫХ ТРУБ

Один из путей энергосбережения при передаче и транс­формации тепловых потоков заключается в применении тепловых труб, которые характеризуются рядом преиму­ществ: низким термическим сопротивлением, не требуют дополнительных затрат энергии на передачу теплоносите­ля [89].

В работе [90] для оптимизации тепловых труб вводятся функции

2'nqXx-[klht1X + k2At2(L-X)]x
Tip X(L-X)r2

где f1 - изменение КПД жидкой фазы на единицу длины X; /2 - относительная энергия, выработанная генератором фа­зового перехода; г - радиус тепловой трубы; q - плотность теплового потока; X - участок трубы, куда подводится по­ток солнечной радиации; kv k2 - коэффициенты теплопе­редачи соответственно через участки X и L - X тепловой трубы; Atx = £ж - tH - разность температур жидкости и на­ружного воздуха; At2 = tn - tH разность температур пара и наружного воздуха; L - длина тепловой трубы; т - время; р - плотность; А, - удельная теплота испарения.

Оптимальный тепловой режим при условии 8f2/de = 0 описывается зависимостью

% = 2Ь/а, (1.221)

где ^ = X/L; & = [ft1At1X + ft2At2(L-X)]x; а = 2nrqXi.

Величина £, связана с f2 зависимостью

/2 = (а$-в)/ф$а), (1.222)

где D = npX(L - X).

Надо признать, что, невзирая на ряд существенных преимуществ, тепловые трубы в качестве теплообменных аппаратов не нашли должного применения в сельском хо­зяйстве. Несомненно, что технико-экономически обосно­ванное использование тепловых труб в системе энергоснаб­жения сельского хозяйства окажется весьма эффективным.

Методам расчета и выбора оптимальных параметров те­плообменных аппаратов на тепловых трубах посвящен ряд работ, среди которых следует выделить [91-94]. Заслужи­вает внимания методика теплотехнического расчета тепло­обменников на тепловых трубах, изложенная в работе [95].

При проверечном расчете задают температуру на входе и выходе холодного теплоносителя t10, tl2; расход горячего

И ХОЛОДНОГО теплоносителей Gj и G2; схему движения пото­ков. Требуется определить: поверхность теплообмена в го­рячей и холодной зонах аппарата Fv F2; его эффективность Е; число рядов и количество тепловых труб; характеристи­ки оребрения.

При проверочном расчете известны количество зам­кнутых испарительно-конденсационных контуров, их тип, число рядов, схема движения потоков, Fv F2, tw, t20, Gv G2. Необходимо определить суммарный тепловой поток, зна­чения температур теплоносителя на выходе из теплообмен­ника tln, t2n.

Соотношение для определения температуры насыще­ния в і-й тепловой трубе имеет вид

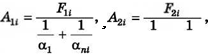(1.223)

где tu и t2i - локальные температуры греющего и нагревае­мого теплоносителей; Fu, F2І - поверхности теплообмена в і-й тепловой трубе в зонах нагрева и охлаждения соответ­ственно; oij, апі - коэффициенты теплоотдачи с наружной и внутренней сторон тепловой трубы в зоне нагрева; а2, аы - коэффициенты теплоотдачи с наружной и внутренней сто­роны тепловой трубы в зоне охлаждения.

Тепловой поток, передаваемый через і-ю тепловую тру­бу, определяется из соотношения

Qi = Iі ~ . (1.225)

Ац Аїі

Если принять обозначение

' 1 1

----- +

Аі у

где Кы имеет смысл коэффициента теплопередачи, отнесен­ного к одной тепловой трубе, то уравнение (1.225) можно записать следующим образом:

Закон распределения температуры насыщения по ря­дам тепловой трубы имеет вид:

tsi = {*10 Iі - еХР(- тКш 0 +

+ [ 1 + (W2 /Wl) exp (-тКаі і)] + t2о [(W2/Wl)e^p(-mK3i і) + (1.228)

+ z, [(W2 jWx)exp(-тКві і)] } [(1 + W2/Wx )(2l + l)]'1

где Wl = GjCpl; W2 =G2cp2; m = —— + —— ; Gx и cpl - рас­ход И удельная (j1cpl (-*2Cp2

изобарная теплоемкость греющего теплоносителя; G2 и ср2 - расход и удельная изобарная теплоемкость нагревае­мого теплоносителя.

Уравнение (1.225) справедливо при постоянстве значе­ний т, Kgi, Wv W2 и z.. Такое предположение вполне допу­стимо для незначительных перепадов температур, что, как правило, характерно для процессов теплообмена, имеющих место в сельскохозяйственных технических устройствах.

Рассмотрим задачу оптимизации теплообменных аппа­ратов с тепловыми трубами.

Эффективность таких аппаратов в значительной степе­ни зависит не только от внешних условий теплообмена, но и от параметров тепловых труб, используемых в них.

Выбору оптимальных параметров должно предшество­вать определение целевой функции. При этом основными являются требования обеспечения минимума материаль­ных затрат и энергопотребления, или, в общем случае,
рентабельность приведенных затрат. Задача заключается в том, чтобы добиться минимальной массы, приходящей­ся на единицу передаваемой теплоты m/Q и минимальных удельных затрат N/Q на прокачку теплоносителя.

С увеличением расхода теплоносителя возрастает ко­эффициент теплопередачи. Вместе с тем, возрастание расхода теплоносителя повышает необходимую мощ­ность для его прокачки. Следовательно, существует рас­ход теплоносителя, при котором достигается минимум энергопотребления.

Обоснованный выбор основных параметров теплооб­менных аппаратов на тепловых трубах требует постановки и решения соответствующей оптимизационной задачи, т. е. определения минимума комплексной функции вида [95]

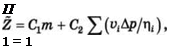(1.229)

где z - целевая функция; т - масса теплообменного ап­парата; У; - скорость движения теплоносителя; Сг, С2 - ко­эффициенты, позволяющие согласовать z с конкретным значением соответствующего критерия оптимальности. Например, если рассматривать Z, как некоторую эквива­лентную массу, то С1 = 1, а С2 - эквивалент энергозатрат на прокачивание; Ар - перепад давлений; цг - КПД; игАр/тіг - энергозатраты на прокачивание теплоносителя і.

Масса теплообменного аппарата с тепловыми трубами пропорциональна поверхности теплообмена:

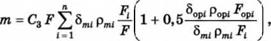(1.230)

где С3 - коэффициент, учитывающий увеличение массы те­плообменного аппарата с тепловыми трубами за счет кор­пуса, обвязки и внутрикорпусных деталей (в первом при­ближении определяется по справочным данным [93]); 8ті и рті, 8орі и рорі - толщина и плотность материала стенки

и оребрения соответственно; F0ViIFt - коэффициент оребре - ния в соответствующей зоне аппарата.

Полученную поверхность теплообмена аппарата с те­пловыми трубами можно рассчитать из известного инте­грального соотношения

f = £з=—

Н ЬА Т

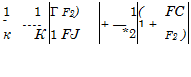
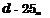
При этом следует учитывать особенности в определении коэффициента теплопередачи [96]:

где F., Fv F2 - внешние поверхности тепловых труб в со­ответствующих зонах; cl - коэффициент теплоотдачи на внешней поверхности тепловых труб в соответствующей зоне; FiB - внутренняя поверхность тепловых труб в со­ответствующей зоне; olb - коэффициент теплоотдачи на внутренней поверхности тепловых труб соответствующей зоне; d - внешний диаметр тепловых труб; А, м - теплопро­водность материала стенки.

Обобщая вышеприведенное, можем рассматривать функционал z как вектор пространства состояния системы

где St - живое сечение в соответствующей зоне. В форму­ле (1.234) F2/F1, kt, St, щ, FopijFt являются переменными функциями и независимыми параметрами х] уравнения теплообменного аппарата с тепловыми трубами. Тогда ре­шением конкретной задачи оптимизации следует считать
такое значение Х} , при котором для остальных элементов множества cij <Xt <Ц выполняется неравенство

z(x] )>г(Щ). (1.235)

Отсюда следует

г = г(Щ)^> minZ(xT). (1.236)

Qj ^ Xj ^ bj

В результате приходим к известной задаче нелинейного программирования:

£=0. (1.237)

дХ;

которая решается численными методами (Лагран­жа-Понтрягина, Гамильтона-Якоби-Веллмана и др.) [97].

Принцип максимума Понтрягина относится к зада­че оптимального управления. Наиболее полное решение этой задачи получено для линейных систем, где соотноше­ния принципа максимума Понтрягина часто выступают не только как необходимое, но и как достаточное условие оптимальности [98]. Принцип максимума Понтрягина по­лучил многочисленные обобщения в различных сложных задачах.

Теория Гамильтона-Якоби относится к вариационному исчислению, в котором нахождение экстремума функций сводится к интегрированию уравнения с частными произ­водными первого порядка [99].