ВОПРОСЫ ТЕОРИИ. И ИННОВАЦИОННЫХ РЕШЕНИЙ. ПРИ ИСПОЛЬЗОВАНИИ. ГЕЛИОЭНЕРГЕТИЧЕСКИХ СИСТЕМ
ГАЗОПРОНИЦАЕМЫЙ АККУМУЛЯТОР
По данным [34] в системе солнечного теплоснабжения перспективно применение аккумуляторов теплоты с газопроницаемым материалом. Работа аккумуляторов основана на использовании теплоты фазового перехода и хемодесорбции. Как показали опыты, особый интерес представляют порошки с преобладанием двуокиси ванадия. Фазовый переход металл-диэлектрик в этом соединении происходит с выделением теплоты (удельная теплота превращения 0,24 кДж/моль).
Характерными особенностями таких материалов являются развитая поверхность пор и, как следствие, их высокая газовая реакционная способность. Ультрадисперсные порошки обладают высокой активностью к поглощению газов (адсорбцией), в первую очередь, кислорода. Состав и количество адсорбированных порошками газов определяется природой материала, его дисперсностью и условиями приготовления. Теплообмен в таких средах происходит при наличии фазового перехода в частицах, процессов адсорбции-десорбции газа на поверхности пор, а также его хемосорбции с фазами переменной валентности.
Одной из важных проблем при изучении таких материалов является выяснение влияния механической активации поверхности частиц порошка на теплообмен.
Предлагается следующая постановка задачи. Плоский слой газопроницаемого материала нагревается внешними источниками излучения и обменивается теплотой с окружающей средой путем конвекции. Перенос теплоты в газопроницаемом материале осуществляется теплопроводностью, излучением и конвекцией. Принимается, что скорость течения газа в порах достаточно мала, поэтому устанавливается тепловое равновесие между газом и каркасом.
Необходимо учитывать существование внутренних источников теплоты за счет фазового перехода в объеме частиц и хемосорбции кислорода на поверхности пор.
При моделировании радиационного переноса также учитываются процессы поглощения, испускания и рассеивания на частицах окислов ванадия. Оптические свойства материала предполагаются зависящими от длины волны. Внешние источники излучения являются абсолютно черными. Теплоемкость каркаса предполагается зависящей от температуры.
Решение задачи проводится в приближении сплошной среды с эффективными теплофизическими и оптическими свойствами. Температурные поля и тепловые потоки в слое материала получаются из решения краевой задачи для уравнения теплопроводности и системы уравнений переноса излучения.
Уравнение теплопроводности с граничными условиями в безразмерном виде:
![]()
![]()
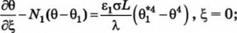
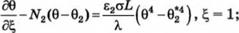 сЯ=д_дв'
сЯ=д_дв'
дх 8^ ч
(1.67)
(1.68)
|
![]()
![]() LgcT Т х
LgcT Т х
—L; 0=—; ^=—; т = 1 - Р Г* L
Расход газа в порах рассчитывается из уравнения неразрывности
P-| = L/7v(0). (1.70)
db,
Дивергенция спектральной плотности радиационного потока dE/d^ определяется из решения системы интегро - дифференциальных уравнений переноса энергии излучения [34] относительно интенсивностей /*(4»р)» Iv (<;,р) и имеет вид
![]() _ 1
_ 1
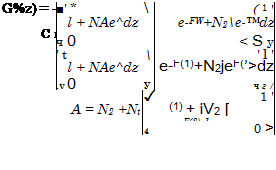 |
|
4nlpv - 271J(/; (§, р) +1~ (§, р))dp
начально-краевая задача (1.66)—(1.69) сводится к нелинейному интегральному уравнению относительно безразмерной температуры, которое записывается в виде
і
^,x) = G{^Q)W^)-G{^)W2(x) + W{z, x)G^,z)dz. (1.72)
о
Здесь
W(z, x) = ^+^-L2q(Q);
дх % dz
Ж1(т) = ^(е;4-04)-ЛГ1Є1;
Ж2(т) = ^(04-0^)-ЛГ20*4.
Таким образом, краевая задача (1.66)—(1.72) о совместном переносе теплоты теплопроводностью, конвекцией и радиацией в полупрозрачной газопроницаемой среде свелась к нелинейному интегральному уравнению относительно безразмерной температуры 0(£, т), которое на каждом временном шаге решается итерационным методом Ньютона-Канторовича [35].
Для нахождения эффективных значений коэффициента теплопроводности газопроницаемого материала использована формула
Я = (1 - Р)ХЕ + РХр.
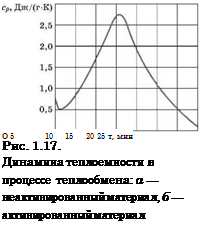
Расчеты проводились с использованием временных зависимостей теплоемкости, представленных на рис. 1.17. Эти зависимости получены путем обработки экспериментальных данных [36].
 |
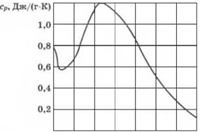 |
Прежде всего необходимо отметить наличие ярко выраженного пика в распределении теплоемкости во времени в моменты, когда в материале происходит фазовый переход. Механоактивация материала приводит к уменьшению максимального значения теплоемкости и расширению во времени пика. При проведении числовых расчетов параметры принимали следующие значения: X = 1,34 Вт/м'К, L = 0,1 м, N1 = N2 = 9,5, el = є2 = 1. Шаг по времени At принимался равным 1 с.
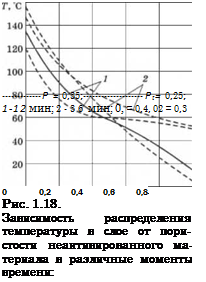
На рис. 1.18 представлены результаты расчета температуры в слое для случая нагрева границы ^ = 0 источником излучения с температурой 400 К и границы Е, = 1 источником с температурой 330 К. Из рисунка видно, что рост пористости приводит к возрастанию температуры в горячей области слоя и снижению температуры в холодной области в каждый момент времени. Снижение пористости материала приводит к увеличению внутреннего тепловыделения за счет хемосорбции и уменьшению скорости нагрева.
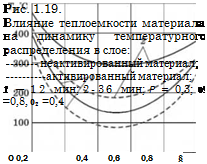
Рис. 1.19 иллюстрирует влияние теплоемкости каркаса пористого материала на температурное распределение в слое в различные моменты времени. На этом рисунке видно, что механоактивация материала приводит к дополни-
 |
 |
тельному разогреву слоя за счет тепловыделения при релаксации структуры стенок пор.