ВНУТРЕННИЕ УСИЛИЯ И ДЕФОРМАЦИИ ПРИ СВАРКЕ
Нагрев стального стержня
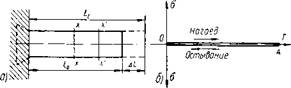
При равномерном нагреве свободного или закрепленного одним концом стального стержня (фиг. 16, а) длина его будет увеличиваться и при температуре Т станет равной
lt = /0(1 +аТ), (17)
где /о — длина стержня при 0°С;
Т — температура нагрева;
а — коэффициент линейного теплового расширения стали.
|
Фиг. 16. Нагрев стального стержня с одним свободным концом: а — стальной стержень; б — цикл нагрева и остывания в координатах а— Т. |
Ввиду отсутствия связей, препятствующих свободному тепловому удлинению волокон стержня, напряжения в нем возникать не будут. При остывании длина стержня будет уменьшаться соответственно изменению температуры. Напряжения в металле стержня не возникнут, так как связи, препятствующие свободному тепловому укорочению, отсутствуют. После остывания длина стержня будет равна первоначальному размеру /0. Процесс нагрева и остывания стального стержня можно изобразить в координатах а—Т (напряжение — температура) замкнутым циклом оЛо, совпадающим с осью абсцисс Т (фиг. 16, б). Если равномерно нагревать не весь стержень, а любое его поперечное сечение хх, или участок между двумя параллельными поперечными сечениями хх и х'х', то благодаря отсутствию препятствий. нагретые места будут свободно удлиняться подобно предыдущему без появления напряжений. Точно так же после остывания длина стержня укоротится до первоначальных размеров /0.
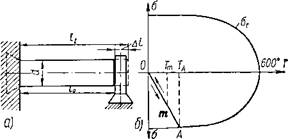
Рассмотрим нагрев стального стержня, левый конец которого закреплен в неподвижной опоре, а правый свободно касается
жесткого неподвижного упора (фиг. 17, а). При нагреве стержня от нуля до температуры Т удлинение было равно
Д/ = а770. (18)
|
|
|
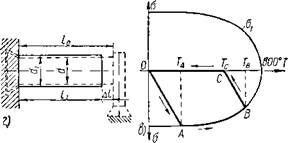
Фиг. 17. Нагрев стального стержня, ограниченного неподвижным упором: а — стальной стержень с неподвижным упором; б — изменение напряжений в стержне при температурах упругого состояния стали; в — изменение напряжений при температурах упругого и упруго-пластического состояния стяли; г — размеры стержня после остывания. |
Ввиду наличия неподвижных жестких препятствий увеличение длины стержня при повышении температуры невозможно, и
в нем возникнут напряжения сжатия, которые в пределах температур упругих изменений стали будут равны
at=^-E = аЕТ. (19)
1Ь
Согласно принятому нами ранее допущению произведение аЕ = 25 кГ/см2 и закономерность изменения напряжений сжатия в нагреваемом стержне по формуле (19) можем представить в виде
Of = clET = 25Т. (20)
Нарастание напряжений сжатия с повышением температуры стального стержня согласно формуле (20) будет происходить по прямой оА (фиг. 17, б). Кривая От представляет изменение предела текучести стали в зависимости от температуры. При тем
пературе Та напряжение сжатия достигнет предела текучести стали От - Значение температуры ТА, при которой в нагреваемом стальном стержне, ограниченном жесткими неподвижными опорами, напряжение сжатия достигнет предела текучести, найдем по формуле (19) или (20)
|
|
Если предел текучести вт = 2500 кГ/см2, то по формуле (21) значение температуры Та должно быть
= 100° С. (21,а)
В практических условиях нагрева ограничивающие препятствия обладают некоторой податливостью, и напряжение предела текучести наступает при более высокой температуре, чем 100° С.
Если ограниченный неподвижными опорами стальной стержень нагревать до температуры Тт, не превышающей значения Та (см. фиг. 17, б), то после остывания напряжения исчез - нут, а размеры стержня останутся без изменения. Процесс нагрева и остывания стержня в области температур, не превышающих значения ГА, можно изобразить в координатах а — Т циклом ото (фиг. 17, б). При нагреве того же стержня до температур, превышающих значение ТА, например, до температуры Гв, изменение напряжений сжатия с повышением температуры от Та до Тв (фиг. 17, в) будет происходить по кривой предела текучести 0т (участок АВ). В металле стержня будут протекать деформации пластического сжатия (подсадка металла) при напряжениях, равных значению предела текучести стали соответственно ее температурному состоянию.
При остывании от температуры Тв до Тс стержень освобождается от напряжений упругого сжатия вследствие, укорочения волокон. Напряжения сжатия уменьшаются по закону прямой ВС, параллельной оА (см. фиг. 17, в). При температуре Тс напряжения сжатия спадут до нуля, и правый конец стержня будет свободно касаться своего упора. Процесс дальнейшего остывания будет протекать подобно рассмотренному выше случаю остывания свободного ненапряженного стержня (см. фиг.
16, а), т. е. стержень свободно укорачивается с понижением температуры. После полного остывания объем стержня останется неизменным, а линейные его размеры, ввиду образования при нагреве деформаций пластического сжатия, изменятся. Диаметр стержня увеличится, а длина уменьшится на величину А1 (фиг.
17, г). Укорочение стержня к концу остывания равно
Д/ = а Тс10. (22)
Изменение напряжений в процессе нагрева и остывания стержня изображается, в координатах а—Т замкнутым циклом
оАВСо (см. фиг. 17, в). Таким образом, отсутствие связей, препятствующих свободному укорочению стержня при остывании, приводит к освобождению металла от остаточных напряжений, несмотря на образование пластических деформаций сжатия в процессе нагрева.
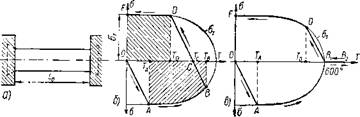
При нагреве стального стержня, который при нулевой температуре закреплен обоими концами в жестких неподвижных опорах (фиг. 18, а), в нем возникнут напряжения сжатия, которые согласно формуле (19) будут нарастать по прямой оА (фиг. 18, б). При температуре Та напряжения сжатия достигнут пре-
|
Фиг. 18. Нагрев стального стержня, закрепленного и неподвижных опорах: а — стержень с закрепленными концами; б — изменение напряжений при нагреве до температур упруго-пластического состояния стали; в — изменение напряжений при нагреве до температур пластического состояния стали. |
дела текучести От• Дальнейшее повышение температуры от ТА до Тв вызовет образование в металле стержня деформаций пластического сжатия. Изменение упругих напряжений сжатия на участке АВ будет происходить по кривой предела текучести ат - На фиг. 18, б заштрихованная площадь АТаТвВ представляет в координатах а—Т область образования пластического сжатия при напряжениях, равных пределу текучести стали соответственно ее температурному состоянию.
При остывании стержня от температуры ТА напряжения сжатия будут снижаться по прямой ВС, и при температуре Тс стержень освободится от напряженного состояния. Дальнейшее понижение температуры приведет к появлению в стержне напряжений растяжения, ввиду препятствий свободному укорочению со стороны жестких неподвижных закреплений. Эти напряжения растяжения с понижением температуры будут нарастать по прямолинейному закону упругих изменений стали (прямая CD) до достижения предела текучести растяжения при температуре TD (фиг. 18, б) . При дальнейшем остывании от температуры TD до начальной, в нашем случае до нулевой, напряжение растяжения стержня будет изменяться по кривой предела текучести (участок DF). В металле стержня будут протекать пластические удлинения при напряжениях, равных пределу текучести 0т - На фиг. 18, б область пластического удлинения стер-
Жня в процессе остывания представляет заштрихованную площадку OFDTd.
После полного остывания в стержне останутся напряжения растяжения, равные пределу текучести стали в холодном состоянии. Как видим из диаграммы на фиг. 18, б, остаточные напряжения растяжения выражаются ординатой OF, замыкающей в координатах а—Т цикл OABCDF, описывающий процесс нагрева и остывания закрепленного обоими концами стального стержня.
Усилие, вызываемое происходящими в металле закреплен* ного стержня упругими изменениями в процессе нагрева и остывания, равно
Р = ctF, (23)
где F — поперечное сечение стержня, a ot—напряжение, соответствующее температуре нагрева или остывания металла стержня. Усилие, порождаемое в закрепленном стержне под влиянием теплового цикла, уравновешивается реактивным сопротивлением концевых опор.
Остаточное усилие в рассмотренном нами случае нагрева закрепленного стального стержня равно
Р = oTF. (24)
Если после остывания стержня удалить концевые опоры, то остаточные напряжения растяжения исчезнут, а длина стержня уменьшится на величину
М = - J V (25)
На фиг. 18, в изображена диаграмма изменения напряжений при нагреве закрепленного обоими концами стального стержня до температур выше 600° С. На участке BiB2, где температура выше 600° С, согласно принятому нами допущению сталь находится только в пластическом состоянии. Поэтому напряжения в области этих температур отсутствуют. Прямая BD характеризует закономерность нарастания напряжений растяжения с момента перехода стали в упругое состояние, т. е. в процессе
остывания от температуры 600° С. Изменение напряжений рас
тяжения для этого периода остывания может быть выражено уравнением
ст = аЕ (600 — Т) = 25 (600 — Т), (26)
где переменная Т изменяется от 600°С до Тв (см. фиг. 18, в).
Так как произведение а Е в пределах упругих изменений стали принято нами постоянным и равным 25 кГ/см2, то прямая ВіД выраженная уравнением (26), параллельна прямой О А, что видно из сопоставления формул (20) и (26). При температуре TD напряжения растяжения достигнут предела текучести и при дальнейшем остывании будут изменяться по кривой ат (участок DF).
Цикл нагрева и остывания OABiB^BiDF (фиг. 18, в) замыкается ординатой OF, представляющей остаточные напряжения в стержне, равные пределу текучести а7-е