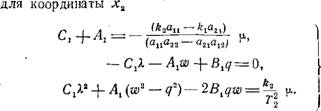ВЕТРОЭЛЕКТРИЧЕСКИЕ СТАНЦИИ

Внезапное изменение момента нагрузки при постоянной скорости ветра

Предположим, что во время работы ветродвигателя при постоянной скорости ветра момент нагрузки вне­запно изменился и в течение всего периода переходного процесса сохранялся постоянным. Тогда в соответствии с уравнением (2-21) § 2-4 частное решение по коорди­нате Х запишется в виде:

Х10 = — 7------ ^------- . f(t), (2-38)

Где f(t) — зависимость функции времени, характеризу­ющая изменение момента нагрузки.

Для этого случая в качестве начальных условий мо­гут быть приняты: л:1(0) = 0, х,(0) = 0, /7Ла(0) = 0 или л:!(0) = 0, л:2(0)'=0,/72л-а(0) = 0. Такие начальные усло­вия равнозначны и не противоречат исходной системе уравнений.

Так как процесс движения рассматриваем при v — = cons(, т. е. рь = 0, исходная система уравнений (2-20) § 2-4 после подстановки в нее начальных условий ^(0) = 0, х2(0) = 0, /7Л2(0) = 0 дает:

ТіРХі (0) = —/(0. 7І/Лка(0) = 0,

Откуда

Рх^О^-Щ, (0) = 0. (2-39)

Как следует из (2-37), для определения произволь­ных постоянных необходимо иметь значения первой и второй производной как для частного, так и для общего решения.

Так как в данном случае внешнее возмущение рас­сматривается в виде мгновенного скачка момента нагрузки от одного постоянного значения к дру­гому, согласно выражению (2-38) все производные от хо 'будут равны нулю.

Чтобы найти значение второй производной от хх, про­дифференцируем пёрвое уравнение исходной системы (2-20):

TiP**i + ЛпРХі а1грх, = 0.

Подставляя в него принятые начальные условия и зна­чение первой производной из (2-39), получим:

7-^-^/(0 = 0,

Откуда

Р*Мfit)- ' і

После подстановки в (2-37) значений х1 (0), л-10 (0) и их производных получим следующую систему уравнений для определения произвольных постоянных:

C-f А = .----- ^------ Г fit);

— СЯ — Aw - j - Bq = — ;

11

Ti

Величины Я, w и q определяются по корням харак­теристического уравнения (2-26) § 2-4.

Определив таким образом произвольные постоянные, можно вычислить общий интеграл движения:

^ = Се~и +е~« (A cos qt + В sin qt) - ■ fl ^ г f (t)

11 22 "2112/

(2-40)

И построить график изменения хх в функции времени.

Для координаты х2 будем иметь соответственно:

= сге~и +e~wi (A, COS qt 4- Вг sin qt) +

(апаг, — a2lan)

Принимая те же начальные условия, получим следу­ющие уравнения для определения произвольных посто­янных Av Ct:

С. 4-л1== —,------------------ 7 F(t,

1 ' 1 (апа22~ а21а12)

-C1X+B1q-rA1w = 0; 4 А1 (w2 — q2) — 2B, qw = 0,

Где w и q имеют прежние значения.

Результат применения формул (2-40) и (2-41) по­казан на кривых рис. 2-21, которые на примере ветро­двигателя 1D-18 характеризуют движение системы пос­ле полного сброса нагрузки.

Внезапное изменение скорости ветра при постоянном моменте нагрузки

Скорость ветра внезапно изменяется на величину ц и далее во время переходного процесса остается посто­янной. При таком условии частное решение по коорди-

Натам х, и х2 будет иметь следующий вид:

(Mag —Mia)

С точки зрения физического понимания процесса ре­гулирования при наличии внешнего воздействия со сто­роны ветра начальные условия: (0) =0, х2ф)=0, рхг(0)=0 ближе к действительности. Поэтому будем принимать их как здесь, так и в дальнейшем.

Подставляя начальные условия в исходную систему (2-20) § 2-4, получим:

= /Ле,(0) =

' і

Напишем уравнения для определения произвольных постоянных, полагая всё производные от Хю и х20 рав­ными нулю:

Для координаты х,

С+л=

Общие интегралы движения соответственно по коор­динатам и хл будут:

•V

(2-42)

-f В, sin qt) 4- (*'"»-*'"»>

11 7/1 (0,^22 — a2la,2

Характер движения системы при внезапном увели-

1

Чении скорости ветра на величину р,= -^показан на кри­вых рис. 2-22 для того же режима работы ветродвига­теля, при котором исследовался сброс нагрузки. Вне­запное увеличение скорости ветра мгновенно вызывает

Соответствующее увеличение и движущего момента

Д мв

Ветродвигателя х3= При этом точка, характеризу­

Ющая режим работы ветродвигателя, перемещается по исходной характеристике движущего момента, соответ­ствующей углу фо, в направлении уменьшения числа моду­
лей, так как в первое мгновение обороты ветроколеса еще не успевают измениться. Таким образом, степень увеличения движущего момента при таком внешнем возмущении будет в основном определяться аэродина­мическими свойствами самого ветродвигателя (его аэро­динамическими характеристиками) и кратностью поры­ва ветра.

Возможность появления на валу ветроколеса избы­точного момента необходимо учитывать при определе­нии запаса прочности отдельных элементов конструкции ветродвигателя и при исследованиях, связанных с обес­печением устойчивости работы генератора, когда ветро­электрическая станция предназначается для параллель­ной работы с другими неветровыми электростанциями. В рассмотренном выше случае увеличение движущего момента не связано со снижением запаса прочности пе­редачи, так как при заданных условиях (Жн = const) из­быточный момент полностью будет расходоваться на ускорение системы. Однако при наличии в схеме пере­дачи .мощности от ветродвигателя к генератору махо­вика (инерционного аккумулятора) увеличение движу­щего момента будет связано с соответствующими пере­грузками передачи, а следовательно, и со снижением запаса прочности.

Возмущение рассматриваемой здесь системы в виде мгновенного увеличения скорости ветра при постоян­ном моменте нагрузки является до некоторой степени условным, так как в природных условиях нарастание скорости ветра при порывах происходит с ускорением, имеющим конечные значения, а время действия порыва часто меньше времени переходного процесса системы от данного возмущения. Поэтому результаты вычислений, характеризующие изменение регулируемой величины, в данном случае должны получаться несколько завы­шенными.