ВЕТРОЭЛЕКТРИЧЕСКИЕ СТАНЦИИ

Расчет аэродинамических характеристик і ветродвигателя >и моментов, действующих на лопасти ветроколеса

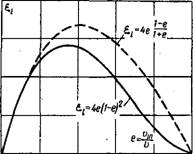
Аэродинамической характеристикой ветродвигателя называют зависимость отвлеченного момента ветроколе­са Мв и коэффициента использования энергии ветра

От числа модулей Z. Число модулей характеризует бы­строходность ветродвигателя. Определяется оно отноше­нием окружной скорости вращения ветроколеса радиу­сом R к скорости ветра, т. е Коэффициент

Использования энергии ветра мойсет быть найден из аэродинамической характеристики моментов:

1 = -^--^.2-а. г. (1-37,

NR2 р ~2~ *R3 р ~2~

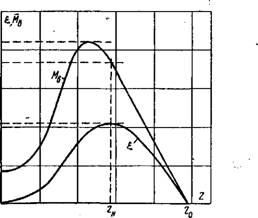
При расчетах и исследованиях работы ветродвигате­ля с электрогенераторами, приходится иметь дело со сле­дующими величинами, определяемыми по аэродинамиче­ской характеристике (рис. 1-10) и характеризующими его аэродинамические свойства.

__ 1. Начальный момент иди момент трогания с места Мтр определяется точкой пересечения характеристики моментов с осью ординат

2. Максимальный момент, который может развить ветродвигатель, Лімакс. _

3. Нормальный (номинальный) момент Мн, развивае­мый ветродвигателем при нормальном числе модулей ZH.

4. Нормальное число модулей ZH. Это число моду­лей, при котором коэффициент использования энергии ветра имеет максимальное значение £ = £ с.

5. Номинальная. скорость вращения ветродвигателя % определяется из выражения Zh = ; где vu — ско-

"н

Рость ветра, соответствующая началу регулирования.

6. Синхронное число модулей Z0 определяется точ­кой пересечения характеристики моментов с осью абс­
цисс. По номинальным значениям ZH, шн, ии, Ми ве­тродвигатель рассчитывается на длительный режим ра­боты.

Рассмотрим один из наиболее распространенных спо­собов расчета аэродинамических характеристик быстро­ходных ветродвигателей, основанный на теории Г. X. Са­бинина [Л. 2].

Разрежем площадь, ометаемую ветроколесом, цилин­дрическими поверхностями, концентрическими с осью ветроколеса, на ряд кольцевых струй, которые вырежут из лопастей элементарные отрезки. Таким образом-, ло­пасть представится разрезанной на отдельные элементы длиной dr. На каждый такой элемент, находящийся на расстоянии г от оси ветроколеса, действуют аэродинами­ческие силы dQ и dPa (рис. 1-7), которые создают мо­менты, стремящиеся повернуть его относительно двух осей: оси ветроколеса и продольной оси лопасти.

Аэродинамические характеристики вычисляют для каждого элемента лопасти отдельно, используя для этого следующие соотношения [JT. 2]: первое

Е і

Ibc^ = 8%r -77-:—ту;----------- г;-------------- j— , (1-38)

У (1 + е)(1 — ef (ctgp + (i)V 1 + ctg»p' V '

Позволяющее по выбранным геометрическим параметрам лопасти и заданным углам ее установки найти коэффи­циент торможения потока е на данном радиусе г в зави­симости от угла атаки а, второе

Ш Dr., (1-39)

В 1 + е Ctgg + n *'

Определяющее характер изменения отвлеченного момента по радиусу; третье

Служащее для определения числа модулей Z по найден­ным значениям е и р-

Расчет производится обычно ^в следующем порядке. Задаются различными значениями угла а. Так как

Р = <р —f - a, a <р — угол установки лопасти задан кон­струкцией ветроколеса, то из соотношений (1-38)—(1-40) последовательно определяют е, dMB и Z. Чтобы полу­чить полную характеристику, следует вести расчет для таких углов а, при которых коэффициент подъемной силы с изменяется от нуля до максимума.

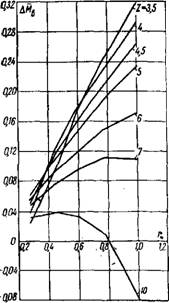
По данным расчета сначала строят кривые, харак­теризующие изменение элементарного отвлеченного мо - Щ

Рис. 1-11. Характер изменения Рис. 1-12. Характер изменения ДЛЇ в зависимости от Z. в зависимости от г.

Ментач ДМв на каждом радиусе в функции числа моду­лей (рис. 1-11). Затем для определенных значений Z строится диаграмма распределения ДМв вдоль лопасти (рис. 1-12). Наконец, путем графического интегрирова­ния кривых ДMB = f(r) находят значения отвлеченных
моментов Мв для всей лопасти при различных числах модулей, по которым строится аэродинамическая харак­теристика ветродвигателя.

Следует отметить, что подсчитанные таким образом значения Мв будут несколько завышенными, так как форму'лы, по которым производится расчет, не учиты­вают концевые потери, возникающие вследствие образо­вания вихрей, сходящих с конца лопастей. Концевые по­тери определяются по формуле [JI. 2]

8k

Где k — коэффициент, обычно принимаемый равным еди­нице.

При подсчете концевых потерь значение коэффициен­та торможения е необходимо брать средним из его зна­

Чении на радиусах конеч­ного элемента лопасти. Формулой (1-41) можно пользоваться при Z > 2 (это вытекает из самого вывода формулы). На рис. 1-13 приведена рас­четная аэродинамическая характеристика ветродви­гателя 1D-18 с учетом и без учета концевых по­терь. Как видим, концевые потери играют существен­ную роль. Их максималь­ная величина в ряде слу­чаев доходит до 15—20% от максимального момен­та. Кроме концевьих по­терь, имеются профиль­ные іпотерм, потери на

Кручение уходящей струи и потери, происходящие вслед­ствие неполного' использования всей ометаемой площади ветроколеса. Однако при определении аэродинамических характеристик ветродвигателей средней быстроходности (Z = 3—5) в первом приближении их можно не учитывать, так как они все вместе взятые по абсолютной величине Значительно меньше концевых потерь.

Аналогичным образом могут быть вычислены харак­теристики аэродинамических моментов, поворачивающих лопасти относительно их продольных осей. Необходи­мость в таких характеристиках появляется тогда, когда регулирование ветродвигателя осуществляется за счет поворота лопастей или их концов. Они нужны для рас­чета регулятора и исследования работы ветродвигате­ля в динамическом режиме. В этом случае как аэроди­намические, характеристики, так и характеристики пово­рачивающих моментов на лопастях приходится рассчи­тывать для разных углов установки лопастей ср.

Расчетные углы ср обычно выбирают так, чтобы мож­но было исследовать работу ветродвигателя на режимах Z, соответствующих заданному диапазону изменения ра­бочих скоростей ветра. Как показывает опыт расчета, для этого оказывается достаточно рассчитать характе­ристики для трех углов ер 'при v = vH, f = f с и v =

= "H+3MaKC (например, 8, 12, 20 м/сек).

Как известно, выражение аэродинамического момен­та, стремящегося повернуть элемент лопасти относи­тельно ее продольной оси, имеет вид:

И)?

DMa = mz0?-~-b2dr, (1-42)

Где т — коэффициент аэродинамического момента про­филя относительно точки О (рис. 1-7), равный

С

Mz~mz — (xe cos a -f у0 sin ct.)-f —

~(х0 sin а— у0 cos а) .

В экспериментальной аэродинамике коэффициент аэродинамического момента профиля т задается отно­
сительно передней кромки профиля как функция коэф­фициента с, т. е. mz = f(cy)._ Так как относительная скорость набегания потока на элемент лопасти равна:

= Vt + К+ uxJ= v (1 —Ђ)V 1 +Ctg2j3, выражение (1-42) можно записать в следующем виде: dMa = m^-f(l~-eV(l+ctg^) ЬЧг.

Ще

Q14

Чтобы получить отвлеченное значение этого мо­мента, разделим обе части этого выражения на рR3-^-:

DK = m?0bl (1 - е? (1 + ctg2 Р) dr., (і.43)

И b г

Где и. г#=——относительные значения хорды

И текущего радиуса. 40

Выражение (1-43) позволяет вычислить и построить такие же характеристики Ma~f(Z), как это было сде­лано для вращающего момента ветродвигателя Мв. Если

Выбрать одни и те же сечения лопасти и принять при вычислениях общие значения углов атаки, то оба расчета могут быть объединены.

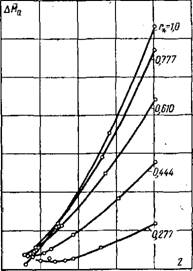
Характер изменения элементарных моментов АМа в зависимости от'г^ и Z показан на рис. 1-14 и 1-15.

Q1B

Q14

*

0,12 ЦЮ 0,08 0,06 0,0k

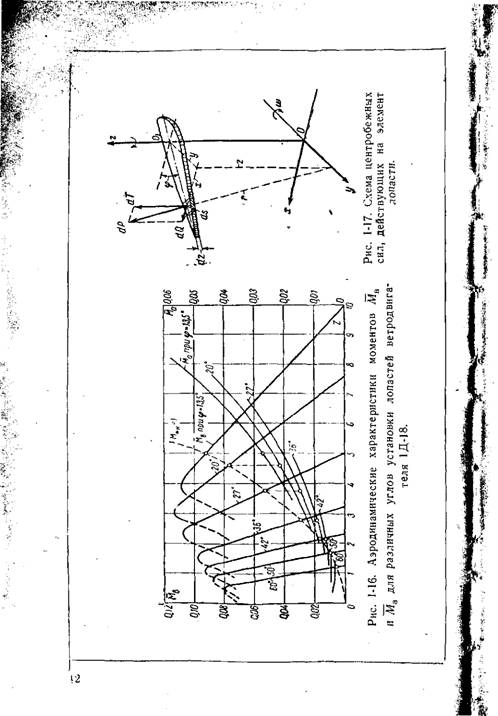
На рис. 1-16 даны аэродинамические характеристики и характеристики моментов, поворачивающих лопасти относительно их продольных осей, для различных углов установки лопастей ветродвигателя 1D-18. Абсолютные значения аэродинамических моментов, действующих на ветроколесо Мв и лопасти Жа, могут быть подсчитаны

Для каждого режима работы ветродвигателя по форму­лам:

Помимо аэродинамического момента на поворот­ные части лопастей при вращении ветроколеса действу­ют еще центробежные силы. Для определения величины момента от центробежных сил, поворачивающих лопасть относительно ее продольной оси, рассмотрим силы, дей­ствующие на элементарное сечение вращающейся лопа­сти, расположенное под углом' <р к плоскости вращения ветроколеса (рис. 1-17). Оси координат расположим так, чтобы ось oz совпала с продольной осыо лопасти, ось оу — с осью вала ветроколеса, а ось ох была перпен­дикулярна плоскости yoz.

Центробежная сила элемента сечения площадью ds будет равна:

DP = dz ds po)2r,

Где г— ^х2 - f - z2 — расстояние элемента от оси враще­ния.

Разлагая силу dP на две составляющие, параллель­ные осям ох и oz, заметим, что сила dQ стремится по­вернуть сечение лопасти относительно оси oz, а сила dT — переместить его вдоль оси oz. Из геометрических соотношений нетрудно убедиться, что сила

DQ = dz ds ршЪг

Остается неизменной при перемещении сечения лопасти вдоль оси OZ.

Величина момента от центробежных сил элементар­ного сечения лопасти, приходящаяся на длину dz, равна:

ЙМц — JJ югр ds х у dz = dz,

Где / —центробежный момент инерции поперечного сечения лопасти на радиусе r = z.

Полный момент, поворачивающий лопасть относи­тельно оси oz, при данном расположении ее в приня­той системе координат (т. е. при данном угле <р) буде т

У—■£>

= ^ = П-45)

Г=г„

Интеграл этого выражения представляет собой цен­тробежный момент инерции всей лопасти / относи­тельно оси oz. Отсюда следует, что для определения зависимости Л/ц = /(<р) должны быть найдены центро­бежные моменты инерции лопасти для различных углов ее установки.

Так как лопасти ветроколес, как правило, делаются полыми с каркасом нервюр и стрингеров и тонкой ме­таллической или полотняной обшивкой, определение цен­тробежного момента инерции лопасти сводится к нахож­дению суммы элементарных центробежных моментов инерции ее отдельных сечений. Для этой цели лопасть разбивают на ряд сечений, нормальных к оси oz, и сов­мещают их с плоскостью хоу. При наличии крутки все сечения должны быть расположены под соответствую­щими углами друг к другу, причем корневое сечение же­лательно расположить так, чтобы его геометрическая •хорда соівпадала с направлением оси ох.

По каждому сечению находят элементарные суммы:

2Д тх2, ЕД ту2, ЕД тху.

Далее путем суммирования сначала по отдельным сечениям, а затем по длине лопасти определяют момент инерции всей лопасти.

По элементарным моментам инерции относительно принятых осей координат можно определить элементар­ные моменты инерции относительно новой системы ко­ординат (х, у і) с тем же началом, но повернутой отно­сительно оси oz на положительный угол ф, используя для этого следующие формулы перехода:

X, = xcoscp4-ysin <р;

У г = у cos ер - f л: sin <р;

ІХі = L со§2 V + І у sin2 9 - !ху sin 2ср;

'у, К cos2 V + І у sifl2 ? + by sin 2cf'

І*,У, = 2?+ (/,-/,) sin^.

При тонких и нбкрученЫх лопастях или лопастях, имеющих сравнительно небольшую крутку, для опреде­ления момента Мц можно пользоваться формулой

И л 2

Где ср0 — угол между геометрической хордой сечения лопасти на радиусе г = 0,7/? и осью, относи­тельно которой центробежный момент инерции равен нулю; /л — осевой момент инерции лопасти; to — скорость вращения ветроколеса.