ВЕТРОЭЛЕКТРИЧЕСКИЕ СТАНЦИИ

ОСНОВЫ АЭРОДИНАМИКИ ВЕТРОКОЛЕСА

Из трех классов ветродвигател'ей—крыльчатые, кару­сельные и барабанные — для ветроэлектрических стан­ций, как правило, используются крыльчатые, как наибо­лее эффективные и обладающие наибольшей быстро­ходностью.

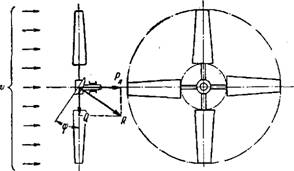
На рис. 1-6 показаіна схема крыльчатого ветроколе - са быстроходного типа, состоящего из четырех крыльев,

Закрепленных на общей втулке. Втулка с крыльями уста­навливается на горизонтальном валу, свободно вращаю­щемся в подшипниках. Крыло состоит из маха и закреп­ленной на нем лопасти. Лопасть образует с плоскостью вращения некоторый угол <р, который называется углом установки лопасти.

При воздействии на ветроколесо воздушного потока на лопастях возникают аэродинамические силы, приво­дящие ветроколесо во вращение. На каждый элемент лопасти воздушный моток набегает с. относительной ско­ростью Wi под углом а, называемым углом атаки.

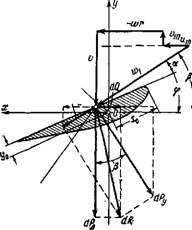
Рассмотрим скоростной и силовой треугольники эле­мента лопасти, взятого на радиусе г (рис. 1-7).

Пусть ширина элемента равна Ь, а длина dr. Тогда площадь этого элемента будет:

Ds — b dr.

Проектируя аэродинамическую силу dR на оси х и у, получим соответственно элементарное окружное усилие dQ и элементарную силу лобового давления dPл.

В экспериментальной аэродинамике принято аэроди­намические силы, действующие на элемент крыла, выра­жать через профильное сопротивление dPх и подъемную силу dPy. Как показано на рис. 1-7, эти силы можно получить, если спроектировать аэродинамическую силу dRa соответственно на направление относительной скорости и на нормаль к этой скорости. Тогда

ЙРл = dPy cos р + dPx sin £ dQ = dP sin p — dP cos I

Значения dP и dPx определяются По формулам:

DPу - J - ds;

U/i •

DPx = cxp -j - ds,

Где с и cx — коэффициенты подъемной силы и профиль­ного сопротивления; р — массовая плотность воздуха.

Коэффициенты с и с^ характеризуют аэродинамиче­ское свойство данного крыла. Их значения получают экспе­риментальным путем при продувках моделей крыла в аэродинамических трубах. Задаются они для каждого профиля крыла в виде зависимости cy = f(a) и cx = f(a).

Подставляя (1-12), (1-14) в выражения (1-13) и вводя

С

Величину обратного качества крыла р = —, после неко-

Су

Торых преобразований получим:

2 ї

Щ

АРл — сур Ь (C0SN~ $)dr> і

И)?

DQ = е^р —2~ b (sin p — jj. cos P) dr.

)

Чтобы определить значения dPл и dQ на каждом элементе крыла, необходимо знать его ширину Ь, вели­чину и направление относительной скорости wx и угол а, позволяющий определить величину коэффициента су. Однако, как это видно из треугольника скоростей (рис. 1-7), для нахождения величины и направления век­тора скорости w1 необходимо знать, кроме величины скорости ветра v и окружной скорости тг, еще величины скоростей о1п и и1п, называемых индуктивными. Скорости о1п и «,п возникают в результате воздействия вращаю­щихся лопастей на поток. ПоэТйму нельзя решить за­дачу расчета ветроколеса, не зная характера деформации потока, обтекающего ветроколесо.

Впервые связь сил, действующих на ветроколесо, с конструктивными параметрами лопастей и индуктив­ными скоростями, возникающими в потоке, была уста­новлена проф. Г. X. Сабинииум. Созданная им импульс­ная теория ветряных двигателей широко применяется до 'настоящего времени.

Рассмотрим основные положения этой теории.

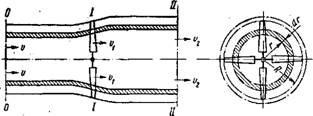
Представим себе, что равномерный поток воздуха под­ходит к ветроколесу со. скоростью v (рис. 1-8). Вращаю­щееся ветроколесо создает подпор, вследствие чего ско­рость потока по мере приближения к ветроколесу и не­которое время за ветрэколесом падает. Таким образом

В сечении 1-І скорость будет v1 = v~vln, а в сечении II-II— v2 = v — v2n (здесь vln и v2n—индуктивные ско­рости в сечениях 1-І и //-//). Давление воздуха в струе по мере приближения к ветроколесу повышается, но при прохождении через ветроколесо резко падает. За ветро - колесом образуется некоторое разрежение, которое в дальнейшем постепенно исчезает.

Вырежем из струи, обтекающей ветроколесо (рис. 1-8), на радиусе г элементарную кольцевую струй­ку толщиной dr. Воздух, заключенный в эту кольцевую струйку, действует на лопасти ветроколеса, вызывая си­лу лобового давления dPn и окружное усилие dQ. Вме­сте с тем по закону противодействия элементы лопастей, расположенные в кольцевой струйке, с такими же сила­ми будут воздействовать на воздушный поток, в резуль­тате чего в нем возникнут осевые Vla и окружные и1п индуктивные скорости.

Напишем выражение для импульса осевой силы. Им­пульс силы равен приросту количества движения воз­духа, проходящего через кольцевую струйку. Для интер­вала времени в 1 сек будем иметь:

DPJi~vdm — vadm—(v — v2)dm, (1-16)

Где

Dm = 2яг dr = const (1-17)

Есть масса воздуха, проходящая через кольцевое сече­ние в 1 сек, т. е. массовый расход струи, который в силу неразрывности потока будет одинаковым во всех сечениях.

Так как скорость в сечении //-// равна va — v — и2п, то выражение (1-16) можно записать в следующем виде:

DP=dmv2a. (1-18)

Окружное усилие dQ можно определить, применяя теорему о моменте импульса силы. До подхода к вет­роколесу струя не вращается, поэтому секундный при­рост момента количества движения будет равен dm X X и',п > где ип — скорость вращения струи непосред­ственно за плоскостью вращения ветроколеса. - Для интервала времени 1 сек получим:

DQr = dm-tin-r, (1-19)

Или

DQ — dm-u.

"In'

С достаточной точностью можно считать, что — — и2п, где и2п — скорость вращения струи в сечении II далеко за ветроколесом. Таким образом, выражение (1-19) можно записать так:

DQ= dm - и2п. (1-20)

Подставляя (1-17) в выражения (1-18) и (1-20), найдем:

DPJl = 2^v1v2ardr, | - dQ = 2«fv1u3ardr. f

Итак мы получили два вида форму^ для осевой и окружной силы (1-15) и (1-21): первый, — исходя из про­
филя лопасти, беря в основу формулы эксперименталь­ной аэродинамики, второй, — исходя из струи по секунд­ному количеству движения и по моменту количества движения. Приравняв полученные выражения, будем иметь:

Ш t

ЙРл — cy? i b (cos p - f jj. sin p) dr = = 2rcpv^j - dr,

DQ = сі ~y b (sin p — [A cos p) dr =

= 2npv1u2nr dr,

Где і — число лопастей.

Эти формулы импульсной теории проф. Г. X. Саби­нина являются основой всех конструктивных теорий расчета ветроколес. Разница между существующими. конструктивными теориями, позволяющими рассчитать и спроектировать ветроколесо, заключается в тех допу­щениях, которые делаются при подсчете индуктивных скоростей Vin, v2n и и1п, и2п.

В соответствии є вихревой теорией Н. Е. Жуков­ского

V2n ~ 2vln и й2п = 2й1п. (1-23)

По теории Г. X. Сабинина, учитывающей наличие при­соединенных масс в струе за ветроколесом, соотноше­ние индуктивных скоростей vln и v2a получается не­сколько иным, а именно:

2й1п

И2п=--------- (1-24)

1 + — 1 V

Полная осевая сила и окружное усилие всего ветро - колеса могут быть найдены по формулам:

U г„

Где г0 —радиус нерабочей части ветроколеса, не уча­ствующей в создании этих сил; R — радиус ветроколеса.

Момент относительно оси ветроколеса аэродинами­ческих сил, действующих на элемент лопасти, равен:

■ dMB = dQr.

Полный момент всего ветроколеса получим, проинте­грировав выражение

Го

Силы Ял, Q и момент Мв обычно выражаются в от­влеченных безразмерных величинах, причем силы отно-

V2 V2

Сят к —, а момент к тс/?3р - j - и вводят обозначение

Называемое относительным радиусом. Таким

Образом, отвлеченное выражение сил и момента запи­шем в следующем виде:

ItR2? ~Y 2P - g - "Я* ?~2

Практически интегрирование выражений (1-25) и (1-26) осуществляется графически, путем построения

Диаграмм ^л = /(0> 5Г = = W - Нахождение

Яг « ■ аг

* # #

Этих зависимостей производится на основе решений двух уравнений связи.

Выразим равенства (1-22) через параметры потока, соответствующие плоскости вращения ветроколеса. Если принять соотношение индуктивных скоростей по теории Н. Е. Жуковского (1-23), то равенства (1-22) примут вид:

Wj sw (1-28)

' І

Возводя в квадрат и сложив оба эти уравнения,

После некоторых тригонометрических преобразований получим:

"" (1 (1-29)

Wf 8-Г

По условию откуда

I+^^l+tgp»------- ^

Где — угол между dPy и (IR (рис. 1-7)

Подставляя (1-30) в (1-29) и извлекая квадратньпч корень из обеих частей равенства, получим:

V. W

1 1п =kibcy, (1-31)

Где ш1п = /rv2ln-- ип—относительная индуктивная ско­рость;

K — —----------------- коэффициент.

Onr COS [J.0

Это соотношение называется первым уравнением связи. Оно связывает скорости в струе (левая часть) с харак­теристиками профиля и формой лопасти (правая часть).

Если выражения (1-28) поделить одно на другое и заменить sin р и cos {3 их значением из треугольника ско­ростей (рис. 1-7)

Г Ml. > mi

То будем иметь:

"in (о. —Р""" —01и) = »1пК + І»01 + Иіи)- . (I-32)

Это выражение связывает окружную индуктивную скорость и1п с осевой индуктивной скоростью и1п и назы­вается вторым уравнением связи. С помощью этих двух уравнений связи и решаются аэродинамические задачи, связанные с расчетом и проектированием крыльчатых быстроходных ветродвигателей.

При проектировании ветроколеса обычно задаются законом изменения осевой индуктивной скорости v 1п по радиусу г в плоскости вращения ветроколеса. По зави­симости р1п =/(/•) и второму уравнению связи (1-32) определяют характер изменения окружной индуктивной скорости м1п =/(г). Знание индуктивных скоростей vln и и1п дает возможность определить треугольники ско­ростей и сил (рис. 1-7), действующих на отдельные эле­менты лопасти. Далее, на основании первого уравнения связи (1-31) для каждого элемента лопасти подсчиты­вают необходимые значения произведения ibc, позво­ляющие для выбранного профиля определить форму ло­пасти, т. е. <р(г) и b(r).

Имеется целый ряд практических методов расчета быстроходных ветродвигателей, подробное изложение ко­торых можно иайти в работах [JT. 1—3].

Теперь выясним, какую долю энергии воздушного по­тока, проходящего через ометаемую поверхность ветро­колеса, можно будет практически использовать с по­мощью ветродвигателя.

Согласно (1-1) и рис. 1-8 кинетическая энергия воздушного потока перед ветроколесом равна At —

Та* „ , т(в — v2nf =—g-» а за ветроколесом А2 = g • Но закону не­разрывности потока секундная масса воздуха в каждом сечении является величиной постоянной и равной:

M — ?Fv = ?F1v1 = ?Fava, (1-33)

Где F, Fa — площадь поперечного сечения струи, со­ответственно в сечениях 0-0, 1-І и //-//.

Если положить, что потери на ветроколесе отсут­ствуют, то энергия, снимаемая ветроколесом, будет:

Л^Л-Л^^-^^^т^ {v-Щ (1-34) Пусть

И2п=2и1п.

Тогда,, подставляя (1-33) в (1-34), получим:

А = ?Р^2п (v-^-pFAv-v^v^ .

Умножим и разделим правую часть этого выражений На 2У3:

Взяв отношение энергии, снимаемой ветроколесом, к полной энергии ветра, в сечении 1-І, получим идеаль­ный коэффициент использования энергии ветра:

РРгУ3 Л _ "in у Чп

2 v J v

Р F^3 Fiu3

= - е) (1-35)

Где е = коэффициент торможения потока в пло­скости ветроколеса.

Выражение (1-35) показывает, что зависит от величины потери скорости воздушного потока при про­хождении его через ветроколесо. Оно получено нами при соотношении индуктивных скоростей, вытекающем из вихревой теории Н. Е. Жуковского (1-23). Если же со­отношение этих скоростей візять по теории Г. X. Сабини­на (1-24), то идеальный коэффициент использования энергии ветра примет вид:

На рис. 1-9 приведена диаграмма изменения £г в зависимости от коэффициента торможения потока е, рассчитанная по уравнениям (1-35) и (1-36). Как ви­дим, максимальное значение коэффициента использова­ния энергии ветра равно (?г )макс = 0,593—0,687. Это есть предел, к которому должен приближаться коэф­фициент использования энергии ветра реальных ветро­двигателей.

При выводе формул (1-35) и (1-36) не учитывались различного рода потери мощности, связанные с вращени­ем ветроколеса в воздушной среде. К ним относятся: по­тери за счет образования. вихрей, сходящих с концов ло-

3-2412 33

ЙЗстей; профильные потери, йызванныё трейиём струй за ветроколесом и равные живой силе уходящей струи; потери вследствие неполного использования площади, ометаемой ветроколесом.

Практически максимальное значение коэффициента использования энергии лежит тз пределах £макс — 0,45— 0,5.

0.8

QB

Q2