ВЕТРОЭЛЕКТРИЧЕСКИЕ СТАНЦИИ

ИССЛЕДОВАНИЕ КАЧЕСТВА ПРОЦЕССА РЕГУЛИРОВАНИЯ

Возможность применения той или иной схемы регу­лирования ветродвигателя не может оцениваться толь­ко на основе одного факта устойчивости. В ряде случаев требуется, чтобы процесс перехода от одного режима работы к другому заканчивался в определенное время, а отклонение регулируемой координаты не выходило за установленные границы. Следовательно, кроме устойчи­вости, система должна обладать еще определенными качественными показателями.

Учитывая, что энергия ветра подвержена непрерыв­ным пульсациям, особо важное значение приобретают такие качественные показатели, как точность регули­рования, быстродействие, колебательность процесса.

В § 2-4 было показано, что процесс прямого ре­гулирования быстроходных ветродвигателей описывает­ся двумя уравнениями (2-21). Поделив члены этих урав­нений на Т22, Ти получим:

(Р3 + «іР* + а2р +'а3) х, =

~(Tt P2 + Tkp + ai3)f(t)]; (p3 + alP* + a2p--a3)x2 =

[(Ttk2p -[- a tlk, - ktaj p + a2J (/)],

' 2' і

Где alt аэ, a3 — коэффициенты характеристического урав­нения данной системы [§ 2-4, уравнение (2-25)].

Вид общего решения уравнений (2-34) зависит от кор­ней характеристического уравнения и представляет со­бой наложение переходного процесса на установившийся. При вещественных корнях общее решение будет:

JC, = + *10 = СіЄ-м - f + + JC10,1

X*=x*+xu=c; +c; e-v+c; +*20, J (2"35)

Где x ус,— общие решения левой части

* * » /п о л

Уравнении (2-34); x^q> х20 — частные решения, завися­щие от характера внешнего возмущения;

Сі, Са, Сз и С^ , с2 С3' — произвольные постоянные;

Xt, Я2, Я3— корни характеристического уравнения.

Если в числе корней, кроме одного вещественного, имеются комплексные сопряженные корни, то общее ре­шение запишется в следующем виде:

Х1 = Се~Х( -j-e~a'e (A cos qt-j-B sin qt) - f - JC10, | x2 = C^'-f e~wt (A, cos qt - f Bt sin qt) + x,0. і

Уравнения (2-35) и (2-36) показывают, что харак­тер переходного процесса в значительной степени зави­сит от вида внешнего возмущения, так как он - Через значение произвольных постоянных может изменять вид собственного движения системы.

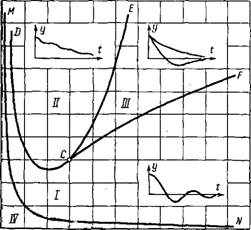
Учитывая, что-коэффициенты переменных в правых и левых частях уравнений (2-34) определяются через одни и те же параметры, приближенная оценка каче­ства процесса регулирования может быть сделана не­посредственно по коэффициентам характеристического уравнения. Если движение системы описывается урав­нением третьего порядка, как это имеет место при пря­мом регулировании ветродвигателей, то для таких иссле­дований удобно использовать расширенную диаграмму Вышнеградского [J1. 9], которая показана на рис. 2-20.

Чтобы воспользоваться этой диаграммой, необходи­мо характеристическое уравнение (2-26) § 2-4 привести к виду:

У* + Ау* + Ву+ 1=0,

Где _ _

Кривые СЕ, CF, CD и MN, построенные по уравне­ниям

Л2£2 _ 4 (А3 + В3) - j- 18 АВ — 27 = 0, 2А3~ 9АВ+ 27 = 0 (при А < 3), ЛВ= 1,

Разбивают диаграмму на четыре области[1]. В

1) области III соответствует апериодический зату­хающий процесс;

2) области II—монотонно затухающий процесс ко­лебательного характера;

3) области I — периодический затухающий процесс;

4) области IV—неустойчивый процесс.

Таким образом, на основании этой диаграммы, зная числовые значения коэффициентов характеристического уравнения, можно определить характер (переходного процесса во время регулирования. Для этого надо вы­числить коэффициенты Л и В и посмотреть, какой точке на диаграмме В ышнегр, адского они соответствуют.

Накопленный вычислительный и экспериментальный материал показывает, что при прямом регулировании быстроходных ветродвигателей поворотом лопастей или их концов обычно наблюдается колебательный харак­тер переходного процесса. Поэтому в дальнейшем для исследования движения таких систем при различных внешних возмущениях будем брать общее решение ви­да (2-36). Для определения произвольных постоянных С, А, В необходимо иметь три уравнения, которые по­лучим путем последовательного дифференцирования уравнения (2-36):

Xl = Ce~U - f e~wi (A cos qt - k В sin qt)-f x10 pxx — — CXe~v + e~wi [(Bq — Aw) cos qt — — (Bw - f Aq) sin qt] - f px10;

P*Xl — СЯ2<ГХЧ - e~wt {[A (w2 — q*) — 2Bqw] cos qt - f - f [В(ш2 — q*) + 2Aqw) sin qt) - f p*x10.

Для начального момента времени t = 0 эти уравне­ния имеют вид:.

Дг, (0) = С + А + дг1в (0); рхх (0) = - СХ - Aw - f Bq - f рх10 (0); р*хг (0) = СХ2 - j - А К — 92) — 2Bqw + Р*х10 (0).

Точно таким же образом можно написать систему уравнений для определения произвольных постоянных

^ь В і, С і.

Приняв начальные значения рассматриваемые пере­менных и задавшись характером внешнего возмущения р. и f(t), можно найти по уравнениям (2-37) произволь­ные постоянные, а затем и численное решение уравне­ний (2-36).

- Отметим, что при подобного рода вычислениях не­обходимо сверять задаваемые начальные условия с ис­ходной системой уравнений (2-20) § 2-4. Нужно пом­нить, что данная система допускает введение только трех произвольных начальных значений переменных (или их производных), а все остальные переменные (или их производные) будут от «их зависеть.

Рассмотрим характер протекания переходных про­цессов при регулировании в различных случаях.