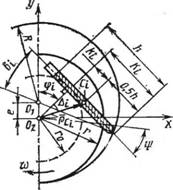
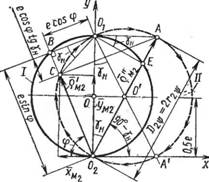
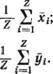УРАВНОВЕШИВАНИЕ НАСОСОВ
Насосы отличаются хорошей уравновешенностью. При работе насоса на фундамент не передаются значительные усилия. Неуравновешенность насосов при хорошей балансировке ротора может возникнуть только вследствие изменения положения центра масс вращающихся пластин. В общем случае при работе насосов возникают переменные по величине и направлению свободные силы вращения и возвратно-поступательного движения центра тяжести пластин. Эти силы пластин геометрически суммируются в общее силовое воздействие, вызывающее вибрацию фундаментной
|
|
Плиты и повышенное изнашивание подшипников. К транспортным насосам обычно предъявляют более жесткие требования по величине свободных неуравновешенных сил.
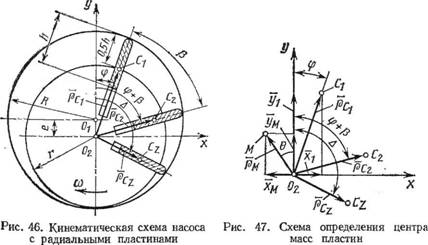
Рассмотрим общий метод нахождения мгновенного центра масс вращающихся радиальных пластин. Если центры тяжести пластин сосредоточены в точках С1? С2 ... Сг(рис. 46), то расстояние от оси вращения ротора 02 до центра тяжести пластин согласно формуле (2.12)
Pci = 02СХ = R (Ясовф + У- к2 sin2 ф - - А-) ;
РС2 = 02С2 = R [Яcos (Ф + р) + У - к2 sin2(Ф + Р) - - А.] ; Pcz = 02CZ = cosA+ |Л ->-2sin2A - - А),
2л
Где А = ф + (2-1)Р = ф + — (Z— 1), рад.
Векторы рсг могут быть разложены на горизонтальные xi и вертикальные yci составляющие (рис. 47):
Хг = R 8Шф ^ЯсОвф + У1 — А,281П2ф--- ;
Х2 = R sin (ф + Р) [ЯС08 (ф + Р) + к2 sin2 (ф - j - Р) - ■—] ;
Xz = R sin A (*,cos А + У1 - Я2 sin2 Д —.
Уг = R cos ф (Ясовф + ТА — к2 sin2 ф — -^-Л ;
^ 2 R J
У* = Rcos(ф + Р) [ясо8(ф + Р) + У -frsm»(q> + Р) - - А-] ;
Yz = /?cosA(^cosA + У- к2sin2 А--—-).
Координаты центра всех Z пластин (точка М, см. рис. 47):
|
|
|
*i + -------------- h xz Z |
|
Ул+У2----- H УZ Z |
|
Ум = |
(2.50)
|
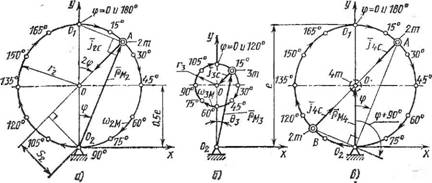
Рис. 48. Траектория движения центра масс пластин: А — 2 = 2; б — Z = 3; в — Z = 4; 0t — центр корпуса; 02 — центр ротора |
Радиус-вектор центра масс Z пластин
9м = ]/хм + ум. (2.51)
Угол отклонения радиуса-вектора рм от вертикали
6 = arctg (хм/ум). (2.52)
Рассмотрим влияние различных факторов на уравновешенность насосов.
Влияние числа пластин. Расчетная схема насосов с двумя радиальными пластинами при угле <р поворота дана на рис. 48, а. Из формул (2.50) ... (2.52) при H = 4е имеем:
ХМ2 = 0,5е sin 2<р; 1
А Г (2-53)
YM2 = ecosa<p; )
PM2 = ecos<p; (2.54)
62 = ф; 62 гаах = ±90°.
Система уравнений (2.53) представляет собой окружность в параметрическом виде с центром в начале координат.
Следовательно, центр масс одной пары диаметрально расположенных пластин перемещается по дуге окружности радиусом гг = 0,5е. Эта окружность расположена между центром ротора и центром корпуса (рис. 48, а). Масса двух пластин сосредоточена в точке А; со — угловая скорость центра масс пластин относительно точки О постоянна и в 2 раза больше угловой скорости ротора (рад/с):
<&2М — 2(0.
Таким образом, при повороте ротора на один оборот центр масс двух пластин дважды обойдет окружность с диаметром, равным е, причем при равномерном вращении ротора движение центра масс также будет равномерным. При таком движении на
Центр масс пластин действует постоянное центростремительное ускорение (м/с2)
J2C = 0,5есо 2м = 2есо2 = 2KRa2.
Ускорение центра масс пластин обусловлено силой, действующей в направлении ускорения. Несовпадение оси вращения ротора с главной центральной осью инерции подвижной системы ротор — пластины приводит к появлению нескомпенсированных свободных сил и моментов, вызывающих вибрацию насоса. Свободная сила (Н)
. ?2С = 2Mj2C = 4тЯ#со2, (2.55)
Где т — масса одной пластины, кг.
Свободную силу /*2С нельзя уравновесить или уменьшить с помощью «противовесов», закрепленных на вращающемся роторе, так как угловая скорость центра масс в 2 раза больше угловой скорости ротора. Момент от свободной силы относительно оси вращения ротора (Н-м)
М2 = F2CS2 = 2Т (XRaf sin 2q>, (2.56)
Где S2 — плечо свободной силы, м.
Максимальные значения момента М2 тах по модулю соответствуют углам поворота пластин ф = 45; 135; 225 и 315°.
При Z — 3 схема расположения центра масс пластин представлена на рис. 48, б. Аналогично предыдущему получим
_
Хмъ = -G- R Sin Зф, Ум» =-^- + -^#С05 3ф;
Рм» = + 16 - f 8Я cos Зф;
„ . % sin Зш
6а = arctg . 2.58)
4 + Xcos Зф v
Уравнения (2.57) представляют собой окружность радиусом г3, заданную в параметрическом виде, центр которой находится на расстоянии 0,5е от оси вращения ротора (рис. 48, б): r3 = VR/8.
Продифференцировав выражение (2.58) по углу ф поворота и приравняв его нулю, получим максимальные значения 83 тах, которые соответствуют углам
Ф1 =, ^90° + arcsin /3; ф2 = (270° - arcsin
6а шах = arctg 4
Ориентировочно можно принять <рг = 30° и ср2 = 90°. При Я, = 0,09 ... 0,18 угол 03 изменяется в пределах ±1,289 ... + 2,576°.
Следовательно:
Центр масс трех пластин перемещается по дуге окружности радиусом г3, причем г3 <• г2; центр О окружности находится на одинаковом расстоянии между центрами ротора и корпуса;
Угловая скорость центра масс постоянна и в 3 раза больше угловой скорости "ротора, т. е. созм = Зоз (рад/с);
Радиус-вектор рмз отклоняется от вертикали весьма незначительно.
Центростремительное ускорение (м/с8)
_ 2 9 -
/з с = Ггтм = -G- №R«>a.
Свободная сила (Н)
Fsc = Зт]вс = Цг - тЙЯсЛ (2.59)
■ь °
Момент от свободного усилия (Н-м)
М8 = ^ m№wa sin Зф. (2.60)
Из формул (2.55), (2.56), (2.59) и (2.60) видно, что свободная сила и максимальный момент в двухпластинчатом насосе значительно больше, чем в трехпластинчатом:
Fjo __ Щах _____ 32 л,*
"pgc ~~ мзтах ~ 27я *
Например, при Я = 0,18 отношение F2CFFsC = 5,58.
При Z 4 имеем
XMi = 0; yMi = 0,5е = const;
Рм4 = 0,5е = const; 64 = /4С = FiC = Мл = 0.
Следовательно, общий центр масс пластин не перемещается в плоскости вращения ротора, а расположен неподвижно посередине между центрами ротора и цилиндра. Расчетная схема уравновешивания насосов при Z = 4 может быть представлена двумя соосными двух пластинчатыми машинами, роторы которых повернуты один относительно другого на угол 90°. Центр масс одной пары пластин при угле ф находится в точке А (рис. 48, в), а другой пары — в точке В при угле 90° 4- 2ф. Общий же центр масс четырех пластин будет лежать в точке О при Любых положениях ротора. Таким образом, при Z = 4 насос будет полностью уравновешен. Аналогично предыдущему общий центр масс пластин при Z = 6, 8, 12, 16, 24, ... по тем же соображениям не будет менять своего положения при вращении ротора. Теоретически
|
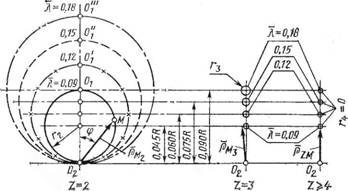
Рис. 49. Изменение траектории движения центра масс пластин в зависимости от относительного эксцентриситета для различных чисел пластин |
Было показано, что и для других чисел пластин Z > 4 положение центра масс пластин от угла поворота ротора не зависит, т. е. насос в этом случае полностью уравновешен.
Влияние эксцентриситета. С увеличением относительного эксцентриситета неуравновешенное усилие в насосе при Z = 2 возрастает в первой степени [см. формулу (2.55)], а при Z — 3 — Во второй [см. формулу (2.59)]. Однако во втором случае свободная сила во много раз меньше [см. формулу (2.61)]. На рис. 49 представлены траектории движения центров масс пластин при различных значениях К и числе пластин. При Z ^ 4 траектории центров масс вырождаются в точки.
Влияние массы пластины. Свободное неуравновешенное усилие в насосе при Z = 2 и 3 пропорционально массе пластины.
Влияние угловой скорости ротора. Для заданных конструктивных размеров вакуумного насоса неуравновешенное усилие прямо пропорционально квадрату угловой скорости. При неизменной теоретической быстроте действия с увеличением угловой скорости ротора размеры насоса уменьшаются. Геометрическая быстрота действия (м3/с)
F Sr = CReLn = С (-£-) RS(* = Откуда радиус цилиндра (м)
R = V Sr/(Cl(o).
Свободная сила при Z = 2 с учетом этой формулы (Н) ~F2C = 4MiRo* = 4 (4) ) =
Рис. 50. Кинематическая схема насоса с наклонными пластинами
|
|
Коэффициенты пропорциональности: 30
Р — плотность материала пластины, кг/м3.
Аналогичные результаты получают и при Z — 3. Таким образом, с изменением угловой скорости ротора свободное усилие пропорционально <м2 при неизменных размерах насоса и пропорционально со2'3 при постоянной теоретической быстроте действия.
Влияние угла наклона пластин. Кинематическая схема насоса с наклонными пластинами показана на рис. 50. За текущий угол поворота ротора принят угол <рг, образованный линией центров OjOa и радиусом, проведенным перпендикулярно к плоскости i-й пластины. Радиус-вектор центра масс t'-й пластины
Рсг = Го/cos Дг,
Где
|
Рис. 51. Траектория движения центра Масс двух наклонных пластин: Ох — центр корпуса; Ов — центр ротора
|
|
J^51 0Z Л£ |
|
Где Сх, С2 и С — С1 = |
|
(2.62) (2.63) (2.64) |
R0 = г sin "ф = R (1 — Я) sin я|;;
Ki .
Дг = arctg -
|
(2.65) |
|
Отсюда |
Ki ' Ki —Y > Kt — RcosSi —es'm cpi.
|
[(1 — A)sin|) — Ясовфг]2 |
Cos 6* = Следовательно,
Kt = R{Y 1 - [(1 - Я) sin ф Я cos ф;]2 — ЯвШфг}.
Для (i + 1)-й пластины аналогично
Kl+1 = R{Y~ 1 — 1(1 — Я) sin ф — Я cos Фг+х]2 —■ Явйфад}, где <Pi+i = <Pi +-g-, рад.
Подставляя значение Ki в формулу (2.65) с учетом выражений (2.63) и (2.64), из формулы (2.62) находим радиус-вектор рсг. Его проекции на координатные оси xt = рС1 sin (фг + А») и yt = = Рсг cos (фг + А,).
Для насосов с двумя наклонными пластинами координаты центра масс
Хмъ = — 0,5 (Ih-kz) cos ф, |
Ут = 0,5 (kt — kz) sin <р; J
Рм2 — Y~XM2 + y2M2 — ^R sin ф — Ар, (2.67)
Где Др = - у- {у^ 1— [(1— Я.) sin - ф — Ясовф]2 —
— V1 —[(1 — Я) sin - ф -f Я cos*|>] 2}«
При отрицательных значениях хМ2 величина Ар > 0, при положительных Ар < 0.
Выражение (2.67) определяет траекторию движения центра масс двух наклонных пластин в полярной системе координат в общем виде. Значение Ар определяют из прямоугольного треугольника ВСОх (рис. 51):
Ар = ВС = ea^tg-y,, = A/?cos9tgYH, где 7н = arctg ty 1 — Ш — sin — Я]2 —
— У1 — [(1 — Я) sin - ф + Я]2}/(2Я).
При угле наклона пластин яр = 20° и А = 0,18 угол y„ = = 16,59°. Для радиальных пластин = 0° и Ар = 0. Тогда Рмг — ^R sin ф. Эта формула тождественна выражению (2.54).
Траектория движения центра масс двух наклонных пластин построена на рис. 51 — линия II. Выражения (2.66) и (2.67) представляют собой окружность диаметром D^ = 2ггф:
D = рм = АОъ = KR/cos уи.
Центр окружности находится в точке О' с координатами Х0- = 0,5 KR tg Ун = 0,5 D sin У0. = 0,5Я#.
Для сравнения на рис. 51 траектория движения центра масс двух радиальных пластин обозначена линией I.
Следовательно:
1. Центр масс двух наклонных пластин перемещается по окружности, проходящей через центры ротора и корпуса и смещенной вправо от оси центров при вращении ротора по часовой стрелке; с увеличением угла наклона пластин диаметр окружности и ее смещение возрастают.
2. Угловая скорость центра масс пластины постоянна и, так же как и для радиальных пластин, в 2 раза больше угловой скорости вращения ротора, со2М = 2со.
3. Свободная сила у насосов с наклонными пластинами на 2 ... 5 % больше свободной силы в случае применения радиальных пластин:
F2C = 4mkR(d2/cosyH. (2.68)
Из выражений (2.55) и (2.68) следует, что
4. Траектории движения центров масс трех пластин представляют собой окружности радиусами гзф и с центрами в тех же точках, что и в случае двухпластинчатого вакуумного насоса (линии ///, рис. 52, а). При этом щм = Зсо.
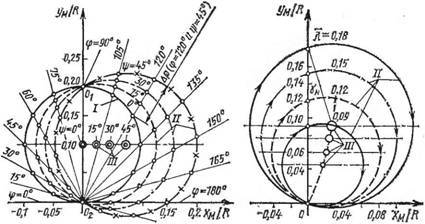
|
Рис. 52. Изменение траектории движения центра масс пластин: А — прн Л. = 0,2 для различных углов i]> наклона; 6 — при i]> = 20° для различных значений Я; / — радиальные пластины, Z — 2; // — наклонные пластины, Z = 2; III — Наклонные пластины, Z — 3 |
|
О) Ю |
5. При Z 4 для любых значений углов наклона пластин их общий центр масс не изменяет своего положения на плоскости при вращении ротора, т. е. в этом случае насос полностью уравновешен.
Изменение траекторий наклонных пластин при г|з = 20° для различных значений Я представлено на рис. 52, б. Центры окружностей при различных Z и Я лежат на общей кривой OA