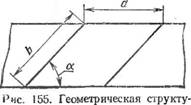
ТЕОРЕТИЧЕСКАЯ ХАРАКТЕРИСТИКА РАБОЧЕГО КОЛЕСА И ЕЕ ОСНОВНЫЕ ПАРАМЕТРЫ
Теоретическая откачная характеристика рабочего колеса турбомолекулярного вакуумного насоса определяется, как сказано, максимальной быстротой откачки Smax при отношении давлений, равном единице, и максимальным отношением ттах давлений при быстроте откачки, равной нулю. Характеристика колеса зависит от отношения окружной скорости и скорости теплового движения молекул, геометрии межлопаточного канала (угла а установки лопатки или наклона паза, отношения ширины межлопаточного канала к его длине), а также от закона взаимодействия молекул газа со стенками межлопаточного канала.
|
Ра межлопаточного канала |
Построение теоретической модели перехода молекул газа через межлопаточные каналы или пазы рабочего колеса должно быть таким, чтобы при ряде допущений, существенно не искажающих сущности происходящих при откачивании газа явлений, оказалось возможным получение зависимостей для максимальной результирующей вероятности и максимального отношения давлений в форме, удобной для их теоретического анализа с целью определения оптимальной геометрии межлопаточного канала на заданные условия работы [14].
|
|
Величины потоков молекул газа, проходящего через рабочее колесо, во многом зависят от закона взаимодействия молекул со стенками межлопаточного канала или паза. Взаимодействие разреженных газов с твердой поверхностью часто удовлетворительно описывается диффузным законом. В некоторых случаях, например при больших углах падения, закон отражения от шероховатой поверхности близок к зеркальному, причем тем больше, чем больше скорость молекул.
Для описания взаимодействия молекул с поверхностью часто используют модель, предложенную Максвеллом, которую строят в предположении, что часть молекул о отражается от поверхности диффузно, а остальные (1 — о) — зеркально.
При построении теоретических моделей принимают, как правило, следующие допущения: режим течения газа в рабочей полости молекулярный; распределение молекул по скоростям соответствует закону Максвелла; движение молекул в канале рабочего колеса (т. е. в плоскостях, перпендикулярных торцовым поверхностям колес) двухмерное; температура газа и внутренних поверхностей насоса не меняется в процессе откачивания; взаимодействие молекул газа со стенками межлопаточного канала или паза при переходе на противоположные стороны рабочего колеса описывается диффузным или зеркальным законами, или тем и другим одновременно.
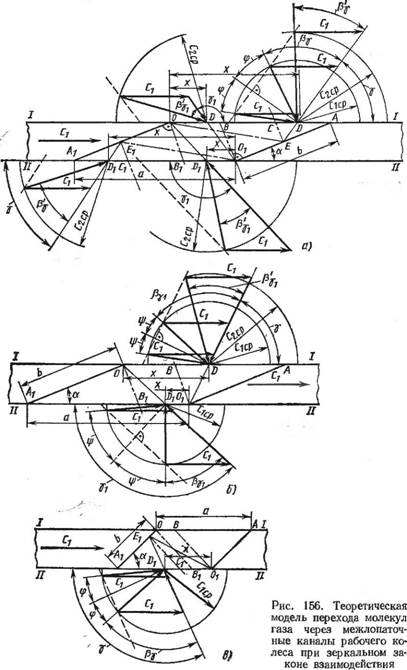
Основные параметры откачной характеристики насоса при зеркальном законе взаимодействия молекул газа со стенками межлопаточного канала можно получить, рассмотрев теоретические модели, представленные на рис. 156.
Пусть молекула, относительная тепловая скорость которой С = V/VH меньше относительной скорости движения межлопаточного канала сг = U/VH, попала в окрестность Dx точки D £ (ахх) (рис. 156, а). Молекула перейдет через межлопаточный канал, геометрические размеры которого удовлетворяют соотношению а b cos а, если вектор ее средней относительной скорости будет принадлежать области, ограниченной углом (я — 2ф). В этом случае с»
J cf (с) dc
CLcp — т, • J' f (с) dc О
Угол, при нахождении в плоскости которого вектора ср молекула после столкновения со стенкой канала О^А отражается от нее на сторону /-/, ф = я/2 _ pv>
Где Рт = Arcsin ( —— Sin?) ;
clcp '
Х — 2A sin2 А у — arcsin. .
V (2A sin a cos а)2 + (х — 2A sin2 а)2
Вероятность того, что молекула, средняя относительная скорость которой с1ср, попав на участок ахъ перейдет со стороны I—I на сторону II—II,
|
Xi |
Яи = р(0<с<с,)^М Ndx—J2 (Pdxj,
xt
-1
Где P (0 с Cj = | F (C) Dc Хг — значение X, при котором угол ф равен нулю 0
Или изменяется в зависимости от соотношения скоростей (сх и с1Ср) и геометрических параметров канала (а, Ь, а):
^ я а при A Sz ;
Я
А при A<—G-, Я
*1 =
Аг при А<—, с>Л1>В1;
Я
Вг при а < , А1 ^ Bj
{At — значение х, при котором Clcp= CI S*N V> т- е - ПРИ всех х ^ Угол Ф = 0; Ах = 2A Sin A [Sin а Cos A V(C1/C1 ср)2 — 1; Вг—значение*, при котором ОБ = = ОС, т. е. изменяется функциональная зависимость <р= / (а, Ь, а, сл, с1Ср), Вл — 2А (а Cos А — Ь)/(2а Cos а — 6).
|
Ь1Ср X + B Cos A — A |
Если ^ Вг и л; < то молекула, попавшая в окрестность Dx точки D £ (хгхг), со средней относительной скоростью сг ср перейдет со стороны I—I на сторону II—II, если вектор ее скорости будет лежать в плоскости угла (л—2ф), где ф — значение угла ф при х < Вг (рис. 156, б):
Ф = - у - — pvl; pvl = arcsin sin Yi) ; Vi = arcsin -
V (A — X)2 — 2b (a — x) cos a + B2 '
Вероятность того, что молекула, средняя относительная скорость которой равна сг ср, попавшая на участок хгх2, перейдет со стороны I—I на сторону II—II,
|
( |
Xi Xi
ndx— J 2tpdx,
Х2 Хг )
Где х2 — значение х, начиная с которого ф Ф 0:
|
X* = |
А2 при Ах < В1ш А2^Вх,
Вг при Ах<Вх, А2> Вх, а ^ ;
Хг при а < —
(А2 — значение х, при котором сх ср= сд Siny1, т. е. при всех х А2 угол = = О, А2 = а — B cos а -(- ^ s'n а V(Ci!C ср)2 — !•
Молекула со скоростью с1ср, попавшая на участок х20 входа в межлопаточный канал OA, перейдет со стороны /—/ на сторону II—II, если вектор ее скорости будет лежать в плоскости развернутого угла я; вероятность перехода этой молекулы
Если тепловая скорость молекулы V > и (с > С]), то молекула, попавшая в окрестность Dx точки D £ (ах3) (см. рис. 156, а), перейдет со стороны I—I на сторону II—II, если вектор ее относительной скорости с2 ср будет принадлежать плоскости угла
(у + Pi);
Со
J cf (с) dc
Саср = 5------------ J Pv = arcsin sin у) .
J f (с) dc
Ci
Вероятность перехода молекулы со средней относительной скоростью с20р, попавшей на участок ах3,
А
Ки = Р {сг <с < оо) -jL - J (у + Pv) dx>
X.
Где Xs = Вл—значение х, при котором углы у и pv меняют значения, т. е. О В = ОС.
Вероятность перехода молекулы со средней относительной скоростью с2 ср, попавшей на участок х30 входа в межлопаточный канал OA (рис. 156, б),
*ж
Кк = Р (сг < с < сю) -L- J (у, + р;,) Dx,
О
Где р'j = arcsin sin Vj ) .
С2Ср /
Таким образом, вероятность перехода молекул газа со стороны всасывания I—I на сторону нагнетания II—II
|
= р(0<с<сх) |
|
Я а |
|
-f р (сг < с < оо) 1 |
|
Па |
Кг зеР = Кгг + Кц + Ki3 + Ки + ^15 = 1
TOC o "1-3" h z A a Xt
J я dx — J 2ф dx — J 2г|)dx +
0 Xi x2 J
A x „ "j
X. D J
Аналогично определяется вероятность Кц аер перехода молекул со стороны нагнетания II—II на сторону всасывания I—I.
Пусть молекула, обладающая средней относительной скоростью сг ср, попала в окрестность Dx точки Юг £ (х4хб) входа в межлопаточный канал 01А1 со стороны II—II (рис. 156, е). Молекула перейдет на сторону I—I тогда, когда вектор ее скорости будет лежать в плоскости угла 2tp.
Вероятность того, что молекула, попавшая на участок х4хь Со средней относительной скоростью с10р, перейдет со стороны II—II на сторону I—I,
Л4
Kill = Р(0<с<сО —J<pdx,
Хъ
Где х4 — значение х, при котором для всех угол <р = 0:
А при А4^а; Хц= ■ Ац при а>А4>В1 . хъ при Ац Вг
(Ai — значение х, при котором С1СР = с1 Sin У, т. е. при всех х угол ф = 0, At = 2A Sin A [Sin А — Cos A LA(C1;/C1CJ))2 — 1]; хь — значение х, при котором угол ф меняет свою функциональную зависимость от соотношения скоростей и геометрических параметров межлопаточного канала:
' Вг при A4^s Вг; хъ= Аъ при А4 < Вц „ 0 при А4 <; 0
(Аь — значение х, при котором угол ф = 0, т. е. Clcp= Sin Vi. Аь = А — — B cosa — B sin a V(Cki cj>)2—1 (см. рнс. 156,6)].
Если молекула попадет на участок хьОг входа в межлопаточный канал ОгАг со средней скоростью с10р, то вероятность ее перехода на сторону I—I (см. рис. 156, б)
Х.
Km = р (0 <с <ct) J pdx
Молекулы с относительной скоростью с > сх, попавшие в окрестность Dx точки Бг £ (ах3) (см. рис. 156, а) входа в межлопаточный канал 01Л1, перейдут со стороны II—II на сторону /—I, Если векторы их скоростей с2ор будут принадлежать области, ограниченной углом у—а молекулы, попавшие на участок х30, Перейдут на сторону /—/, если векторы их скоростей будут лежать в плоскости угла Vi—Pvi-
|
Па |
В этом случае вероятность перехода со стороны II—II на сторону I—I
А х3
Кщ =p(ci<e<oo).
Таким образом, вероятность перехода молекул газа через межлопаточный канал со стороны II—II на сторону I—I
Ки зер = Кщ + Ки2 + Kus = р (0 < с < Сх) х
|
( |
Xt хъ
<i)dx + ^dx + р{с1<с<°о)-±- X
О /
А хг П
О J
Если геометрия межлопаточного канала удовлетворяет соотношению а < fc/cos а, то зависимость углов ф, у и от соотношения скоростей и геометрических параметров межлопаточного канала не изменяется. Однако в этом случае х2 = хи Вх = О,
XS — Xt)
= 0. Следовательно, для межлопаточных каналов, параметры которых удовлетворяют соотношению а < ЫCos а, вероятности Ki зер и Ки зер соответственно равны:
Ki Зер = р (0<с ^Jta — 2 J ф^ +
А
+ р (ci <с < оо) JL j (Y _j_ p;) dx-,
0
Xt
KIiЗер = P (0 <C < CX) — j ф Dx +
О
A
+ p (Ci < с < оо) J (y - p^,) dx.
0
Результирующая вероятность перехода молекул газа через рабочее колесо при зеркальном законе взаимодействия их со стенками межлопаточного канала или паза
Ктах зер = Ki зер "
-Ки зер>
А максимальное отношение давлений
Тщах зер = Ki вер/К и зер-
Рассмотрим возможность перехода молекул на противоположные стороны вращающегося рабочего колеса насоса при т = 1 с учетом диффузного закона взаимодействия молекул газа со стенками межлопаточного канала. При этом за направление отражения молекул газа будем принимать преимущественное, совпадающее с нормалью к поверхности стенок межлопаточного канала рабочего колеса. При такой модели отражения молекул от поверхности сохраняются средние характеристики отражения и значительно облегчаются аэродинамические расчеты в разреженном газе. Близость суммарных результатов для лучевого и диффузного отражений оправдывает метод усреднения функций отражений молекул газа от поверхности [3].
Определим вероятность перехода молекул со стороны /—/ на сторону II—II при следующей геометрии межлопаточного канала или паза (рис. 157, а): ЫCos а а B cos а.
Пусть молекула попала в окрестность точки С £ Ах0. Как следует из рис. 157, а, молекулы, обладающие тепловой скоростью
Ci
| Cf (с) Dc Clcp = Tt »
J f(c)dc
О
Перейдут со стороны I—/ на сторону II—II, если вектор их средней скорости будет лежать в плоскости угла 2ф—2я];. В этом случае вероятность перехода молекул со стороны I—I на сторону II—II
2
Хо
Где Хг = а; х0= а — 6 Cos а -F- 6 Sin а ^(Cj/Cj ср)2 —1 при 6 Cos а > 6Sin а х X LA(Cl/Cl ср)2 _J — значение х, при котором сг ср= Ct Sin У, т. е. угол я]) = 0.
При 6 Cos а < 6 Sin А |F {рх1сх ср)2 — I х0= хг, так как = 0 во всей области изменения л: от 0 до а;
Ф = — Рг; ^ = -?Г — Pv;
Pi = Arcsin ( Sin i ) ; Py = Arcsin (—sin У ) ;
cicp / cicp J
(B — A cos a) sin a
I - arcsin
+ 2Д:(b — a cos a) cos a + (b — A cos a)2' Bsina
У = arcsin
У (a — X)2 — 26 (a — X)cosa+ i
Если молекула попала в окрестность Dx точки С £ (х0х4) со скоростью с1ср, то молекула перейдет со стороны I—/ на сторону II—II при условии, что вектор ее средней скорости будет лежать в плоскости угла 2ф.
Рис. 157. Теоретическая модель перехода молекул газа через межлопаточные каналы рабочего колеса с учетом диффузного закона взаимодействия
В этом случае вероятность перехода молекул со стороны /—I на сторону II—II
2 Х°
= р (0 < с < сг) — [ф Dx,
Где х4 — значение х, при котором сг ср = сх Sin I,
|
{ |
А при 0 ^ А ^ х0; О при А 0; Х0 при А^хО
[а = (Ь - A sin a) (sin а]/ - 1 - cos а) ] .
Если молекула попадает в окрестность точки С £ OA со скоростью с > сх (рис. 157, б), среднее значение отношения которой к наиболее вероятной скорости
J cf {с)
Ct
С2 op —
I dc
То она пройдет со стороны /—/ на сторону II—II при условии, что вектор ее средней скорости будет лежать в плоскости угла
(Y + Pv - * - Р»)-
Вероятность перехода молекул со стороны I—I на сторону II—II
Хх
|
Где |
Ян = р {Сх < С < оо)-^- j (Y + Pv - I - pf) Dx,
P (c1^c<oo) = | f (c) dc; Хг = А-, Хг = А—6 cos a; x3 = 0; P; =
= arcsin f—^i—sin I); pT = arcsin ( —-— sin У J .
C2 OP ' C2 Op '
Угол y в зависимости от геометрических параметров межлопаточного канала может быть больше 90°. В этом случае вероятность перехода молекул
Г хг
Я13 = Р {Сх < с < «О-У f (Pv - * - Pi) dx +
Xy x%
+ ^ Y dx + J (n — Y) dx I.
Рассмотрим вероятность перехода молекул со стороны II—II на сторону /—I. Молекулы, обладающие скоростью с1ср, не перейдут со стороны II—II на сторону I—I, если Сх £ {АхО^) (см. рис. 157, а). Тогда вероятность перехода молекул со стороны II—II на сторону I—/
ХJ
Яш = Р (Ci < С < оо) -L- J (Y — рт - I + р,) Dx,
Где хх = а; х3 = 0, Или
Lxs
XI || + ydx+ J (я — Y) dx .
|
Dc |
|
J/w« |
Xz X*
Если молекула, обладающая скоростью 0 с < съ среднее значение отношения к VH которой сх ср попадает в окрестность точки С £ фХ0), то молекула не перейдет со стороны II—II На сторону /—I.
Молекула, попавшая в окрестность точки Сх £ (XD0L), перейдет со стороны II—II на сторону I—/, если вектор ее средней тепловой скорости будет лежать в плоскости угла 2ч]? (см. рис. 157, б).
В этом случае вероятность перехода молекул со стороны II—II на сторону /—I
Km = Р (0 < с < Су) ~ J Ip Dx,
Где х0 — значение х, при котором Ct Ср = сг Sin у; Х0 = а — Ft Cos а —Ft Sin а ср)2 — 1
При B cos а + Ft sin a r(cllc1 Cp)2 — 1 < A; X0 = X3 при B cos а -f- b sin a l/Vi/ci cp)2 — 1 > O.
Таким образом, значения общих вероятностей перехода молекул со стороны I—I на сторону II—II и обратно соответственно равны:
Kw = Кц + Кп + Л'та и KUn = Кш + Л'ш-
Рассмотрим геометрию межлопаточного канала или паза, когда а ^ B cos а. В этом случае
При этом
Хг = а; = х3 = 0; х0 = A — B Cos а +
+ H sin а jA(Сл/С! op) — 1 при B cos а > B sin a V(Cxjc]_ cp)2 — 1; X0 — xx при b cos a <z b sin a ~f (cjci cp)2 — 1.
Тогда
Kin = Kn + Kj$ + КI3 и Kim — Кщ-
Если геометрия межлопаточного канала или паза удовлетворяет соотношению ЫCos а ^ а, то t = рг = 0. Тогда
Ki1 = p(0<c<c1)-^-f(f-^)dx,
Xq______
Где Xt = а; х0 = а — B Cos а + B Sin а V(сг/сг ср)2 — 1 при Ft Cos а > Ft Sin A ^(CJ/CJ Cp)Z — 1; х0 = хх при 6 Cos а < 6 Sin а V(CI/CI ср)2 — 11
Ка = Р (сх < с < оо) J (Y + Pv) Dx.
*8
X, Xi
|
*= p (cx < с < oo) J^- |
Xi
Я//1 = р(0<с<оо)^ j (Y — Pv) Dx. При y>90°
X± Xi
J y dx-- ^ (it — Y) dx — j fly dx
L*i
*0
Я№ = p (0 < с < Cjl) — j Ф dx,
Где x2 — a — 6 cos а; x^ = 0;
X0 = a — 6 cos а — 6 sin a Vic^jcx cp)2 — 1
При A ^ b cos а + B sin а V(cilci Cp)2 — 11
X0 = X3 при A <c b cos а + B sin а V(Cxl^i cp)2 — 1*
Результирующая вероятность перехода молекул газа через межлопаточный канал или паз рабочего колеса с учетом диффузного закона взаимодействия их с поверхностью
ЯгаахЛГ = Я/JV - Кцц, а максимальное отношение давлений
ТтахЛГ = ЯТ!ЯUN •
Как показали теоретические исследования, переход молекул газа через межлопаточный канал с учетом диффузного или зеркального законов взаимодействия при двухмерном и трехмерном движениях зависит от площадей сечений межлопаточного канала на начальном и конечном радиусах. Из-за сравнительной их малости по отношению к площади боковых стенок или торцовой площади межлопаточного канала влияние площадей этих сечений на процесс перехода молекул газа пренебрежимо мало. Вследствие этого при определении основных параметров откачной характеристики рабочего колеса насоса процесс перехода молекул газа через межлопаточный канал правомерно рассматривать, принимая движение молекул двухмерным. При этом не изменяется сущность явления перехода молекул газа через межлопаточный канал и практически отсутствуют количественные различия, однако решение уравнений для определения основных параметров откачной характеристики значительно упрощается.
|
При v>90° Я/8 = Р (Ci < С < ОО) |
|
Я а |
|
J Pv dx + J У Dx + ^ (it — Y) Dx; |
Таким образом, процесс перехода молекул газа через межлопаточные каналы рабочего колеса может быть выражен теоретической моделью, в соответствии с которой их взаимодействие
Ftmax
|
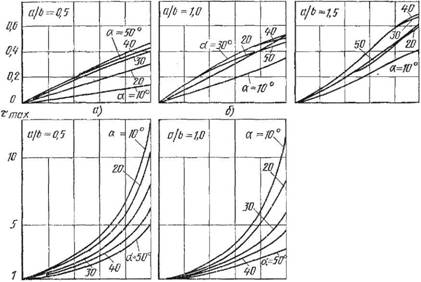
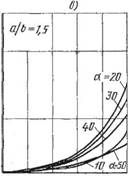
0,1 № 0,6 Цв'С, 0 0,Z Dfi 0,5 О, Б с1 О 0,Z 0,4- 0,6 О, В Cj Г) д) е) Рис. 158. Теоретические характеристики рабочего колеса насоса, определенные с учетом зеркального и диффузного законов взаимодействия молекул газа со стенками межлопаточного канала: |
А~в ~ Кгшк = F (и>«яУ- г~е ~ тшах = F ("/»н)
Со стенками канала или паза рассматривают одновременно с учетом диффузного и зеркального законов.
В этом случае результирующая вероятность перехода молекул газа через межлопаточные каналы или пазы с одной стороны рабочего колеса на другую
Ягпах = ®NKMax N (1 °N) Ягпах зер,
Где о'Л7 — коэффициент, учитывающий долю молекул, переходящих через рабочее колесо насоса и отражаемых при взаимодействии с поверхностью стенок межлопаточного канала или паза по нормали; 1 — AN — число молекул, переходящих через рабочее колесо и взаимодействующих с поверхностью стенок межлопаточного канала или паза по зеркальному закону.
Тогда
Яшах = Кг — Кц, (7.3)
А максимальное отношение давлений в рабочем колесе
Тшах = Кг/Ки- (7.4)
Здесь
|
|
Ki = отКт + (1 — Ki зер; Яц = OIlNKlIN + (1 — ст1Ш) Кц зер,
Где Ki, КЦ— вероятность перехода молекул газа через межлопаточный канал со стороны /—/ на сторону II—II и обратно; сгцу и о'п N—коэффициенты, учитывающие долю молекул, переходящих через рабочее колесо насоса соответственно со стороны /—/ на сторону II—// и обратно и отражаемых при взаимодействии с поверхностью стенок межлопаточного канала или паза по нормали.
Значения стш и ctIIw-приведены в работе [14]. На рис. 158, а—в приведены зависимости результирующей вероятности Кшах от u/vu при различных значениях а и Alb, определенные по уравнению (7.3), а на рис. 158, г— Е — зависимости ттах от Ulvn, Определенные по уравнению (7.4) для тех же значений а и Alb. В упрощенной теоретической модели (рис. 159), поясняющей процесс перехода молекул на противоположные стороны рабочего колеса, взаимодействие молекул газа со стенками межлопаточного канала рассматривают с учетом диффузного закона, при этом за направление отражения молекул принимают преимущественное, совпадающее с нормалью к поверхности стенок канала. Кроме того, скорости всех молекул газа принимают одинаковыми и равными наиболее вероятной скорости VB теплового движения молекул.
В этом случае результирующая вероятность перехода молекул через рабочее колесо
Ктах = (Ф/ ор — Ф// cp)/tt = Ki— Kin (7.5)
Где Ki = Фг ср/"; Кц— Фи ср
Углы срг и фн характеризуют вероятности перехода молекул через межлопаточные каналы рабочего колеса со стороны пониженного давления на сторону повышенного давления и обратно. Предполагая, что все молекулы, соударяющиеся с набегающей стенкой лопатки, переходят на сторону повышенного давления, а молекулы, соударяющиеся с уходящей поверхностью лопатки, переходят на сторону пониженного давления (рг = I = 0), средние значения углов
Ф/ ср = Yep + Рт ср5 Ф// ср = Yep — Pv ер, (7-6)
|
Рис. 159. Теоретическая модель перехода молекул газа через межлопаточные каналы рабочего колеса при постоянстве их скорости и отражении от поверхности каналов по нормали |
Где Yep = «------ In | (а/6)2 — (2A/b) cos а + 11 +
. /, cos а Г я, .
|
А/6- |
|
-cos а |
|
Sin а |
|
In2 a J |
|
■ arctg |
|
■ ( и ■ , f t coso w Pv cp = arcsin (__smaj + (l-------------------------------- ^-J X |
|
Arctg |
|
X |
|
1 — (u2/f2) sin2 a (h/%) sin a |
""К1 ф~) [T"a+arctg ■/"(a/ft —cos a)2 + (1 — «2/o|)sin
(ы/%) sin a
|
(iu/vH) Sin a Afb |
|
In |
|
+ |
■ cos a + i/^l — (ы2/г2) sin2 a
Alb — cos a + - yf (a/6 — cos a)2 + (1 — н2/»|) sin2 a
|
/ (alb - |
Cos а)2 + (1 - |
- н2/и2) sin2 а + U/VH (A/B — cos а) |
|
V (Ф - |
Cos а)2 +- (1 — |
H2/D2) sin2 а — M/DH (а/6 — cos a) |
|
2 a/b |
|
In |
|
J/ 1 — («2/f|) sin2 a — (U/VH) cos a |
|
Yf 1 — («2/f|) sin2 a + (M/fH) cos a |
|
In |
|
Тогда результирующая вероятность перехода молекул через рабочее колесо с учетом уравнения (7.5) |
Яшах = 2pV0P/Jt. (7.7)
Максимальную быстроту откачки колеса определяют по уравнению (7.2).
Максимальное отношение давлений в рабочем колесе насоса Ттах = ф/ ср/ф/; ср - (7.8)
Уравнения (7.7) и (7.8) для определения основных параметров откачной характеристики рабочего колеса насоса применимы при U/VH < 1,0 по принятому допущению.
В теоретической модели перехода молекул газа через межлопаточные каналы рабочего колеса, предложенной Савадой, Сузуки, Танигухи [23], принято диффузное отражение молекул от поверхности лопаток колеса, а также учтено влияние отраженных от корпуса насоса молекул на общее число молекул, проходящих через каналы рабочего колеса. Приведенные в работе результаты экспериментального исследования показали, что основные параметры откачной характеристики колеса насоса Sraax и тпшх с достаточной степенью точности могут быть определены и без учета влияния молекул, отраженных от корпуса насоса.
Для колеса с лопатками бесконечной длины коэффициент, учитывающий часть молекул, перешедших со стороны всасывания на сторону нагнетания,
+0,5 +0,5
M12 = m12-f | Тх2Их dx + j my2,uvdy,
—0,5 —0,5
Где M12 — вероятность перехода молекул со стороны I—I на сторону II—II без соударений со стенками межлопаточного канала, основные геометрические размеры которого, отнесенные к его длине, показаны на рис. 160; тх2, MV2 — вероятность того, что молекулы, отраженные от участка Dx или Dy, переходят на
сторону II—II; Uxdx, Иу Dy — доля молекул, соударяющихся с участком Dx Или Dy в единицу времени, из всего числа молекул, попавших в межлопаточный канал со стороны /—I.
|
/п12 |
|
F —С Sin бо — sin ene-*s cos2 Ml' 2 |
Вероятность перехода молекул
TOC o "1-3" h z S„ Г / —с Sin е,
= "2iT I ал^е-еои* 1+4- j е-'* Dtj
S=o L о /
Sine. -i
J Е-'2 Dt\ds,
N a
4 о
Где Sin 6i = — (s cos a — S^fa; cos 6x = Sin a/Г,; Sin 60 = — (s + Cos a)//•„; Cos 60 = Sin a/r0; rt — ]A(s cos a — S0)2 + Sin2 a ; R0 = ]/s + Cos a)2 + Sin2 a. Вероятность Mx2 Определяется По Уравнению
+0,5
Mx2 + J mX2F (x, y) dy = I — Dxl, -0,5
Где F (x, y) dy — доля молекул, соударяющихся в единицу времени с участком Dy, из общего числа молекул, отраженных от участка dx,
Ю, . . 1 Sin2 a ,
F(x, = °— 3/ dy,
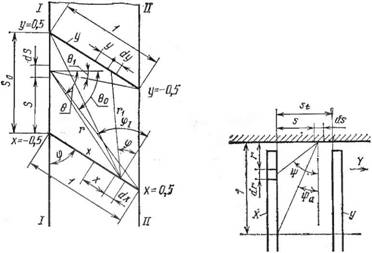
|
Рис. 160. Теоретическая модель перехода молекул через межлопаточный канал рабочего колеса |
|
Рис. 161. Схема, отражающая влияние соударений молекул газа с корпусом насоса на вероятность перехода через межлопаточные каналы рабочего колеса |
2 [(* + У + S0 cos a)2 + Sg sin2 a] '
|
.--и- |
DX1 — вероятность того, что молекулы, отраженные от участка dx, перейдут на сторону 1—1 без соударения,
Х + 0,5 + s0 cos a
_(х + 0,5 + su cos a)2 - f s2 sin2 a]I/2 . Вероятность Tny2 — 1 — Tnx2.
Произведение
Я
Их Dx = — Г ( °г— е-®8 sin (ср + а) + е*-с*cos' х
So J I V п
<Р=<Ро
/ ^ С Sin (<р+а) 1
X [с2 sin2 (ф + а) + - g-J I 1 + — J е-'1 Dt | cos ф Dcp Dx,
О
Где S0 = Arctg {[(x -{- 0,5) -J - s0 cos a ]f(s0 sin a)}.
Заменив в выражении для Uydx значения с = V/VH, А и х соответственно на —С, п — а, —У, получим выражение для Uxdy.
Таким образом, вероятность перехода молекул газа через рабочее колесо со стороны /—/ на сторону II—II при определенной относительной скорости = U/VH складывается из вероятности безударного прохода через канал и вероятности перехода молекул после соударений со стенками межлопаточного канала.
Вероятность перехода молекул со стороны I—I на сторону II—II для рабочего колеса с конечной длиной лопатки
Д f+0'5
М12 = Mi2 + (1----------- 2~) ( J т*2"ж dx +
V—0,5
+0,5 +0.5
+ J туфу Dy -F- -G- J M*X2 (Ux + Uy) dx,
—0,5 —0,5 J
Где A — коэффициент, учитывающий разность между числами столкновений молекул, отраженных от корпуса насоса, и столкновений молекул с элементарными площадками поверхностей х и у межлопаточного канала в единицу времени; т*2 — вероятность того, что молекулы, попавшие после соударения с корпусом насоса на участок Dx и отраженные от него, перейдут на сторону повышенного давления II—II.
Коэффициент
St / с — csinipo
А = sin a J ( - L J е-'2 Dt + sin фее"12 c°sS Ъ -L J Dt Ids,
S=0 О 0 '
Где ыпф0= —S/(s2+ 1),/2; cos ф0 = 1/(5®+ 1),/2 (рис. 161). Вероятность
Г)*
X2
Mh =
Здесь
Dh = (—sin +D** = 4"(sin Ф2+1),
|
Где |
X 4- 0,5 4- S0 cos a Sin q>i = — 1
|
Sin ф2 = — |
Ti Г/.. I n с I » „„о
[(* + 0,5 + So cos af + SQ sin2 a],/2 ' 1 — (x + 0,5 + S0 cos a) {[ 1 — (* + 0,5 + S0 cos a)]2 + SQ sin2 a}1/2 '
|
Отношение а/Ь
|
|
Вели |
Отношение Alb |
||||||||
|
Чины |
0,4 |
0,6 |
0,8 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
2,0 |
|
А =10°, сх= 1,6
|
|
Вели |
Отношение я/6 |
||||||||
|
Чины |
0,4 |
0.6 |
0,8 |
1,0 |
1,2 |
1.4 |
1,6 |
1,8 |
2,0 |
А = 20°, D^ 1,4
Ki 0,3982 0,5027 0,5877 0,6550 0,7061 0,7451 0,7754 0,7994 0,8189
/Сц 0,0333 0,0470 0,0603 0,0727 0,0889 0,1208 0,1676 0,2202 0,2722
Ктах 0,3650 0,4557 0,5274 0,5823 0,6172 0,6243 0,6077 0,5792 0,5467
Тгаах 11,96 10,69 9,750 9,013 7,945 6,167 4,625 3,630 3,008
|
А =20°, сх= 1,6
|
|
Вели |
Отношение а/Ь |
||||||||
|
Чины |
0,4 |
0,6 |
0,8 |
1.0 |
1.2 |
1.4 |
1.6 |
1,8 |
2,0 |
|
А |
= 30°, |
,2 |
|||||||
|
Ki Кп Km ах Тщах |
0,4831 0,0703 0,4128 6,870 |
0,5896 0,0946 0,4951 6,236 |
0,6688 0,1157 0,5531 5,780 |
0,7276 0,1348 0,5927 5,396 |
0,7704 0,1564 0,6140 4,925 |
0,8021 0,1859 0,6162 4,314 |
0,8262 0,2233 0,6029 3,700 |
0,8451 0,2647 0,5804 3,193 |
0,8602 0,3066 0,5536 2,805 |
|
А |
= 30°, |
Ci= 1,4 |
|||||||
|
Ki К11 '^тах Т-гаах |
0,5143 0,0635 0,4508 8,095 |
0,6245 0,0854 0,5392 7,317 |
0,7046 0,1042 0,6005 6,765 |
0,7623 0,1203 0,6420 6,339 |
0,8030 0,1372 0,6658 5,853 |
0,8321 0,1608 0,6713 5,174 |
0,8537 0,1928 0,6609 4,427 |
0,8703 0,2305 0,6398 3,776 |
0,8834 0,2702 0,6132 3,269 |
|
А |
= 30°, |
Cl = 1,6 |
|||||||
|
Ki Кп Ktnax ^max |
0,5362 0,0587 0,4775 9,138 |
0,6494 0,0787 0,5707 8,250 |
0,7306 0,0958 0,6348 7,629 |
0,7880 0,1097 0,6782 7,180 |
0,8275 0,1231 0,7044 6,720 |
0,8549 0,1416 0,7134 6,039 |
0,8747 0,1682 0,7065 5,199 |
0,8896 0,2016 0,6888 4,412 |
0,9012 0,2385 0,6628 3,779 |
|
А |
= 40°, |
Ci = 0,2 |
|||||||
|
Ki Кп К шах тшах |
0,3369 0,2401 0.0968 1,403 |
0,4165 0,3030 0,1135 1,375 |
0,4804 0,3558 0,1247 1,350 |
0,5348 0,4040 0,1308 1,324 |
0,5820 0,4500 0,1320 1,293 |
0,6228 0,4935 0,1293 1,262 |
0,6578 0,5336 0 1242 1,233 |
0,6877 0,5696 0,1181 1,207 |
0,7133 0,6016 0,1117 1,186 |
|
А |
= 40°, |
Ci = 0,4 |
|||||||
|
' ^ max Т-тах |
0,3883 0,2001 0,1882 1,940 |
0,4754 0,2550 0,2205 1,865 |
0,5433 0,3014 0,2419 1,803 |
0,5986 0,3446 0,2540 1,737 |
0,6444 0,3877 0,2567 1,662 |
0,6823 0,4303 0,2520 1,586 |
0,7139 0,4712 0,2427 1,515 |
0,7404 0,5090 0,2312 1,454 |
0,7624 0,5443 0,2191 1,403 |
|
А |
= 40°, |
А = о, б |
|||||||
|
^шах ''■max |
0,4366 0,1675 0,2691 2,607 |
0,5302 0,2151 0,3151 2,465 |
0,6009 0,2554 0,3459 2,353 |
0,6561 0,2931 0,3630 2,238 |
0,6997 0,3318 0,3679 2,109 |
0,7345 0,3721 0,3625 1,974 |
0,7627 0,4123 0,3503 1,850 |
0,7856 0,4508 0,3349 1,743 |
0,8047 0,4865 0,3182 1,654 |
|
А |
= 40°, |
C± = 0,8 |
|||||||
|
/Си К max TMax |
0,4781 0,1421 0,3360 3,364 |
0,5769 0,1836 0,3933 3,142 |
0,6495 0,2184 0,4311 2,973 |
0,7041 0,2507 (1,4535 2,809 |
0,7456 0,2843 0,4614 2,623 |
0,7775 0,3207 0,4568 2,424 |
0,8026 0,3589 0,4437 2,236 |
0,8227 0,3968 0,4259 2,073 |
0,8391 0,4330 0,4061 1,938 |
|
Вели |
Отношение а/Ь |
||||||||
|
Чины |
0,4 |
0,6 |
0,8 |
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
2,0 |
|
А = 40°,
|
|
Ci= 1,0 |
||||
|
0,7807 0,2455 0,5352 3,180 |
0,8104 0,2774 0,5330 2,922 |
0,8331 0,3123 0,5208 2,668 |
0,8510 0,3484 0,5026 2,443 |
0,8654 0,3840 0,4814 2,253 |
|
Ci= 1,2 |
||||
|
0,8049 0,2153 0,5897 3,739 |
0,8332 0,2421 0,5911 3,441 |
0,8545 0,2730 0,5815 3,130 |
0,8708 0,3064 0,5645 2,842 |
0,8839 0,3404 0,5434 2,596 |
|
Ci= 1,4 |
||||
|
0,8191 0,1924 0,6267 4,258 |
0,8470 0,2144 0,6326 3,950 |
0,8675 0,2409 0,6266 3,602 |
0,8831 0,2708 0,6123 3,261 |
0,8953 0,3025 0,5928 2,960 |
|
Cl= 1,6 |
||||
|
0,8247 0,1754 0,6493 4,701 |
0,8531 0,1933 0,6598 4,414 |
0,8736 0,2153 0,6583 4,058 |
0,8890 0,2417 0,6477 3,683 |
0,9010 0,2702 0,6308 3,334 |
Вероятность М21 перехода молекул через межлопаточный канал рабочего колеса на сторону пониженного давления определяется по уравнению для определения М12 при изменении знака относительной скорости на обратный.
Коэффициент, характеризующий максимальную быстроту откачки рабочего колеса при т = 1 (максимальный скоростной фактор),
ЕР1=Рг = Л*Is - М21; Kmax = К,- Ки, (7.9)
А максимальное отношение давлений при 6=0
Значения результирующей вероятности Ктах перехода молекул газа через межлопаточные каналы, имеющие различные геометрические параметры а и Alb при различных отношениях скоростей движения канала к наиболее вероятному значению тепловой скорости, а также максимального отношения давлений ттах, определенные по уравнениям (7.9), (7.10), приведены в табл. 7.1 [6].