РАСЧЕТ МОЛЕКУЛЯРНОЙ СТУПЕНИ НАСОСА ПРИ РАБОТЕ В МОЛЕКУЛЯРНОМ И ВЯЗКОСТНОМ РЕЖИМАХ ТЕЧЕНИЯ
При использовании молекулярных ступеней в комбинированных насосах в качестве промежуточных или последних ступеней пакета возможна их работа в молекулярном и вязкостном режимах течения. Для получения расчетных зависимостей основных параметров ступени рассмотрим теоретическую модель Геде.
|
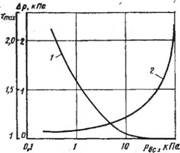
Рис. 148. Зависимость от давления всасывания молекулярной ступени 1 — максимального отношения давлений; 2 — разности давлений |
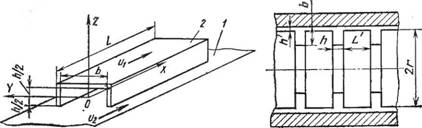
Заменив движение газа в канале ступени движением между двумя параллельными поверхностями 1 (рис. 149) и 2, движущимися со скоростями иг и иг в направлении оси ОХ, полагая, что
|
Рис. 149. Принцип действия молекулярного ва - Рис. 150. Расчетиая^схема куумного насоса молекулярного насоса Геде |
Скорости газа в направлениях, перпендикулярных оси ОХ, очень малы (Vy = vt = 0) и давление р постоянно в направлении 0Z, Перпендикулярном движущимся поверхностям, а также в направлении 0Y, получим
<Pvx _ 1 dp Dz2 ~ I] Dx'
Где г] — коэффициент динамической вязкости; Vx — скорость газа в направлении оси ОХ.
После интегрирования этого уравнения получим зависимость скорости газа по высоте канала между пластинами
Где Ct и С2 — постоянные интегрирования.
Расположим систему координат, чтобы плоскость X0Y была параллельна движущимся поверхностям и располагалась на равном расстоянии от них, т. е. на расстоянии z = Л/2.
При установившемся режиме течения газа условие равенства сил на слое газа, прилегающем к поверхности 1, от внешнего трения R = —е/ (oil — Mi) и внутреннего трения (вязкости)
8 (»Ж1 — щ) + г] = 0. Аналогично для слоя, прилегающего к поверхности 2: Е (vx2 — ы2) — = 0.
Где Е — коэффициент внешнего трения (сопротивления) газа о поверхность; V'xl, v'x2 — скорость газового слоя, прилегающего к поверхностям соответственно 1 И 2; F — площадь поверхности, на которой действуют силы трения.
Определяя V'X и V'X2 в соответствии с уравнением (4.2) 'для Z — Л/2 и Z — —H/2, уравнения равенства сил запишутся в виде
Из совместного решения этих уравнений
Г — «2 . г + иа Dp / H . H2
1 2tj/e + ft ' 2 2 йл; v 2e 8t] / •
Тогда уравнение (6.1) примет вид
+ 2r)/e + Л + "1+2Щ '
Количество газа, проходящее через поперечное сечение канала шириной B (в направлении 0Y, уг — г/2 = B), Ft/2
#Т , F , Mi + «2 !.«. Dp Bh* / H . I —h/2
Гдет — масса газа, кг; # — универсальная газовая постоянная, # = 8314 Дж X X кмоль-1- К-1; Т — абсолютная температура, К; М — молекулярная масса газа, кг/кмоль.
Подставляя в это уравнение зависимость коэффициента внешнего трения от давления
S = 6р,
Где 6 — констаита внешнего трения, для воздуха при 293 К 6 = 1,61- Ю-4 с/м, И интегрируя по длине канала от хг до х2, для которых р равно соответственно р1 и р2, определяют выражение, связывающее между собой геометрические, скоростные и откачные параметры канала:
_ ____ Ft2 , , Г H L MRTh "1
** 6N(Ml + "2) (Pi~P*>+IB(U1 + U2) ' Mb3/T («х + иа)г J X
TOC o "1-3" h z , P1-2mRT/Mbh(u1 + ui) (R ™
A p2 — 2mRT/Mbh (ux + Иа)' У >
Из этого уравнения следует, что максимальное количество газа, откачиваемое каналом при равенстве давлений рг = р2 = р,
M = Mbhp (иг + uz)/2RT (6.3)
И максимальная разность давлений при M = О
Где L — длина канала, L = хг — х2-
Это уравнение учитывает влияние сил вязкости и внешнего трения в зависимости от режима работы, т. е. от р. При больших давлениях второе слагаемое правой части этого уравнения существенно меньше первого слагаемого, т. е. для большого давления (вязкостное течение)
(Pi — P2)max = 6т]L (иг + U2)/h2
Или для канала молекулярной ступени при иг = О
(Pi — Рг) шах = 6г]Lu/H*
Разность давлений постоянна и не зависит от абсолютного значения р.
При малых давлениях (режим течения газа, близкий к молекулярному) первое слагаемое будет пренебрежимо мало по сравнению со вторым
M"i + "a) = или, так как их = О,
Pi - г _„/.«е/й
~~Z — lmax — с
Р 2
Учитывая перетекания газа через зазоры из одного канала в другой [уравнение (6.2)] (рис. 150), максимальное отношение давлений находят из уравнения
А (ттах + -L. _ 2 ) + В (тгаах - 1) - С lg ттах + lg2 тшах = 0, (6.4)
1шах /
Где А = (2Nrh'f/L'b (2,303Ft)2; В = S'wh'Q (2Nrf/b (2,303/г)2 [w — частота вращения ротора; S' = (26 Fc)/(2Jv)]; С = (щ ы2) 2лг0/2,303Ft = ^ = = 2Zi (Г — 6/2) W]; величины Ft', L', 6, г и Ft пояснены иа рис. 150.
Таким образом, в зависимости от заданной быстроты откачки S молекулярной ступени выбирают геометрические параметры канала H и B (B > 5H) при условии обеспечения Smax > (5 ... 10) S из уравнения (6.3) и допустимой скорости движения и на внешней поверхности рабочего колеса. Скорость и ротора молекулярной ступени, используемой в комбинированном насосе, определяется размерами и частотой вращения высоковакуумной части пакета, т. е. равна допустимой скорости и% на наружном диаметре рабочих колес турбомолекулярного насоса. Длина L канала молекулярной ступени равна длине внешней окружности ротора молекулярной ступени.
По уравнению (6.2) или (6.4) в зависимости от режима течения газа рассчитывают создаваемую разность давлений или отношение давлений.
Число молекулярных ступеней определяют исходя из условия обеспечения сжатия газа от давления, обеспечивающего работу рабочих колес турбомолекулярного насоса в молекулярном режиме течения (около 0,1 Па), до давления около 103 Па, где эффек-
|
Стики молекулярной ступени: I — при = 10® Па (вязкостный режим течения); II лярный режим течения). Порядок расчета представлен в виде табл. 6.1. |
Щ-10* Я,98-ю* $9710* д,96Ю*рьЛа
Тивность молекулярных ступеней резко снижается. При достижении давления после молекулярных ступеней более 103 Па следует использовать вихревые ступени.