ВАКУУМНЫЕ ПОРШНЕВЫЕ НАСОСЫ

Профилирование роторов. Расчет зазоров

При профилировании роторов решают задачу: по выбранной части профиля построить сопряженную с ней часть другого про­филя. Задача профилирования решается для теоретических про­филей, т. е. профилей, между которыми нет зазора.

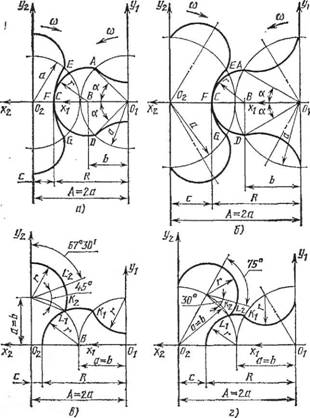
Профили роторов двухроторных вакуумных насосов характе­ризуются следующими размерами (рис. 62), которые связаны соотношени ями:

Для ротора с Z = 2

А = Jt/(2Z) = 45°, г = R - Ь, с = 2а—г, B=(Ra—Aa)/(2tf—А/2); для ротора с Z = 3

А = n/(2Z) = 30°, г = R — Ъ, с = 2а — г, Ь = (Я2 — о3)/ (27? — с/ 3),

Где Z — число лопастей; г — радиус головки ротора, м; R — наружный радиус ротора, м; с — ширина впадины ротора, м; а — радиус начальной окружности, м; Ь — расстояние от центра ротора до центра окружности, которой описана го­ловка ротора, м.

Профили роторов двухроторных вакуумных насосов выпол­няют двух типов: окружные и циклоидально-окружные.

Окружные профили — это профили, в которых головка ротора описывается окружностью радиуса г (рис. 62, с и б), центр В Которой расположен от оси Ot ротора на расстоянии Ъ, меньшем или равном 0,9288с для двухлопастных и 0,9670а для трехлопа­стных роторов.

Циклоидально-окружные профили — это профили, в которых головка ротора частично описана окружностью радиуса г (рис. 62, в и г), центр которой расположен от центра ротора Ot На расстоянии Ь, большем 0,9288а для двухлопастных и 0,9670с для трехлопастных роторов, и эпициклоидой KiLlt которая описывается точкой Кч при качении без скольжения окружности радиуса а с центром в точке 02 по окружности радиуса а с центром в точке Ог.

Окружные профили характеризуются одним из следующих соотношений: для двухлопастных роторов Ь/а = 0,5 ... 0,9288; R/A = 1,2368 ... 1,6698; с/а = 0,7632 ... 0,3302; для трех­лопастных роторов Ь/а = 0,5 ... 0,9670; R/A = 1,1196 ... 1,4770; С/а = 0,8804 ... 0,5230. При этом профили описываются плавной выпукло-вогнутой кривой, на которой отсутствуют точки пере­гибов и петли.

Обычно выбирают большие значения отношений Ь/а и R/A И меньшие значения отношения с/а, так как при этом площадь Fv Торцового сечения ротора получают меньше, а коэффициент % = = 1 — 77p/(jtjR2), оценивающий качество профиля, больше. Чем больше значение коэффициента %, тем меньше размеры и масса вакуумного насоса для заданных условий работы и быстроты действия. Однако при больших значениях коэффициента % ухуд­шаются прочностные характеристики ротора, поэтому при расчете профиля ротора его рассчитывают на прочность.

В двухроторных вакуумных насосах вследствие перепада давления сила, действующая на роторы, мала по сравнению с центробежной силой, поэтому роторы рассчитывают на разрыв от действия центробежной силы (Н):

/?ц = 0,5Уррсо27?ц. Т1

Где Vp — объем ротора, м3; р — плотность материала, из которого выполнен ро­тор, кг/м3; со — угловая скорость ротора, рад, to = 2пп (П — частота вращения ротора, с-1); т — расстояние от оси ротора до центра тяжести половины ро­тора, м.

Напряжение на разрыв, действующее в центральном сечении впадины, (МПа)

А = R4/[2L (с — DJ2) ],

Где L — длина ротора, м; jDB — диаметр вала под ротором, м.

Коэффициент запаса

П3 = aja,

Где от — предел текучести при сжатии для материала, из которого выполнен ро­тор, МПа.

Сопряженный профиль строят на плоскости, так как по длине ротора его профиль не меняется. В винтовом роторе профиль без изменений поворачивается на угол и' = x//L, где L — длина ро­тора, м; / — расстояние от торца, на котором угол закрутки принят за нуль, до рассматриваемого сечения, м.

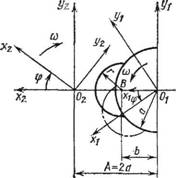
Построение профилей проводят в подвижных системах координат Х101у1 и х202у2 (рис. 63). Система координат ХхОхух жестко связана с первым ротором, центр ее Ох со­впадает с осью ротора, угол ср пово­рота — с углом поворота ротора. Система координат х202у2 жестко связана с сопряженным ротором, центр ее 02 совпадает с осью сопря­женного ротора, угол ф поворота — с углом поворота сопряженного ро­тора.

Углы ф поворота роторов равны, так как роторы вращаются с одина­ковой угловой скоростью со. Рас­стояние между центрами координат Oi и 02 равно межцентровому расстоянию между роторами А = = 2а, м. Системы координат Х101у1 и х202у2 связаны между со­бой уравнениями:

Х2 = —A cos ф Хх cos 2ф - f - ух sin 2ф; у2 = A sin ф — Хх sin 2ф - f - уг cos 2ф.

В системе подвижных координат ХхОхУх записывают уравнение окружности, которой описана головка первого ротора:

Хх = b - f - г cos ф;

(3.1)

У — — F sin ф,

Где |) — параметр окружной части профиля, за который принят угол между об­щей нормалью к сопряженным профилям в точке их касания и положительным направлением оси 01х1.

Сопряженную часть (впадину) другого профиля получают построением огибающей в системе подвижных координат х202у2. По данным И. А. Сакуна, для этого уравнение (3.1) из системы подвижных' координат ХхО^х переписывают в систему подвижных координат х202у2:

Х2 = —A cos ф -[- (b - f - г cos xj)) cos 2ф (—г sin sin 2ф; У2 = A sin ф — (B + г cos я]з) sin 2ф + (—Г sin я]з) cos 2ф,

И записывают функциональный определитель, который раскры­вает связь между углом ф поворота координат в направлении вра­щения роторов и параметром я]з профиля:

1д(х2, у2)У[д{Ф, -ф)] = 0.

Раскрывая скобки и приводя подобные члены, получим: Х2 = — A cos ф + B cos 2ф + г cos (ф + 2ф); )

У2 = A sin ф — Ъ sin 2ф — г sin (ф + 2ф); [д(х2, у2)/[д (Ф, - ф)] = = a sin ф cos — (b — a cos ф) sin яр = 0.

При построении сопряженного профиля углом ф задаются произвольно, угол г]; получают из уравнения (3.3), координаты со­пряженной части профиля в системе координат х202у2 определяют по уравнению (3.2). Так как профили роторов в двухроторных вакуумных насосах одинаковы, то полученную сопряженную часть достраивают к головке ротора, которая описана окружно­стью радиусом г, и получают профиль ротора.

Расчет циклоидально-окружных профилей выполняют анало­гично, но циклоидально-окружные профили получают при соот­ношениях: для двухлопастных роторов Ыа > 0,9288, R/A > > 1,6698, с/а < 0,3302; для трехлопастных роторов Ыа > 0,9670, R/A > 1,4770, с/а < 0,5230. При данных соотношениях коэффи­циент х получается больше, чем для роторов с окружным профи­лем, т. е. на одни и те же условия работы и одинаковую быстроту действия вакуумные насосы, имеющие роторы с циклоидально - окружными профилями, получаются по размерам и массе меньше, чем вакуумные насосы, имеющие роторы с окружными профилями.

Однако в роторах с циклоидально-окружными профилями получается небольшая ширина с впадины ротора и ротор не об­ладает достаточной прочностью, т. е. во всех случаях, когда полу­чают прочный ротор, целесообразно применять циклоидально - окружные профили.

С технологической точки зрения наибольший интерес пред­ставляют роторы с отношениями: для двухлопастных роторов B/A = 1, R/A = 1,7654, с/а = 0,2346; для трехлопастных роторов Ыа = 1, R/A = 1,5176, с/а = 0,4824. В этом случае центр окруж­ности радиусом г, которой описана головка профиля, лежит на начальной окружности радиуса с, т. е. b = с. Уравнение этой окружности в системе координат х^ОуУх.

(3.4)

Сопряженная часть другого профиля в системе координат Х2Р2У2'

Х2 = —A cos ф + (й 4- г cos - ф) cos 2ф + (—Г sin я]з) зт.2ф;

У2 — A sin ф — (а г cos - ф) sin 2ф + (—r sin 'Ф) cos 2ф. При у = 0 получим

Х2 = —а + гсоэф; у2 = —г Sin яр

И функциональный определи­тель

[д (*2, YJV'Ld (Ф, =

=sin (tp + - ф)—sin - ф=0. (3.6)

При ф = 0 функциональный определитель обращается в тож­дество, т. е. параметр я]з профиля может принимать любые значе­ния, а уравнение (3.6) будет тождественно удовлетворяться. Это указывает на то, что при Ф=0 сопряжение теоретических профилей происходит одновре­менно всеми точками, располо­женными внутри окружности радиуса а в системе координат

Нения одной и той же окружно­сти, но заданные в разных си-

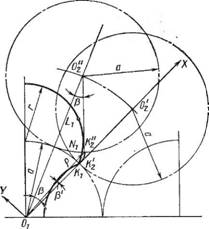
Стемах координат. При ф Ф 0 все точки окружности радиуса г, которой описана головка профиля, одновременно выходят из заце­пления с точками окружности того же радиуса, которой описана впадина сопряженного ротора, и между ними образуется зазор. При построении сопряженной части профиля при циклоидаль­но-окружном профилировании в месте перехода впадины в го­ловку появляется острый перегиб в двухлопастном профиле при Ыа = 0,9288 и трехлопастном профиле при Ыа = 0,9670, а при больших отношениях Ыа — петли на участках K-J^y и K2L2 (см. рис. 62, виг). При обработке петли срезаются и при обкаты­вании профилей в этом месте появляется недопустимо большой зазор, что приводит к увеличению перетекания газа. Чтобы уменьшить этот зазор на участке (рис. 64) от начальной ок­ружности радиусом а (точка Кг) до окружности радиусом г (точка Lt), которой описана головка ротора, профиль выполняют по эпициклоиде, которая образуется точкой К2 (одним штрихом обозначено начальное положение, двумя — промежуточное) при качении без скольжения окружности радиусом а с центром в то­чке 02 по окружности радиусом а с центром в точке Ог. Начальная точка эпициклоиды К'а совпадает с точкой К, промежуточная точка К.2 не совпадает с точкой NЬ а отклоняется от нее на рас­стояние NxKZ = е; последняя точка эпициклоиды совпадает с точкой LX, т. е. эпициклоида лежит снаружи окружности KJNJLJ Радиусом г. Отклонения е (мкм) эпициклоиды от окружности ра­диуса г для трехлопастного ротора приведены в табл. 3.1.

При применении на участке эпициклоиды при обкатыва­нии роторов точка К одного ротора будет скользить по эпицик-

Лоиде другого ротора и наоборот, т. е. для теоретических профилей на участках /С^ и зазор будет равен нулю, как и для всех остальных участков теоретического профиля. Для номинальных профилей на участке будет сохраняться постоянный задан­

Ный зазор брр. Уравнение эпициклоиды в системе коорди­

Нат хОгу запишется в форме

Х = а (2 cos Р — cos 2|3); У = а (2 sin Р — sin 2|3),

Где Р — параметр эпициклоидальной части профиля, за который принят угол поворота производящей окружности радиусом а, точка К2 на которой описывает данную эпициклоиду; при построении профиля углом р задаются.

Радиусы-векторы р (рис. 64) точек эпициклоиды КгЬг и их углы (У определяют по формулам:

Р = / у2; р/ = arctg (у/х).

Для того чтобы в процессе работы роторы не заклинило, при проектировании между роторами, роторами и корпусом, роторами и торцовыми крышками необходимо предусмотреть за­зоры, которые компенсируют неточности изготовления и сборки вакуумных насосов, удлинения роторов, корпусов и изменение межцентрового расстояния вследствие нагрева деталей вакуум­ного насоса при работе и деформаций деталей, вызванных дей­ствием на них сил при работе.

Зазоры брр между роторами и брк роторами и корпусом обес­печивают путем занижения профилей роторов в торцовом сечении на величину брр/2, т. е. путем построения эквидистанты профиля, которую называют номинальным профилем.

Для номинального профиля головку описывают радиусом rK = г — 0,5брр. При окружном профилировании размеры со­пряженной впадины определяют по уравнениям (3.2), в которых вместо значения г подставляют значение г + 0,5брр, а уравнение (3.3) при этом остается без изменения.

При циклоидально-окружном профилировании радиус, кото­рым описывается впадина, определяют по зависимости ги = г + + 0,5брр; ширину впадины по зависимости си = с — 0,5брр;

Координаты точек эпициклоиды KiL^ (см. рис. 62, в и г) рассчи­тывают из соотношений:

Хн = х —|- [0,56рр (cos 2|3 — cos Р)]/^2 —cosP;

Ун = У + [0,56рр (sin Р — sin2Р)]/>/ 2 — cos р.

Пределы изменения угла Р: для двухлопастных роторов 0 < < Р 45° и для трехлопастных роторов 0 < Р 30°.

Монтажный зазор между роторами (профильный зазор)

Брр mm = | Atfmin 1/2 + I A (2c)min 1/2 + | ДЛт1п | + Ас + AR - ДЛ, тогда максимальный зазор между роторами при работе

Ирр max — |Д£тах|/2 + А(2с) max 1/2 +1 ДЛ max р

Где ADmin, ADmax, Acmin, Астах, АЛrain, АЛП1ах—минимальные и максимальные допуски на диаметр, ширину впадины ротора и межцентровое расстояние при из­готовлении; Ас — увеличение ширины впадины за счет нагрева ротора, Ас = = арС А^р (ар — коэффициент линейного расширения материала ротора; Atp = = <р — TB, Tp — температура ротора в рабочем состоянии); AR = A^R Д^p, AR — удлинение ротора в радиальном направлении в рабочем состоянии; АЛ — увеличение межцентрового расстояния в результате нагрева крышек, в которых расположены подшипники, АЛ = а Л A T (а — коэффициент линейного расшире­ния материала крышек подшипников; AT = п— T0, T1; п — температура крышек подшипников в рабочем состоянии; T0 — температура окружающей среды).

Для вакуумных насосов, работающих при давлениях всасы­вания 1,33 ... 133,3 Па, на основании опытных данных принимают At = 40 ... 60°; для вакуумных насосов, работающих при дав­лениях всасывания 75 ... 100 кПа, At = 80 ... 100°.

Монтажный зазор между корпусом и ротором (радиальный зазор)

Бр. К mm = I ADmln 1/2 + I ДDK min |/2 - ARK + AR + (ДЛ)/2,

А максимальный радиальный зазор при работе

Бр. к max = | АГ)тах |/2 + | ADK max |/2,

Где ADK mIn, AD,,. max—минимальное и максимальное значения допусков на диа­метр расточки при изготовлении корпуса; ARK — удлинение корпуса в радиаль­ном направлении в рабочем состоянии, ARK = ак/?к А^к (ак — коэффициент линейного расширения материала корпуса; AfK = T,; — Tn, T1; — температура корпуса в рабочем состоянии).

Для вакуумных насосов, работающих при давлении всасы­вания 1,33 ... 133,3 Па, на основании опытных данных принимают Д/к = 40 ... 60°, = 70 ... 100 °С; для вакуумных насосов,

Работающих при давлении всасывания 75 ... 100 кПа, AtK = = 80 ... 100°, Atv = 130 ... 150 °С.

Монтажные торцовые зазоры со стороны плавающей опоры

Бт. пл mm = 0,5 (IДLmln I +1ALK MIn I) + AL — ALK;

Со стороны жесткой опоры

Бт. ж тт = 0,5 (| ALK MIn | | ALmIn I),

Где ALmm. AL„ mIn —минимальные значения допусков на длину при изготовлении ротора и корпуса; AL = apL Afp (L — длина ротора, м); ALK = aKLK AfK (LK — длина корпуса, м).

Максимальные торцовые зазоры при работе со стороны жест­кой опоры

Ж шах = 0,5 (| ALK max | | ALmax |)>

Со стороны плавающей опоры

Пл шах = 0>5 (| ALK шах | I ALmax |),

Где AZ-к шахи ALmax — максимальные значения допусков на длину при изготов­лении корпуса и ротора.