ВАКУУМНЫЕ ПОРШНЕВЫЕ НАСОСЫ

ДИНАМИЧЕСКИЙ РАСЧЕТ

Для нахождения механических потерь и сил, действующих на основные детали насоса, определяют скорости и ускорения пластин.

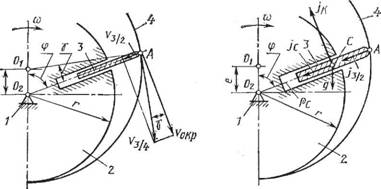
Скорость пластины. Пластина насоса участвует в сложном вращательно-поступательном движении. Окружная скорость конца радиальной пластины (точка А, рис. 41) с учетом уравнения (2.14) (м/с)

Иокр = рсо = Rv> (1 + Я cos ф — 0,5Я sin2 ф),

Где ф — угол поворота пластины, рад.

Скорость радиальной пластины относительно ротора (м/с)

Сз/2 = = — ею sin ф (1 Я cos ф) = — ею (sin ф - J - 0,5Я sin 2ф).

Знак «—» показывает, что вектор скорости направлен к центру ротора.

Полная скорость конца пластины, направленная - по окруж­ности, (м/с)

7 Cosy l-0,5fr>sin «Ф/

Скорость конца пластины относительно разгрузочных колец (скорость скольжения пластин относительно колец) (м/с)

Уз/1 = Уз/4 - Я сок = Яю (1 +-------------- ^----------------- , (2.37)

1 — 0.5Я,2 sin2 ф « J

Где cdj, — угловая скорость разгрузочного кольца, рад/с.

Рис. 41. Схема расположения скоро­стей пластины в точке соприкосновения с корпусом:

1 — ось ротора; 2 — ротор; 3 — пластина; 4 — корпус

Знак «+» соответствует направлению вектора скорости »з/1 В сторону вращения ротора.

Разгрузочные кольца насосов обладают большой массой и мо­ментом инерции. Например, разгрузочное кольцо вакуумного насоса РВН-50 имеет массу 30 кг и динамический момент инерции 9 кг-м2. На его внутреннюю поверхность при вращении действуют непрерывно изменяющиеся моменты от сил трения со стороны пластин с частотой F = 162 Гц, пропорциональной частоте вра­щения ротора и числу пластин. Расчеты, подтвержденные экспе­риментом показали, что разгрузочные кольца обычно вращаются практически равномерно, причем частота их вращения близка к частоте вращения ротора.

Для рекомендуемых значений коэффициентов трения и соот­ношений геометрических размеров в насосах скорость скольже­ния пластин по кольцам г;з/i непрерывно изменяется по величине и направлению вследствие того, что разгрузочные кольца вра­щаются равномерно, а скорость концов пластин непрерывно из­меняется. При одинаковой в данном направлении скорости конца пластины и кольца скорость »3/i = 0, причем пластина в этот момент расположена под углом ф0 к вертикальной оси на­соса. Следовательно, при угле поворота пластины от ф = —ф0 до ф = ф0 концы пластин обгоняют разгрузочные кольца и пере­дают им энергию, а на остальном участке от ф = ф0 до ф = 2я — — ф0 разгрузочные кольца обгоняют пластины и частично воз­вращают энергию ротору.

Угловую скорость кольца определяют из формулы (2.37) при »з/1 = 0 (рад/с):

Обычно угол ф0 находится в пределах ф0 « 75 ... 80° [11], а угловая скорость разгрузочного кольца превышает угловую скорость ротора: шк = (1,04 ... 1,06) со. При заклинивании раз­грузочных колец пластины скользят по кольцам в одном направле­нии в течение всего оборота ротора, а угол ф0 отсутствует.

При выборе допустимой скорости скольжения пластин обычно исходят из допустимого износа пластин. Средняя окружная скорость стальных пластин (сталь 85), опирающихся на враща­ющиеся разгрузочные кольца из чугуна СЧ 20, не превышает 12 ... 13 м/с. Средняя скорость скольжения текстолитовых (ПТ-7) и асботекстолитовых пластин (марки А) по чугунному корпусу находится в пределах 11 ... 15 (18) м/с при подаче масла на сма­зываемые трущиеся поверхности. Средняя скорость скольжения по стальному корпусу графитовых пластин (УГ-20к, АГ-1500-Б-83 и др.) не более 8 м/с, а пластин из антифрикционной фторопласто­вой композиции (ФКН-7)—6 ... 8 м/с.

Ускорение пластин. При равномерном вращении ротора на пластину действуют ускорения в продольном и поперечном на­правлениях (рис. 42).

Центростремительное ускорение в радиальной пластине дей­ствует вдоль радиуса ротора и приложено к ее центру тяжести в точке С (м/с2):

/с = — Рс«Л

Где рс — радиус-вектор центра масс пластины, м, рс = 02С.

Полагая, что центр тяжести пластины расположен в ее сере­дине, находим

Рс = Р-------- + ЯсОБф — -|-81П2ф —щ) •

Знак «—» показывает, что ускорение направлено к центру ротора.

Ускорение радиальной пластины относительно паза ротора (м/с2)

Dvom d2p

Hn = —^f - = ф = —еау1 (cos <p + I cos2 ф).

При постоянной угловой скорости ротора и изменении поло­жения центра тяжести пластины возникает поперечное ускорение (ускорение Кориолиса). Оно приложено к центру тяжести пла­стины перпендикулярно ее плоскости и направлено в сторону, противоположную вращению ротора (м/с2):

/к — 2еа>2 ^sin ф -(- sin 2ф) .

Кроме перечисленных ускорений, на пластину действуют также ускорения силы тяжести, которые можно не учитывать ввиду их малости.

Скорости и ускорения для наклонных пластин определяют по аналогичным зависимостям.

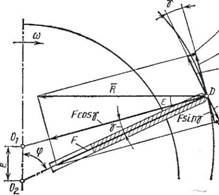
Усилия, действующие на пластину. При работе насоса на его пластину действуют четыре вида сил: силы инерции, реакции опор, силы трения и газовые усилия. Продольную силу F, дей­ствующую вдоль радиальной пластины и направленную от центра ротора, можно разложить на нормальную силу F cos 7 и каса­тельную силу F sin Действующие на пластину силы могут быть разложены на продольное к оси пластины направление и попереч­ное ей. Схематическое расположение сил, действующих на ра­диальную пластину со стороны корпуса при угле ф поворота ротора, изображено на рис. 43.

Принимают следующее правило знаков для сил: поперечная сила положительная, если она направлена против движения; продольная сила положительная, если она направлена от центра ротора.

Поперечная составляющая от касательной силы (Н)

Ri = ±F cos 7 sin У.

Знак «—» относится к углу поворота пластины от 0 до я, а знак «+» — от л до 2л.

При отсутствии сил трения между пластиной и цилиндром реакция цилиндра направлена к его центру (в точку 0Х). С учетом сил трения реакция цилиндра R отклоняется от радиуса цилиндра в сторону вращения ротора на угол е трения, причем

(ijjF cos v

F cos v F cos y где (г,, — коэффициент трения пластины о корпус иасоса.

В предварительных расчетах для стальных пластин (сталь 85) со смазочным материалом, опирающихся на чугунные разгрузоч­
ные кольца (СЧ 20), коэффициент трения задают в пределах р2 « 0,06 ... 0,08 (0,1) [11]. Для асботекстолитовых пластин (мар­ки А), скользящих по чугунному корпусу (СЧ 20) со смазыванием, при температуре на нагнетании не выше 370 К коэффициент трения определяют по эмпирической фор­муле [11]

0,165 Lg (и — 0,5) '

Где и — средняя скорость скольжения конца плас­тины по корпусу, м/с;

При смазывании цилиндра вязкими мас­лами (типа МК-22п)

Р2 « 0,103 (lg и)—°-ш; (2.38)

При смазывании цилиндра маслами малой вязкости (типа веретенного АУ)

Р2 « 0,0945 (lg ы)~М61.

А для графитовых пластин (АГ-1500-Б-83), скользящих по корпусу из высоколегированной стали без смазывания, коэффициент р2 л; « 0,2.

Сила FrР трения при отсутствии беговых колец направлена в сторону, противоположную направлению вращения ротора, а если пластины опираются на разгрузочные кольца, то направ­ление силы трения противоположно направлению вектору ско­рости vz/i скольжения пластин относительно колец. Поперечная составляющая силы трения (Н)

= F-гр cos у = p2F cos2 у.

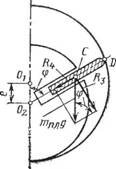
Поперечная составляющая веса пластины (Н) (рис. 44) Rs = — mnjIg sin ф,

Где /япл— масса пластины, кг; g — ускорение свободного падения, g — 9,81 м/с2.

Интенсивность разгрузки от поперечных инерционных сил ускорения Кориолиса (Н/м)

Q1 = — mnnjK/h = 2тпле(о2 (Sin Ф + Х/2 Sin 2ф)/h, Где h — ширина пластины, м.

Интенсивность нагрузки от перепада давлений газа на вы­ступающую часть пластины (Н/м)

<?2 = A PL,

Где Ар — перепад давлений между двумя соседними ячейками, Па.

Перепад давлений Ар между двумя соседними ячейками учи­тывается только лишь в процессе сжатия газа и обратного рас­ширения. Часто в предварительных расчетах перепад давлений на участке обратного расширения принимают равным нулю.

Стины, которая воспринимает перепад давлений, рад.

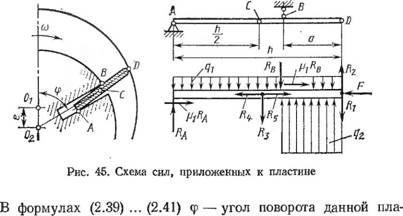
Реакции пластины в пазу ротора определяют из уравнений статики, предложенных В. Д. Лубенцом. Схема расположения сил приведена на рис. 45, где ячейка находится на углу сжатия газа. Реакции пластин в т. А и В (Н)

+ (sin у cos Y + р2 cos2 у) F];

2(ft-a) +

Rs + ЦФ —Л-------- Ь 2 (sin у cos "у + Н-2 cos2 V) F>

Где a — выступающая из ротора часть пластины, м.

Продольная сила от центростремительного ускорения и уско­рения пластины относительно ротора (Н)

Rb = — тпл (/с + /3/2).

Продольная составляющая веса пластины (Н)

Ri = —тпл§ cos ф.

Сила трения пластины в пазу ротора (Н)

F'vP = ±ih(Ra + RB), (2.42)

Где — коэффициент трения пластины о паз ротора, « 0,08 ... 0,1.

Знак «+» относится к углу поворота пластины от 0 до я, а знак «—» от л до 2л. Знак в формуле (2.42) учитывается коэффи­циентом А = sin ф/| sin ф |:

F'TP = Лр,(| + |).

Эта формула справедлива при всех значениях угла ф поворота ротора, за исключением ф = 0 и я. Однако при этих углах пово­рота сила трения F'TV = 0, так как скорость перемещения пластин в пазах ротора 1/3 2 = 0.

Суммарная продольная сила определяется как сумма сил (Н):

F = R4 + R5 + F'tp. (2.43)

При ф = 0 и я продольная сила (Н)

F = Я4 + R5.

Подставив значения RA и RB и решив уравнение (2.43) отно­сительно F, получим

Р ^ Ri + R& + Hi W(h — a)] (gift + Rs) + Hi lh/(h — a)] g2a 1 — (sin v cos v + F-2 cos2 v) [ (ft + O)l(h — A)]

Необходимо отметить, что в данном расчете ввиду малых значений не учитывают продольные силы: [x2F cos 7 sin 7 и F sin2 у, а также моменты от сил трения пластин в пазу ротора:

МА = ц^б и Мв = р^б, где б — толщина пластины. При этом ошибка не превышает 1 ... 1,5 96.