ТЕХНОЛОГИЯ МИНЕРАЛЬНЫХ УДОБРЕНИЙ

О ГЕОМЕТРИИ ГАЗОВОГО ФАКЕЛА В ПРОЦЕССЕ ПОЛУЧЕНИЯ ГРАНУЛИРОВАННЫХ УДОБРЕНИИ В ПСЕВДООЖИЖЕННОМ СЛОЕ

Одним из перспективных способов получения гранулиро­ванных минеральных удобрений является использование ап­паратов псевдоожиженного слоя. Техника псевдоожижения, с необычайной быстротой внедрившаяся в ряд отраслей про­мышленности, открывает широкие перспективы для произ­водства гранулированных удобрений. Однако вопросы гра­нулирования в псевдоожиженном слое изучены в настоящее время далеко не достаточно. Богатой и разносторонней прак­тике, как это часто имело место в истории техники, проти­востоит недостаточная полнота теоретических исследований. В основу разработанных математических моделей процесса гранулирования химических продуктов в аппаратах кипяще­го слоя [1—5] положены следующие физические представле­ния [1]: распыленные пневматической форсункой капли рас­твора гранулируемого продукта движутся в факеле газовой струи, участвуя в то же время в процессе массообмена сушка, нейтрализация). При этом принимается допущение, что факел струи в кипящем слое согласно гипотезе Шаховой [7] состоит из двух зон: чисто газовой и двухфазной, состоя­щей из газа и присоединенных частиц слоя (граница зон определяется скоростью свободного витания частиц).

Осаждаясь на гранулах слоя, капли растекаются по их поверхности тонкой пленкой раствора. Под действием тепла ожижающего агента влага, содержащаяся в растворе, выпа­ривается, из него выкристаллизовывается гранулируемый ма­териал, который и дает приращение массы гранулы.

Стабильность технологического режима работы грануля­тора во многом определяется параметрами работы распыли - вающего устройства и, в частности, геометрическими харак­теристиками факела форсунки. При этом одними из наибо­лее важных величин являются максимальный радиус и даль­нобойность газового факела, определяемые по формулам

_ Гэ, в"о' . 1 f frr <1 (2V

Хф' 0.366C2uBI1T V 0,5Рсл

Где «о, "m* — скорость газового потока: начальная, в макси­мальном сечении струи, м/с; ивит — скорость витания части - слоя, м/с; Гэкв — эквивалентный радиус сопла форсунки, м; Рг, рсл — плотность: газа, слоя, кг/м3; и — начальная концен­трация струи, кг раствора/кг распыливающего воздуха; С і, С2 — коэффициенты.

Уравнения (1) и (2) дают хорошее совпадение с экспери­ментальными данными при известных из опыта коэффициен­тах Сі и С2. А. Г. Минаев [8] считает, что значения этих ко­эффициентов определяются только гидродинамикой слоя и могут быть рассчитаны по уравнениям

Ci=0,81Ar~0,115Re0'32; (3)

Где Аг и Re — критерии Архимеда и Рейнольдса для частиц слоя; р'п — плотность пограничной зоны «газ — твердые ча­стицы» факела струи, кг/м3. Коэффициент С\ характеризует динамику изменения газовой зоны, а коэффициент С2 — зоны «газ — твердые частицы» по длине факела.

Ранее [6] нами было показано, что уравнение (4) не имеет физического смысла. Действительно, истечение свобод­ной затопленной струи является частным случаем истечения струи В псевдоожиженный СЛОЙ (при Рсл —рг) - Поэтому при рсл->-рі - коэффициент С2 должен стремиться к нулю (отсут­ствие частиц в струе). Однако при расчете коэффициента С2 по выражению (4) этого не происходит. В связи с этим воз­никает необходимость в уточнении расчетной формулы для определения величины С2.

Как известно [1, 3, 4], газовую струю, истекающую в псевдоожиженный слой, можно по аналогии со свободной за­топленной струей разделить на два участка: начальный (уча­сток постоянной осевой скорости потока) и основной (уча­сток падающей скорости газа). После скоростей в основном Участке струи описывается формулой Шлихтинга [9]:

Поэтому логично предположить, что на начальном участке происходит формирование профиля скоростей от равномерно
распределенного до профиля, описываемого выражением (5). Таким образом, для переходного сечения струи можно запи­

Сать

-Iі (^іт)Т

Где Ьг и Ьг. т — соответственно толшины пограничного слоя газовой зоны и зоны «газ — твердые частицы», определяе­мые по выражениям

Bv= С, "т~ tw л-; (7)

Br_v=c2x. (8)

Подставляя выражения (7) и (8) в уравнение (6) и ре­шая его относительно коэффициента С2, получаем

1

С = С и>)

2— 1 И-.І+ «ви

VO-f^f

Анализ выражения (9) показывает, что коэффициент Сг зависит не только от гидродинамики псевдоожиженного слоя, но и от начальной скорости истечения струи: с увеличением скорости истечения С2 уменьшается. При понижении плотно­сти слоя С2 также уменьшается. В предельном случае, при Рсл=Рг, скорость витания частиц, а следовательно и коэффи­циент С2, принимают значения, равные нулю. Таким образом, выражение (9) находится в полном соответствии с классиче­ской теорией истечения затопленных струй. В таблице пред­ставлены значения' коэффициента С2, рассчитанные по урав­нениям (4) и (9) при различных начальных скоростях исте­чения струи в монодисперсный превдоожиженный слой с диа­метром частиц 1 мм и плотностью 1300 кг/м3. Из данных таб­лицы видно, что при рабочих скоростях истечения газа 150-^300 м/с и порозности слоя є=0,65-^0,80 коэффициент С2, определенный по уравнению (4), имеет среднее значение по отношению к коэффициенту С2, рассчитанному по выра­жению (9).

При этом максимальное и среднее расхождение значений соответственно составляет 32 и 11%. Следует, однако, отме­тить, что при снижении начальной скорости истечения струи расхождение значений коэффициентов, определенных по

Уравнениям (4) и (9), возрастает. Это, на наш взгляд, гово­рит о целесообразности определения коэффициента С2 по уравнению (9).

Для проверки адекватности выражения (9) было прове­дено экспериментальное исследование аэродинамики неогра­ниченной газовой струи в псевдоожиженном слое [6]. Цель исследований заключалась в измерении осевой скорости по­тока в различных сечениях газового факела. Для этого ис­пользовался пневмометрический метод. Чтобы избежать ис­кажения поля скоростей при введении в факел трубки Пито—Прандтля, последняя была изготовлена из медицин­ских игл диаметром 1 мм.

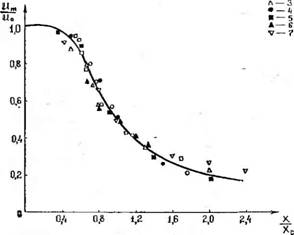
Результаты опытов представлены на рисунке в виде гра­фических зависимостей безразмерной осевой скорости газа от безразмерного расстояния (хс — расстояние от сопла до точки, в которой скорость струи в два раза меньше началь­ной). Кривая этого рисунка рассчитана с помощью матема­тической модели струи [6, 7] с использованием выражения (9), точки — экспериментальные данные, полученные при ис­следовании процесса истечения неограниченной струи в псев­доожиженный слой частиц риса и гранул сульфата аммония, а также заимствованные из диссертаций Минаева и Листов - цевой, исследовавших развитие изотермической [8] и неизо­термической [10] струй в псевдоожиженном слое частиц алюмосиликатного катализатора.

Удовлетворительное совпадение расчетного и эксперимен­тального профилей безразмерной осевой скорости струи под-

Тверждает справедливость уравнения (9) и показывает воз­можность использования его для практических расчетов. Кроме того, интересно отметить, что предложенный метод определения коэффициента С2 может быть с достаточной точностью применен и при расчете неизотермической струи. Последнее обстоятельство является весьма ценным с точки зрения практических расчетов процессов грануляции, так как при осуществлении процесса гранулирования минеральных удобрений в псевдоожиженном слое всегда имеет место ис­течение неизотермической газожидкостной струи.